透鏡體對尾礦壩安全性影響的參數敏感性分析

袁維，白冰，李小春，汪海濱

(中國科學院武漢巖土力學研究所，巖土力學與工程國家重點實驗室，湖北 武漢，430071)

尾礦壩是尾礦庫構筑物的主體，影響其穩定性的因素較多，大致與以下幾個方面相關[1]：壩體內浸潤線高度、沉積灘長度、尾礦砂密實度、尾礦沉積層的抗剪強度、堆積壩的高度、庫水位的高度、排洪系統的有效性等。在理想狀態下，在礦漿由壩前向庫內流動的過程中，由于挾砂能力的變化，礦漿中的尾礦根據其粒徑按粗、中、細、泥依次沉積，形成尾礦沉積灘，此沉積灘構成尾礦堆積壩的壩體[1-3]。然而，在向尾礦庫排放尾礦時，由于受尾礦粒度、礦漿濃度、流速、排放方法、尾礦池水位及大氣降水等諸多因素影響，尾礦在庫中的沉積過程非常復雜，尾礦堆積壩在形成的過程中會含有許多夾層，以透鏡體的形式存在，在空間上表現出不連續性，破壞了堆積壩的正常沉積規律，給壩體帶來安全隱患，影響主要表現在以下 2個方面：(1) 相互穿插以及不同大小、不同位置和不同形狀的透鏡體改變了壩體內的滲透路徑；(2) 大量的透鏡體影響了沉積層土體的抗剪強度參數以及變形參數等[4-7]。因此，在對壩體進行穩定性評價時，不能忽略透鏡體對其穩定性的影響。在透鏡體所具有的眾多影響因素中，存在一些關鍵因素值得注意，在工程實踐中，應重點研究這些關鍵因素對尾礦壩安全性的影響。本研究擬把浸潤線深度、壩頂位移和安全系數作為尾礦壩穩定性的3個評價指標，擬把透鏡體參數分為幾何參數(透鏡體面積比率、上下位置、形狀)和材料參數(滲透系數、泊松比、鄧肯-張模型7個參數)，采用耦合正交試驗設計法與熵權決策法對透鏡體進行參數敏感性分析，尋求透鏡體對壩體穩定性影響的關鍵因素，以便為尾礦壩安全性分析與評價提供參考。

1 正交試驗設計法與熵權決策法的基本原理

1.1 正交試驗設計法

正交試驗設計[8-10]是用于多因素試驗的一種方法，它是從全面試驗中挑選出部分有代表性的點進行試驗，具有很高的效率。試驗中把要考察的對象稱為指標，把有可能影響指標結果的因子稱為因素，把每個因素在試驗中要比較的具體條件稱為水平。

設A，B，…表示不同的因素，r表示各因素水平數；Ai表示因素A的第i水平(i=1, 2, …, r)；Xij表示因素j的第i水平的值(i=1, 2, …, r；j=A，B，…)。在Xij下進行試驗得到因素j第i水平的試驗結果指標Yij，Yij是服從正態分布的隨機變量。在Xij下做n次試驗得到n個試驗結果，分別為Yijk(k=1, 2, …, n)，則得到如下計算式：

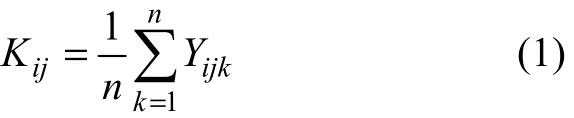
式中：Kij表示因素j在i水平下的統計參數。

評價因素顯著性的參數為極差Rj，其計算公式為

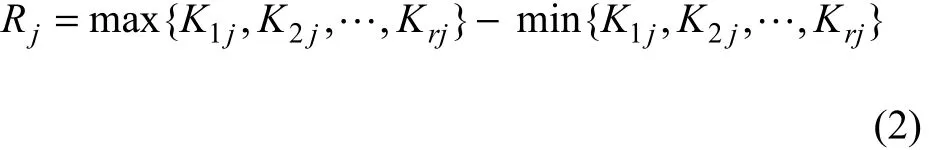
極差越大說明該因素的水平改變對試驗結果影響也越大，因此可根據極差的大小把各個因素對指標的影響程度排序。

1.2 熵權決策法

信息熵可以用來度量不同指標的信息效用值，采用熵權決策法[11-14]可以使評價結果更為合理。具體計算過程如下：

(1) 假定評價指標有m個，每個評價指標的影響因子有n個，則每個評價指標的影響因子可構成判斷矩陣

(2) 對判斷矩陣進行歸一化處理，從而得到歸一化矩陣B，B的元素為：

式中：rmin和rmax分別表示同一影響因子下不同評價指標中的最小和最大值。

(3) 按照傳統的熵的概念，定義影響因子的熵為：

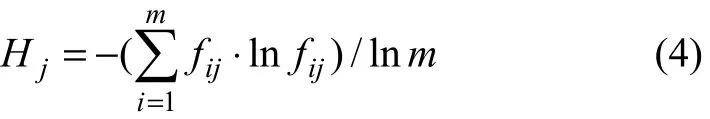
式中：將fij定義為

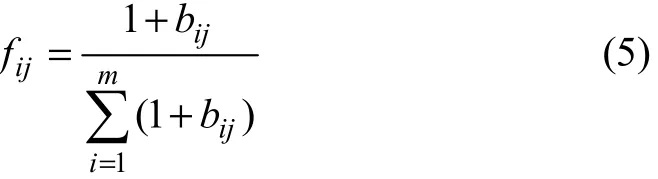
因此，第j個指標的熵權Xj定義為

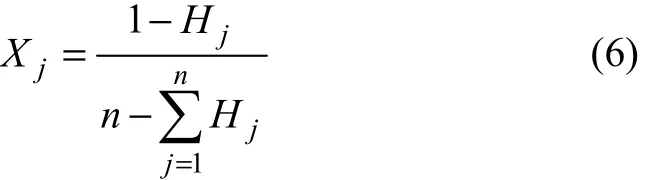
根據上述定義，就可以把熵權決策法原理應用到尾礦壩的安全評價中來，各影響因子的熵權值具有以下意義：

(1) 被評價指標在影響因子j上的熵值較小、熵權較大時，說明該影響因子對評價指標的影響較大，各評價指標在該影響因子上有明顯的差異，應作為重點考察對象。

(2) 影響因子的熵權值滿足0≤Xj≤1，且同時滿足

(3) 根據影響因子熵權值，可判斷各個影響因子對評價指標影響的敏感程度。

(4) 考慮熵權后的歸一化判斷矩陣A為

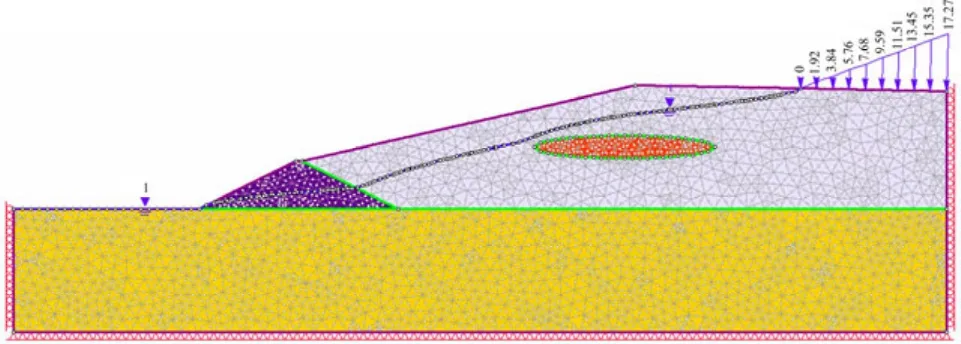
圖1 網格模型圖Fig.1 Picture of grid model

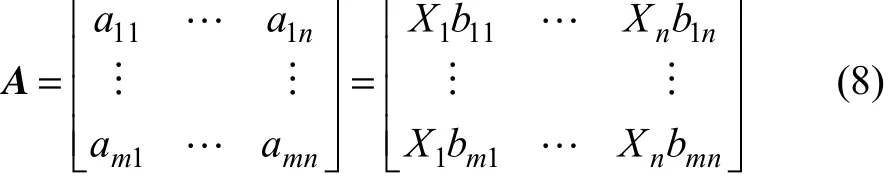
(5) 理想點P為：P=(p1, p2, …, pn)，式中pj為A中每列的最大值。

(6) 被評價對象與理想點的貼近度為

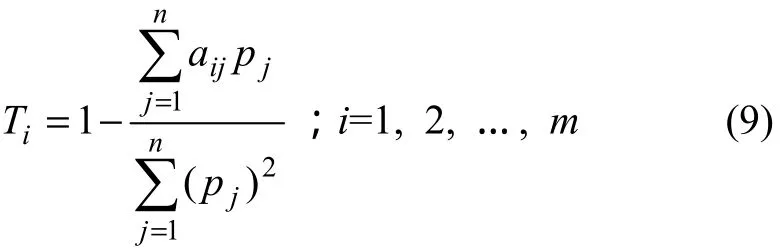
貼近度越小，則說明該評價指標越優。

2 計算模型與參數的選取

為了研究透鏡體對尾礦壩穩定性的影響，選取某尾礦壩的主壩剖面為研究對象。該尾礦壩壩體材料主要為尾粉砂，透鏡體為尾粉質黏土，初期壩為透水堆石壩，壩基為灰巖。初期壩內外坡比為1:2，初期壩高為29 m，堆積壩平均坡比為1:5.5，壩高為75 m，沉積灘平均坡率為 2%，計算正常水位情況在自重荷載作用下的穩定性。計算模型及網格如圖1所示。

透鏡體與堆積壩采用鄧肯-張 7參數模型[15]，初期壩與壩基破壞準則采用摩爾庫倫模型，基準計算參數如表1所示。

3 透鏡體幾何參數敏感性分析

透鏡體對壩體安全性產生影響的幾何參數可歸結為以下4個因素：透鏡體在壩體剖面中的面積比率(A)、透鏡體的上下位置(B)、透鏡體的左右位置(C)和透鏡體的形狀(D)。4個因素的不同水平如下所述：

A表示剖面中透鏡體面積除以壩體總面積，取5%、12.5%、20% 3個水平值。

B表示透鏡體在壩體中的垂直位置，取上(透鏡體靠近沉積灘)、中(透鏡體處于沉積灘表面與基巖面的正中部)和下(透鏡體靠近基巖)3個水平值。

C表示透鏡體在壩體中的水平位置，取左(透鏡體靠近壩體坡面)、中(透鏡體處于坡面與右端的正中部)和右(透鏡體靠近數值模型的最右端)3個水平值。

D表示透鏡體長軸與短軸的比值(透鏡體用橢圓來描述)取12，8和4共3個水平值。

綜上所述，選擇 L9(34)正交表構建試驗方案，表示用該正交表可安排4個因素，每個因素均為3水平，總共要做9次試驗。試驗方案表如2所示。

采用有限元法對上述9個試驗進行數值模擬，把計算結果進行極差分析，3個評價指標的不同影響因子的極差分別如表3所示。

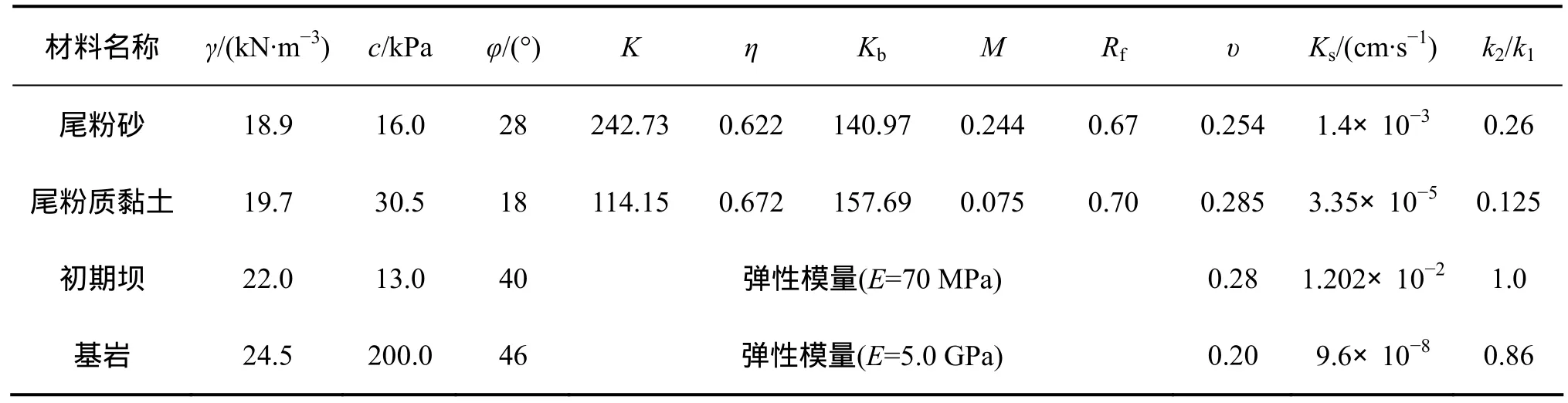
表1 材料基準參數Table 1 Parameters of material benchmarks

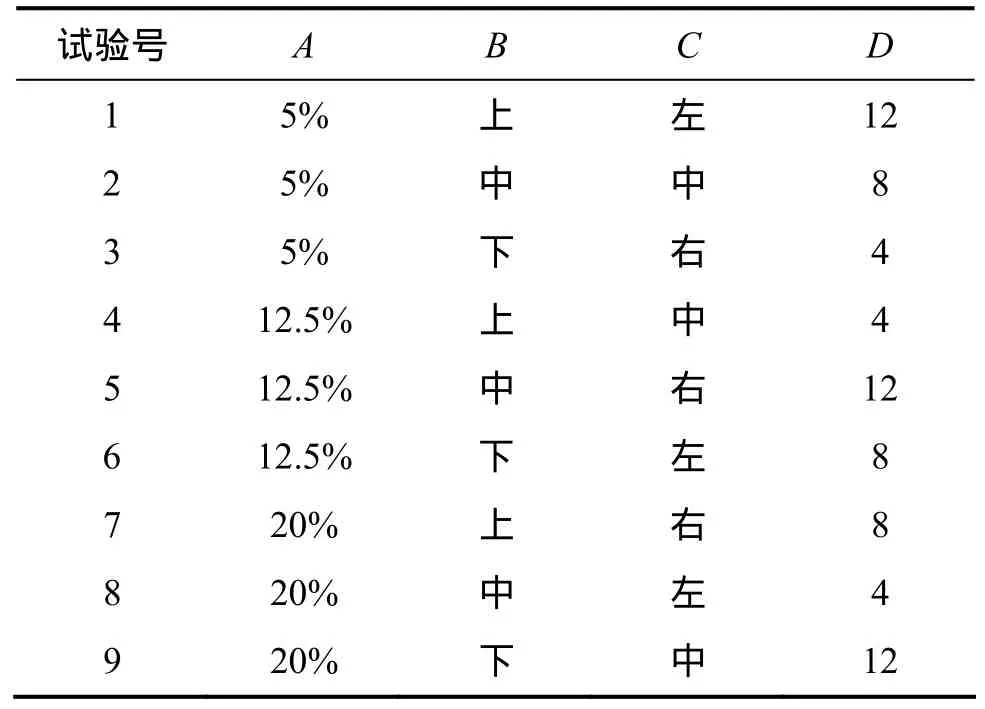
表2 幾何敏感性分析試驗方案Table 2 Table of experiment program for analysis of geometrical sensitivity

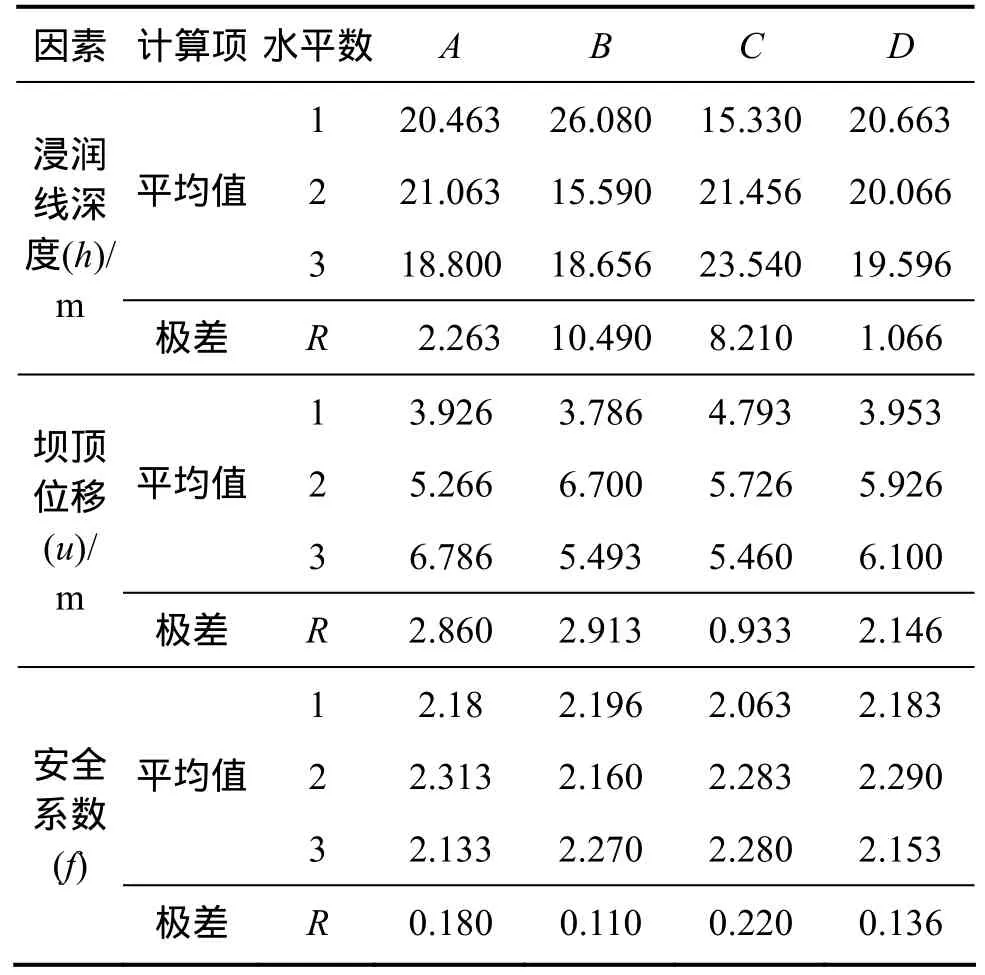
表3 幾何參數敏感性分析極差計算結果Table 3 Results of range analysis of geometrical parameter sensitivity

由表3可得出如下結論。

(1) 對評價指標浸潤線深度而言，4個因子的極差排序如下：

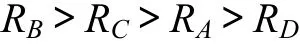
其中：RB和 RC比 RA和 RD大得多，這表明透鏡體的垂直位置和水平位置比透鏡體的形狀和面積率對浸潤線深度的影響要大得多，而垂直位置對其的影響最大，透鏡體形狀對其影響最小。將4個因素的3水平平均浸潤線深度繪于同一圖上，如圖2所示。

由圖2可以看出：在當前因素水平下，浸潤線深度最淺的因素水平組合應該是A3B2C1D3，即面積比率取20%，垂直位置取中部，水平位置取左部，長短軸比值取4。

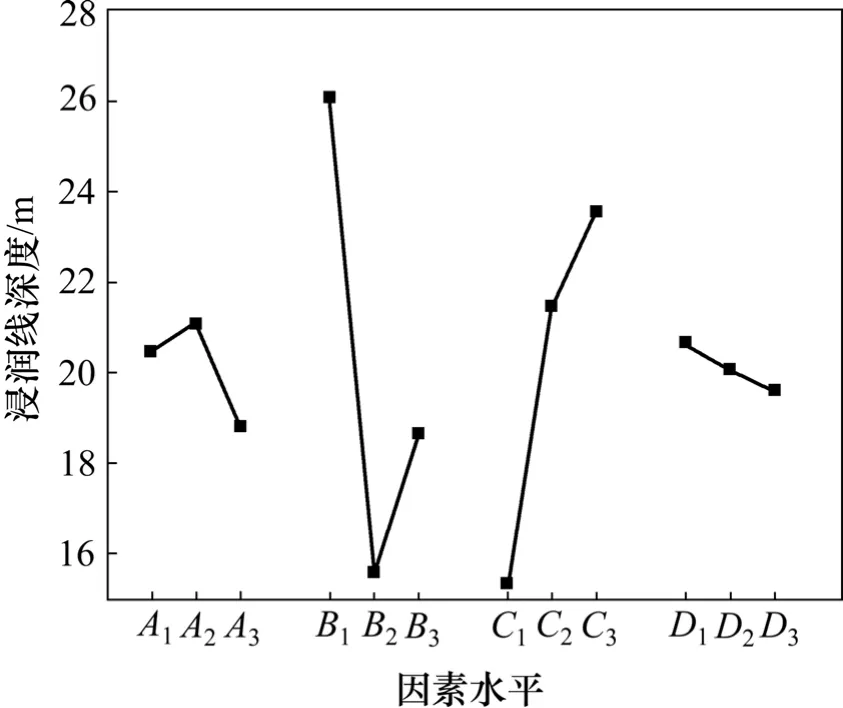
圖2 浸潤線深度與4因素關系圖Fig.2 Graph for relation between depth of saturation line and four elements

(2) 對評價指標壩頂位移而言，4個因子的極差排序如下：

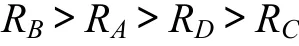
這表明垂直位置對壩頂位移影響最大，透鏡體面積比率次之，水平位置對壩頂位移的影響最小。將 4個因素的3水平平均壩頂位移繪于同一圖上，如圖3所示。

由圖3可以看出：在當前因素水平下，壩頂位移最大的因素水平組合應該是A3B2C2D3，即面積比率取20%，垂直位置取中部，水平位置取中部，長短軸比值取 4。但是，壩頂位移在面積比率和長短軸比值的影響下呈單調變化趨勢，意味著隨著面積比率的增大和長短軸比值的減小，壩頂位移有可能存在繼續增大的趨勢。

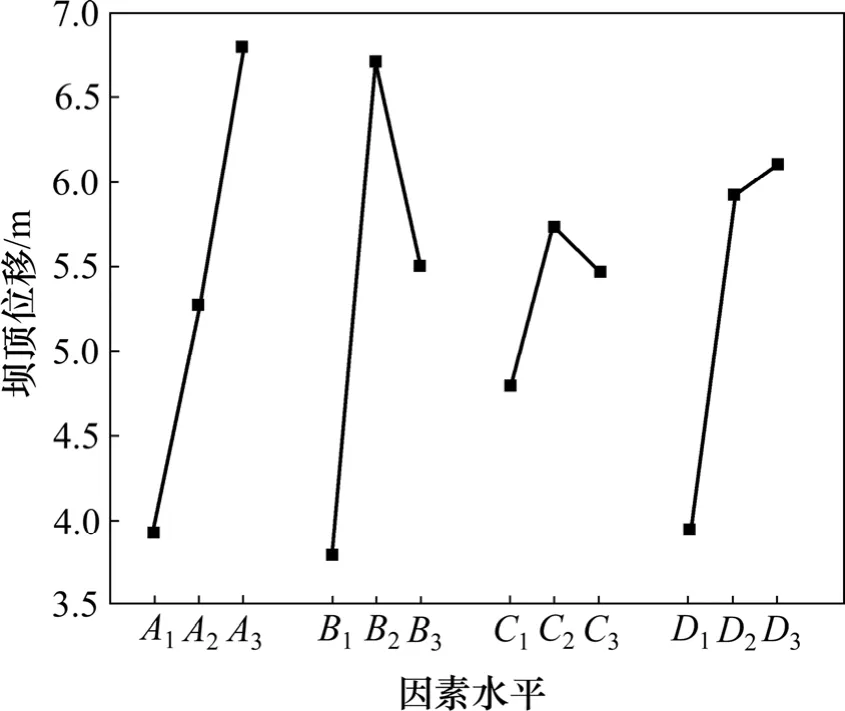
圖3 壩頂位移與4因素關系圖Fig.3 Graph for relation between displacement of dam crest and four elements

(3) 對評價指標安全系數而言，4個因子的極差排序如下：

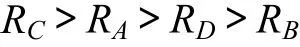
這表明水平位置對安全系數影響最大，透鏡體面積比率次之，垂直位置影響最小。將4個因素的3水平平均安全系數繪于同一圖上，如圖4所示。

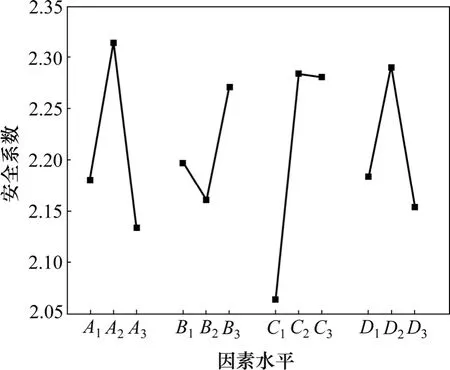
圖4 安全系數與4因素關系圖Fig.4 Graph for relation between safety factor and four elements

由圖4可以看出：在當前因素水平下，安全系數最小的因素水平組合是A3B2C1D3，即面積比率取20%、垂直位置取中部、水平位置取左部、長短軸比值取4。

對表3分析可知：在當前因素水平下，雖然3種評價指標的最不利因素水平組合極為接近(浸潤線深度與安全系數為 A3B2C1D3、壩頂位移為 A3B2C2D3)，但是，對不同評價指標而言，其各自的顯著影響因子卻不盡相同。因此，需要綜合以上3個評價指標的幾何影響因子，找出盡量能同時反映3個指標的顯著幾何影響因子，并且優選出在幾何敏感性分析條件下最佳的評價指標。本研究采用熵權決策法進行求解，計算結果如表4和表5所示。

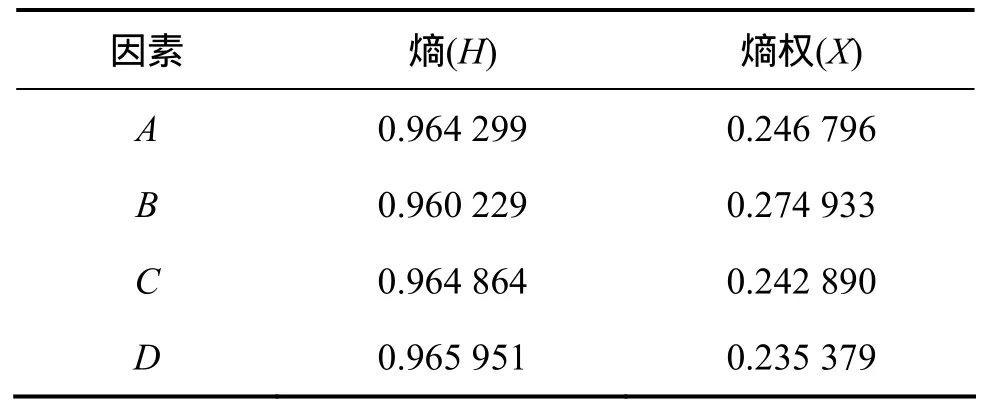
表4 信息熵與熵權值Table 4 Comentropy and entropy weight

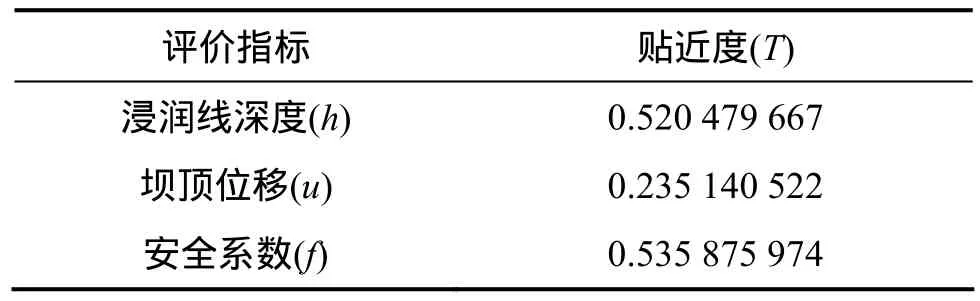
表5 3個評價指標的貼近度Table 5 Approach degree of three evaluation factors

由表4可得：

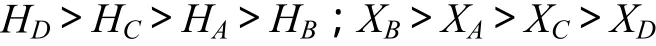
根據熵權決策法原理，這表明4個影響因子中，垂直位置對評價指標的影響最大，透鏡體面積比率次之，長短軸比值對評價指標的影響最小。

由表5可得：

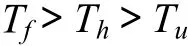
根據熵權決策法原理，表明透鏡體的幾何因子產生的影響最主要體現在壩頂位移上。

4 透鏡體材料參數敏感性分析

擬針對以下9個參數進行透鏡體參數敏感性進行分析：滲透系數(Ks)、剛度參數(K，η，Kb，m，Rf)、泊松比(υ)、強度參數(c，φ)。為表示方便，透鏡體 9個參數與 A～I共 9個字母依次呈對應關系，如表 6所示。

表6 參數與字母對應關系Table 6 Corresponding relationship between factors and letters

假設“透鏡體參數/周圍土體參數=k”，把 k作為基準值，通過調整透鏡體參數構建以下4個因素水平：

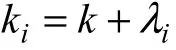
式中：水平i=1, 2, 3, 4；iλ(i=1, 2, 3, 4)分別為-20%,-10%, 10%, 20%；ki表示調整后的參數比值。

綜上所述，選擇L32(49)正交表構建試驗方案，表示用該正交表可安排9個因素，每個因素均為4水平，總共要做32次試驗。

采用有限元法對上述32個試驗進行數值模擬，把計算結果進行極差分析，3個評價指標的不同影響因子的極差分別如表7所示。

由表7可得出如下結論：

(1) 對評價指標浸潤線深度而言，9個因子的極差排序為

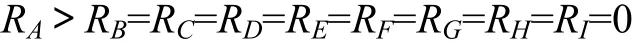
其中：只有RA≠0，其他各項極差皆為0，表明只有滲透系數對浸潤線深度產生影響。將9個因素的4水平平均浸潤線深度繪于同一圖上，如圖5所示。

由圖5可以看出：在當前因素水平下，浸潤線深度最淺的因素水平組合是“A1+任意其他因素水平”。浸潤線深度隨著透鏡體滲透系數增大而單調增大，這表明，透鏡體滲透系數越大，則浸潤線深度越大，壩體越安全。

(2) 對評價指標壩頂位移而言，9個因子的極差排序如下：

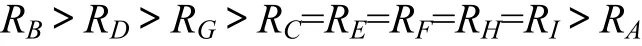
將9個因素的4水平平均壩頂位移繪于同一圖上，如圖6所示。

9個因子對壩頂位移均產生一定程度的影響，其中ks產生的影響最小，K產生的影響最大。由圖6可見：隨著 K增大，壩頂位移呈單調減小趨勢，其他參數對壩頂位移有一定的影響，但遠小于 K對其的影響。

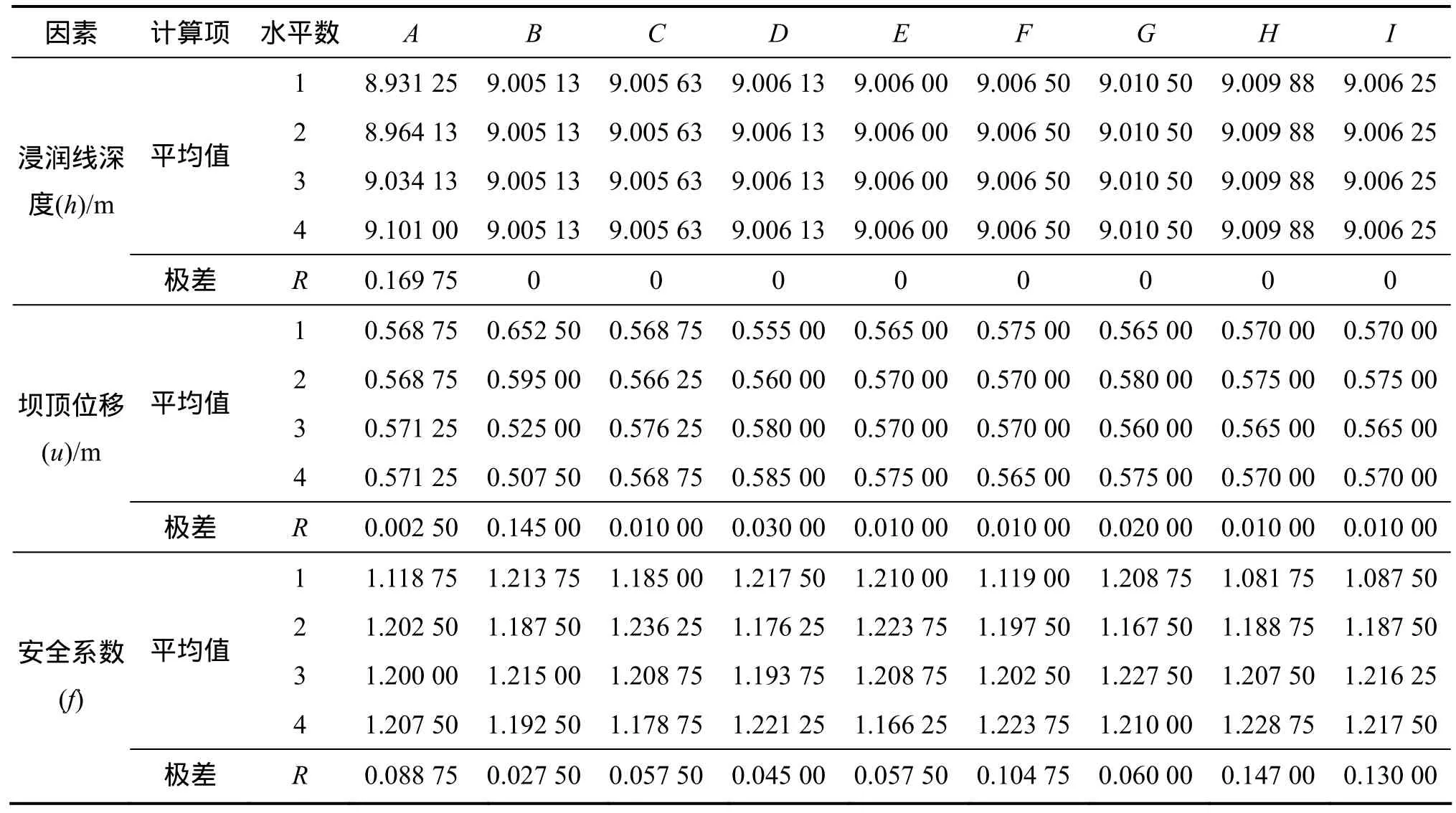
表7 材料參數敏感性分析極差計算結果Table 7 Results of range analysis for analysis of material parameter sensitivity

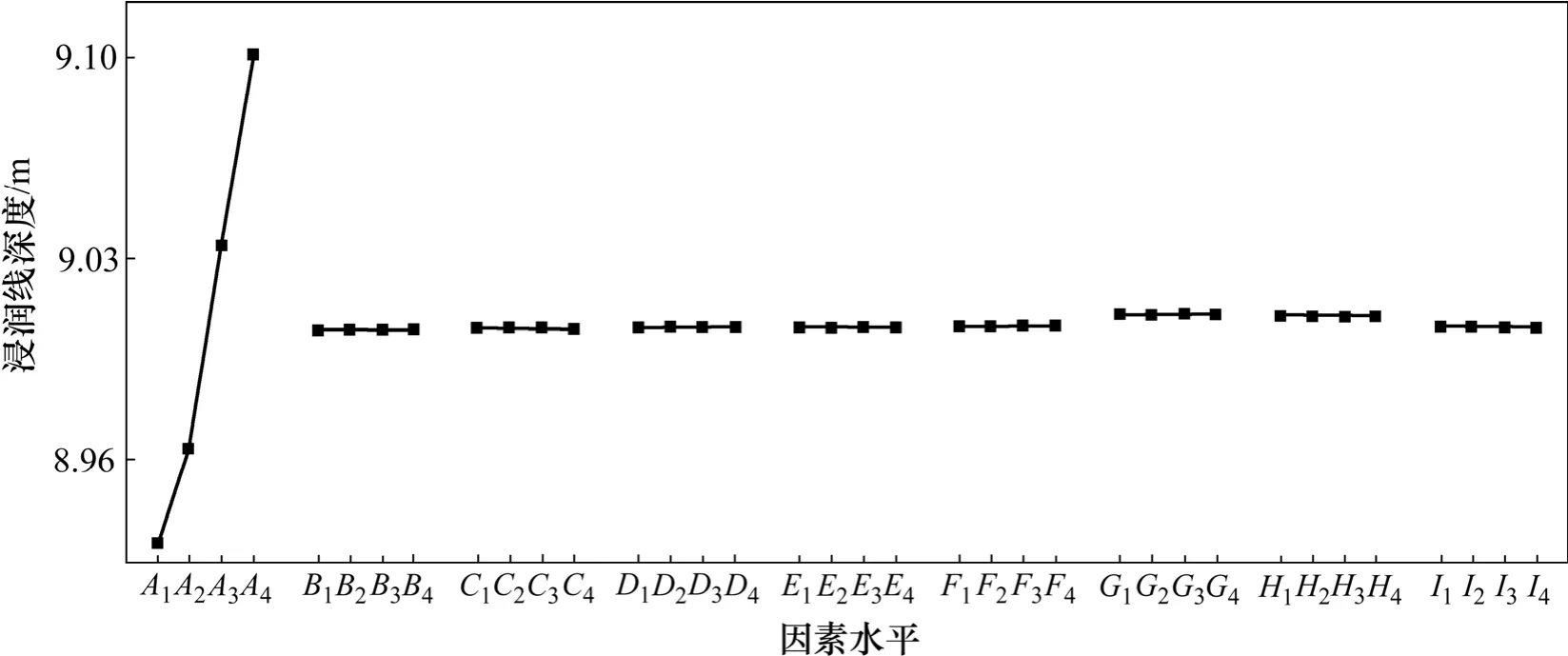
圖5 浸潤線深度與9因素關系圖Fig.5 Graph of relation between depth of saturation line and nine elements

(3) 對評價指標安全系數而言，9個因子的極差排序如下：

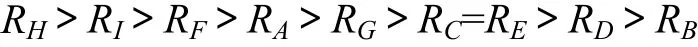
將9個因素的4水平平均安全系數繪于同一圖上，如圖7所示。

由圖7可見：9個因子對安全系數皆有一定程度的影響，其中強度參數c與φ對安全系數的影響最明顯，ks與Rf次之，其余參數則對安全系數的影響不太明顯。由圖 7可以看出：安全系數是 c，φ，Rf和 ks的單調遞增函數，此4個因素水平值越大，則安全系數越大。

由表7可見：3個評價指標的顯著影響因子各不相同，表現出的規律亦存在一定差異。因此，需要綜合以上3個評價指標的參數影響因子，找出盡量能同時反映3個指標的顯著參數影響因子，并且優選出在參數敏感性分析條件下最佳的評價指標。本研究采用熵權決策法進行求解，計算結果如表8和表9所示。由表8可得：

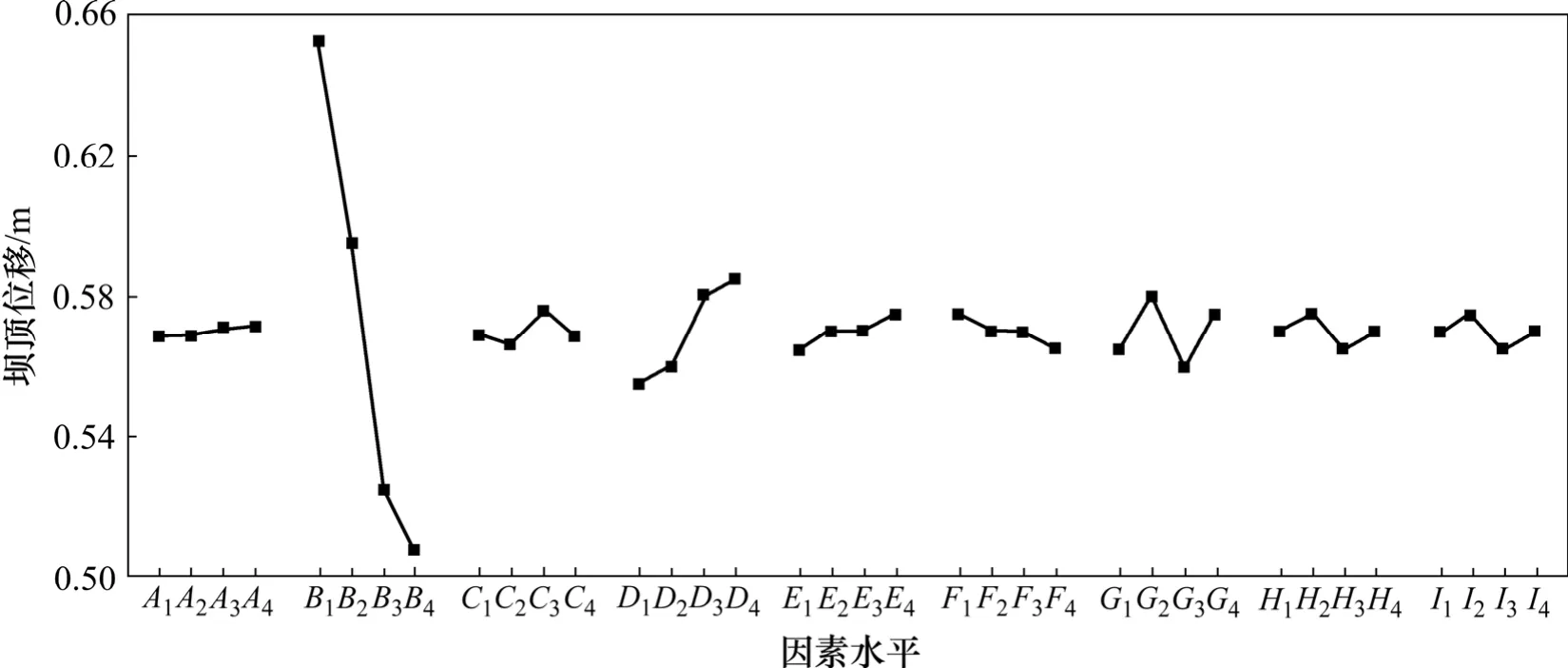
圖6 壩頂位移與9因素關系圖Fig.6 Graph of relation between displacement of dam crest and nine elements

圖7 安全系數與9因素關系圖Fig.7 Graph of the relation between the safety factor and nine elements

表8 信息熵與熵權值Table 8 Comentropy and entropy weight

表9 3個評價指標的貼近度Table 9 Approach degree of three evaluation factors

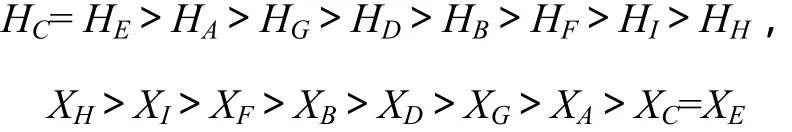
根據熵權決策法原理，表明c與φ是顯著影響因子，而η與m則對評價指標的影響最小，其他影響因子亦有一定程度的影響。

由表9可得：

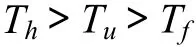
根據熵權決策法原理，表明透鏡體的參數因子產生的影響最主要體現在安全系數上。

5 補充實驗

由前面分析可知：透鏡體的垂直位置、面積比率、c和φ是透鏡體4個對壩體穩定性影響較大的參數，為了進一步明晰其各自對壩體穩定性的影響，作進一步的數值實驗。

選取壩頂位移和安全系數作為評價指標，透鏡體垂直位置、面積比率、c和φ作為影響因子的3水平如下所述：A為垂直位置(上、中、下)；B為面積比率(5%，12.5%，20%)；C為黏結力(k-20%，k，k+20%)；D為摩擦角(k-20%，k，k+20%)。式中：k的取值同于第4節中的取值。

由此可選取 L9(34)正交表構建實驗方案，正交表如表10所示，2個評價指標不同影響因子的極差如表11所示。壩頂位移和安全系數與影響因子關系圖如圖8和圖9所示。

由表11可見：壩頂位移與安全系數的極差分析結果相同：

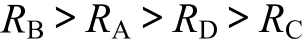
這表明：此處4個影響因子對這2個指標的影響呈現相同的規律，即面積比率對其影響最大，垂直位置次之，黏結力影響最小。

由圖8可見：透鏡體的c和φ對壩頂位移影響較小，遠小于垂直位置與面積比率的影響；另外，隨著面積的增大，壩頂位移增大，而對于垂直位置而言，當透鏡體處于剖面中部時，壩頂位移最大。

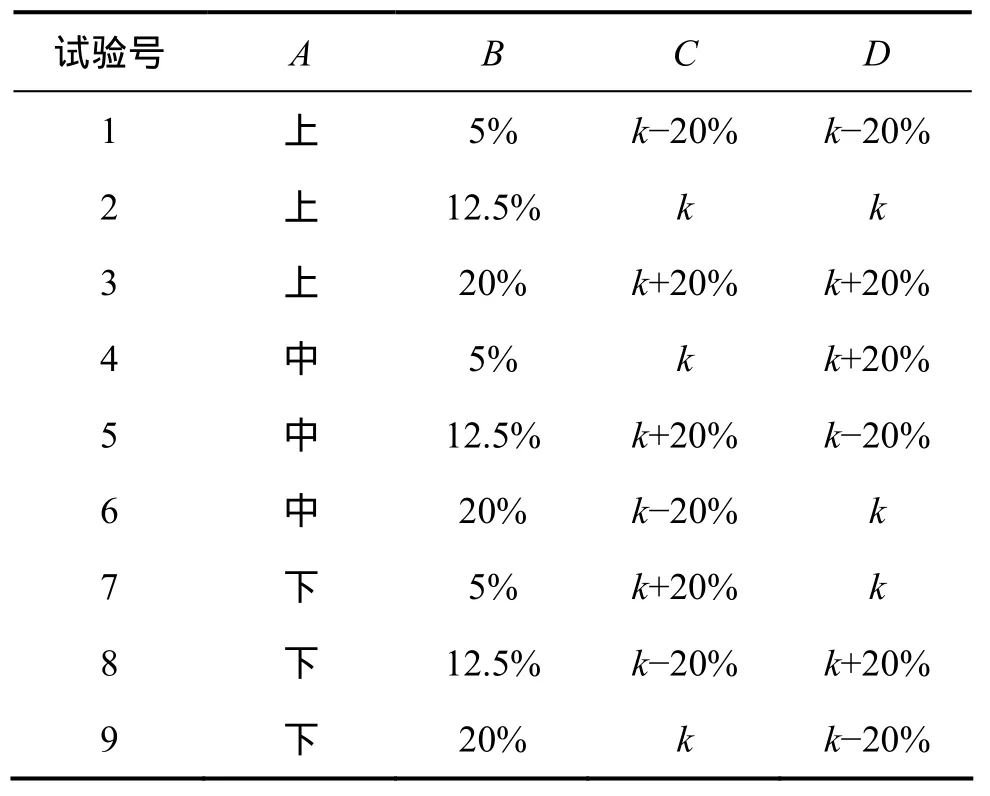
表10 補充正交試驗方案表Table 10 Table of supplementary experiment program

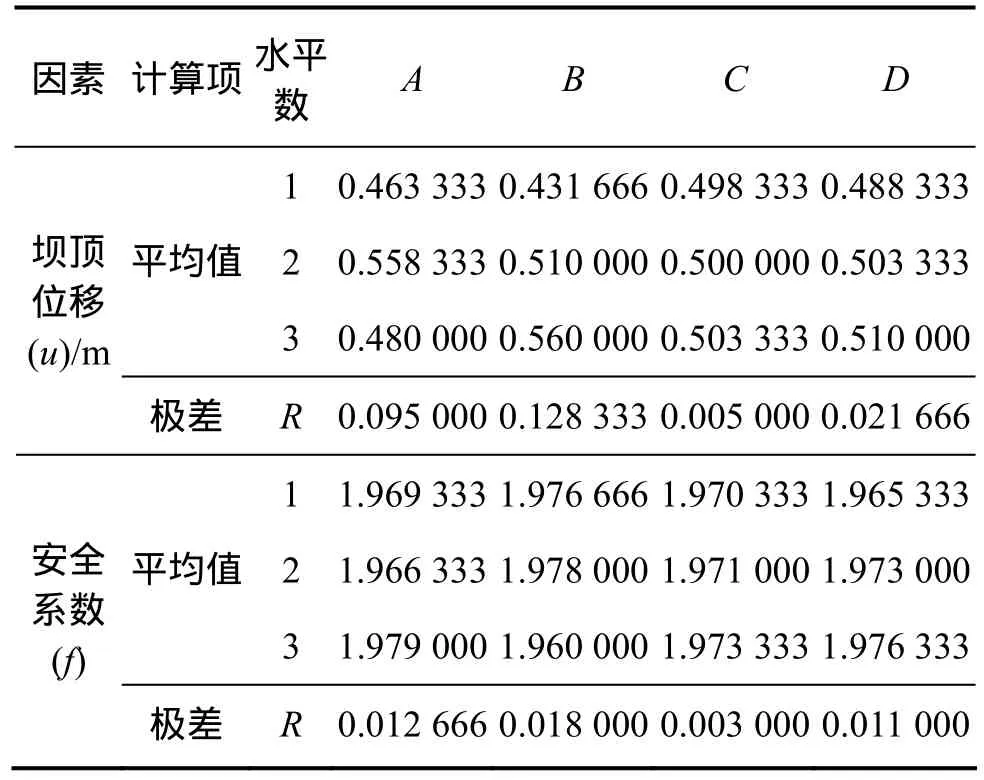
表11 補充方案敏感性分析極差計算結果Table 11 Results of range analysis for supplementary sensitivity analysis

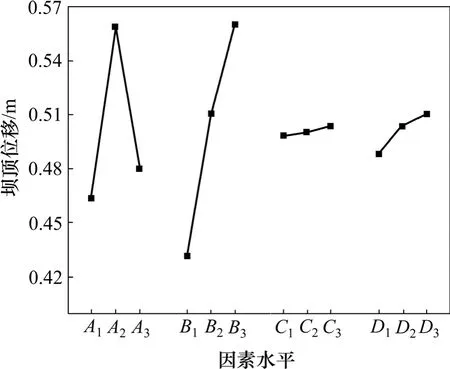
圖8 壩頂位移與4因素關系圖Fig.8 Graph of relation between displacement of dam crest and four elements

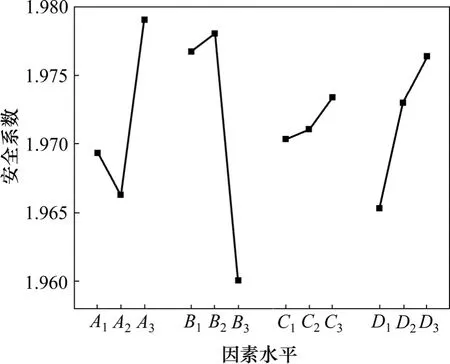
圖9 安全系數與4因素關系圖Fig.9 Graph of relation between safety factor and four elements

由圖9可見：透鏡體的c和φ對安全系數的影響仍小于垂直位置與面積比率的影響，且隨著c和φ的增大，壩體的安全系數有一定程度的提高；另外，在趨勢上，面積比率越大，安全系數越小，而對垂直位置而言，安全系數最小的位置亦為剖面中部。

6 結論

(1) 評價壩體穩定性的指標較多，透鏡體的幾何參數產生的影響主要體現在壩頂位移上，材料參數產生的影響主要體現在安全系數上，幾何參數產生的影響要明顯大于材料參數的影響。

(2) 幾何參數中，2個最大的影響因子是透鏡體的垂直位置和面積比率；材料參數中，2個最大的影響因子是透鏡體的c和φ。

(3) 針對 2個影響最大的幾何參數而言，透鏡體面積比率越大，則浸潤線深度越淺，壩頂位移越大，安全系數越小，壩體安全性越不利；透鏡體處于頂部時壩體安全性最好，處于底部時安全性次之，而處于中部時，壩體安全性最差；另外，針對透鏡體水平位置而言，透鏡體處于左部靠近壩體前緣時，壩體安全性最差，處于中部時次之，處于右部時最好。

(4) 針對2個影響最大的材料參數而言，c和φ越大，壩體安全性越好。另外，滲透系數 Ks與破壞比Rf亦對安全系數有一定程度的影響，Ks越小，則浸潤線深度越淺，故安全系數越小；Rf越小，則表明土體的抗壓強度越難達到極限值，故安全系數越小。

(5) 上述敏感性分析結果具有重要的工程意義。首先，尾礦壩在放礦時，盡量把尾礦砂往沉積灘方向疏排，盡量讓透鏡體遠離壩體前緣而在壩體后緣沉積；其次，在壩體加高過程中，要處理好灘面的尾礦砂，以免在壩體上緣產生過多透鏡體；此外，在判斷壩體的穩定性時，安全系數不應作為唯一的評價指標，建議結合壩頂位移值綜合評價其穩定性。在對壩體進行監測時，要重視對壩頂及壩體前緣各處的位移監測。

[1] 陳守義. 淺議上游法細粒尾礦堆壩問題[J]. 巖土力學, 1995,16(3): 70-76.CHEN Shouyi. Some superficial views on the problem of building fine grain tailings fill dams by means of up-stream method[J]. Rock and Soil Mechanics, 1995, 16(3): 70-76.

[2] 李夕兵, 蔣衛東, 賀懷建. 尾礦堆積壩透鏡體分布狀態研究[J]. 巖土力學, 2004, 25(6): 947-949.LI Xibing, JIANG Weidong, HE Huaijian. Study on distributing state of lenticle in tailings fill dam[J]. Rock and Soil Mechanics,2004, 25(6): 947-949.

[3] 王躍飛, 徐志勝, 董隴軍. 尾礦壩穩定性分析的模糊隨機可靠度模型及應用[J]. 巖土工程學報. 2008, 30(11): 1600-1605.WANG Yuefei, XU Zhisheng, DONG Longjun. Stability model of tailing dams based on fuzzy random reliability[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(11): 1600-1605.

[4] 蔣衛東. 尾礦壩非線性系統混沌與安全研究[D]. 長沙: 中南大學資源與安全工程學院, 2003: 54-55.JIANG Weidong. Research on chaos and safety of nonlinear system for tailings dam[D]. Changsha: Central South University.School of Resource and Safety Engineering, 2003: 54-55.

[5] 胡明鑒, 陳守義, 郭愛國, 等. 某上游法尾礦壩抗滑穩定性淺析[J]. 巖土力學, 2003, 23(增刊): 254-258.HU Mingjian, CHEN Shouyi, GUO Aiguo, et al. Opinions on the gangue-dam anti-slide stability analysis[J]. Rock and Soil Mechanics, 2003, 23(supplement): 254-258.

[6] 顏學軍. 上游法尾礦堆筑壩壩體沉積規律探討[J]. 稀有金屬與硬質合金, 2008, 36(2): 54-58.YAN Xuejun. Investigation on the depositing law of tailings dam by upstream damming[J]. Rare Metals and Cemented Carbides,2008, 36(2): 54-58.

[7] 路榮博, 王濤. 上游法尾礦庫潰壩事故致因分析及安全管理技術研究[J]. 長江科學院院報, 2009, 26(增刊): 112-117.LU Rongbo, WANG Tao. Safety management technique and accident causing analysis of dam failure in upstream tailings pond[J]. Journal of Yangtze River Scientific Research Institute,2009, 26: 112-117.

[8] 張旭輝, 龔曉楠, 徐日慶. 邊坡穩定影響因素敏感性正交法計算分析[J]. 中國公路學報, 2003, 16(1): 36-39.ZHANG Xuhui, GONG Xiaonan, XU Riqing. Orthogonality analysis method of sensitivity on factor of slope stability[J].China Journal of Highway and Transport, 2003, 16(1): 36-39.

[9] 田浩, 王宇, 余宏明. 基于耦合分析法的邊坡穩定性影響因素敏感性研究驗證[J]. 安全與環境工程, 2011, 18(2): 112-115.TIAN Hao, WANG Yu, YU Hongming. Coupled analysis of slope stability based on the sensitivity affecting factors[J]. Safety and Environmental Engineering, 2011, 18(2): 112-115.

[10] 方開泰, 馬長興. 正交與均勻試驗設計[M]. 北京: 科學出版社, 2001: 35-50.FANG Kaitai, MA Changxing. Design of experiment based on orthogonality and orthogonality[M]. Beijing: Science Press,2001: 35-50.

[11] 閆文周, 顧連勝. 熵權決策法在工程評標中的應用[J]. 西安建筑科技大學學報: 自然科學版, 2004, 36(1): 98-100.YAN Wenzhou, GU Liansheng. Application of the method of entropy proportion in the engineering mark[J]. Journal of Xi’an University of Architecture and Technology: Natural Science Edition, 2004, 36(1): 98-100.

[12] 黃書嶺, 馮夏庭, 張傳慶. 巖體力學參數的敏感性綜合評價分析方法研究[J]. 巖石力學與工程學報, 2008, 27(增 1):95-100.HUANG Shuling, FENG Xiating, ZHANG Chuanqing. Study of method of comprehensive evaluation for parameters of constitutive model of rock mass[J]. 2008, 27(supplement 1):95-100.

[13] 馮夏庭, 周輝. 雅礱江錦屏二級水電站招標設計階段引水隧洞圍巖穩定性及結構設計研究報告[R]. 武漢: 中國科學院武漢巖土力學研究所, 2006.FENG Xiating, ZHOU Hui. Study on stability of surrounding rock and structure design of hydropower tunnels on stage of bidding design for Jinping-Ⅱ hydropower station of Yalong River[R]. Wuhan: Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, 2006.

[14] 蘇國韶, 馮夏庭, 江權, 等. 高地應力下地下工程穩定性分析與優化的局部能量釋放率新指標研究[J]. 巖石力學與工程學報, 2006, 25(12): 2453-2460.SU Guoshao, FENG Xiating, JIANG Quan, et al. Study on new index of local energy release rate for stability analysis and optimal design of underground rock mass engineering with high geostress[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(12): 2453-2460.

[15] 鄭潁人, 孔亮. 巖土塑性力學[M]. 北京: 中國建筑工業出版社, 2010: 233-237.ZHENG Yingren, KONG Liang. Geotechnical plastic mechanics[M]. Beijing: China Architecture and Building Press,2010: 233-237.

[16] 顏永國, 陳建. 基于條分模式的邊坡可靠度近似計算方法[J].防災減災工程學報, 2010, 30(3): 315-319.YAN Yongguo, CHEN Jian. Approximate calculation method of slope reliability degree based on slide mode[J]. Journal of Disaster Prevention and Mitigation Engineering, 2010, 30(3):315-319.

[17] 彭振斌, 李俊, 彭文祥. 基于bishop條分法的邊坡可靠度應用研究[J]. 中南大學學報: 自然科學版, 2010, 31(3): 668-672.PENG Zhenbin, LI Jun, PENG Wenxiang. Application anslysis of slope reliability based on bishop analytical method[J]. Journal of Central South University: Science and Technology, 2010,31(3): 668-672.

[18] 黃高峰, 李宗利, 眸聲遠. Hoek-Brown準則參數在邊坡工程中的敏感性分析[J]. 巖土力學, 2009, 30(7): 2163-2167.HUANG Gaofeng, LI Zongli, MOU Shengyuan. Sensitivity analysis of Hoek-Brown failure criterion parameters on slope projects[J]. Rock and soil Mechanics, 2009, 30(7): 2163-2167.