基于多目標規劃的礦車調度優化模型

馮陽陽

（西安外事學院工學院 陜西 西安 710077）

鋼鐵工業是國家工業的基礎之一，鐵礦是鋼鐵工業的主要原料基地。許多現代化鐵礦是采用露天開采形式，其生產主要是由各種大型采礦設備間的配合來完成的。隨著露天礦產量規模的不斷擴大及設備大型化、機械化、自動化程度的不斷提高，采運成本占礦山生產成本的比例也越來越高，優化車隊運行、準確執行生產計劃，以提高礦山產量，節約費用，取得較高經濟效益顯得尤為重要。可以說，在采運過程中運輸組織方案的優劣，會直接影響到鋼鐵工業的經濟效益。也就是說，提高這些大型采礦和運輸設備的利用率是增加露天礦經濟效益的首要任務。因此，如何通過合理的調度組織來提高這些露天卡車的工作效率就成為提高露天礦業經濟利潤的重中之重。通常來說，交通對于經濟的作用主要是良好的交通狀況帶來了機動化程度的增長從而節約了運輸時間、降低了運費、降低了產品的成本、促進了物資的流通、帶動了地區間的交流等。

露天礦是在基建和生產過程中逐漸形成的。基建時期的任務是建立供電供水系統及建立運輸干線，修建選礦廠、排土場及機修廠等主要構筑物和設施，以及完成投產時所必需的采準和剝離工程量。在生產過程中，為了完成計劃的年礦石生產任務，必須按時完成一定的開拓、采準、剝離的工程量。露天礦在開采過程中，必須將境界內的礦、巖劃分成一定厚度的水平分層，以便由上向下逐層進行開采，這些階梯塊的工作面叫做臺階。每個臺階大多使用獨立的穿孔和采掘設備。由于露天開采在采出礦石的同時，必須剝離一定數量的巖石。而且，剝離巖石量的多少直接影響采出礦石的成本和單位投資額，并且隨著礦山開采深度變化往往剝離巖石的數量也是變化的。而這些礦石與巖石的搬卸運輸就成了露天礦場經濟利益中最為重要的一環。本文將利用優化模型中整數優化的思想[1]針對這一問題展開詳細討論。

1 礦車運輸組織模型的模型分析

礦車運輸組織本質上屬于貨運車輛運行調度問題，而此問題正式貨運企業運輸生產管理活動中一個非常重要的組成部分。車輛運行調度工作是以車輛的運行為中心，不但是高質量完成預定的貨運任務的保證，而且通過車輛運行作業計劃的實施也將企業內部各生產環節（特別是車隊、車間裝卸部門等）連接成一個有機的整體[2]。交通運輸組織是通過交通規劃的手段有計劃的引導交通的一系列運動，即規劃者如何提示各種目標。事實上，運輸組織可以理解為有限的道路空間上綜合運用交通規劃、交通限制和管理等手段，科學有效的地分時、分路、分車種、分流向使用道路，使交通狀況始終處于有序、高效運行狀態。其用意在于分解車流矛盾。一般好的交通組織主要考慮在時間上削峰填谷，避免空間上過于稀疏或者過于擁擠，體現出矛盾分散、時空均分的原則。一般對于道路通行時空資源的分配優化，重點是要解決通行能力、路權分配問題以及路網負荷均分問題。

貨車運行調度工作主要內容包括：檢查貨運生產前的作業準備情況；檢查車輛運行作業計劃的執行情況；根據車輛的技術狀況和所處狀態，科學合理的調配車輛，提高車輛運用水平；根據主要物資的流量、流向及其變化規律，加強回程貨源的組織工作，提高車輛運行水平；根據營運區域內的道路和交通情況，及時調整車輛的運行線路；合理調配勞動力，加強勞動組織工作；運用現代信息技術，對車輛和貨物進行跟蹤和實時控制。

對于礦車運輸調度優化問題來說一般主要考慮兩方面的因素。首先，它要求單位路程總運量最大；其次，要求動用的載貨車量數最少。可見礦車運輸調度計劃編制這類問題的難點在于，如果礦車數量過少，那么礦產的運輸效率將大幅度降低；相反，如果礦車數量太多，又會出現礦車現在浪費投資的現象。不難看出，礦車運輸調度優化問題實際上可以看作是一個多目標優化問題[3-5]。從數學的角度來說，由于多目標規劃其各個子目標之間往往是相互矛盾的（例如：我們既想礦車數量少，又想總運量最大），因此通常來說多目標問題的最大的特點就是不易獲取其全局最優解。除此之外，礦產車輛的運輸調度過程中往往還存在著，待優化變量規模大（即，礦產車輛的數量大、種類多）不易高效求解的問題。在現實中為了解決這類問題，人們往往采取貪心準則的優化策略，這樣做的好處是，貪心準則的算法復雜度低，便于在實際中實現。但是貪心算法只能獲得局部最優解而非全局最優解，這就會對實際生產中礦車運輸調度的效率帶來嚴重的影響。為了從本質上解決目前礦車運輸調度存在的問題，本文提出了一種基于多目標規劃思想的礦車運輸調度優化模型。

在建立模型前，我們首先需要做幾個模型基本的假設：1）假設卡車在鏟點和卸點不存在等待排隊現象；2）各個裝卸點均達到規定產量；3）不考慮卡車存在偶然的交通事故。在這3條假設的基礎上，我們將在下一節中介紹本文所提出的數學模型。

2 礦車運輸調度優化模型的建立

在上一節中我們提到，礦車的運輸組織及運行調度主要考慮2個因素，即單位路程總運量和運輸作業中動用的載貨車輛數。也就是說，該優化問題至少存在兩個優化目標，且兩個決策要求各有其合理性；同時在做最終決策時，無需強調絕對意義上的最優性，因而我們需構造一種更適用于實際決策過程的優化模型。此外，我們優化模型參與的參量主要包括礦車數量，礦產量以及單位單位路程上的礦石運輸量。

下面首先針對第一個優化目標——單位路程總運量最大，建立數學模型，見式（1）。

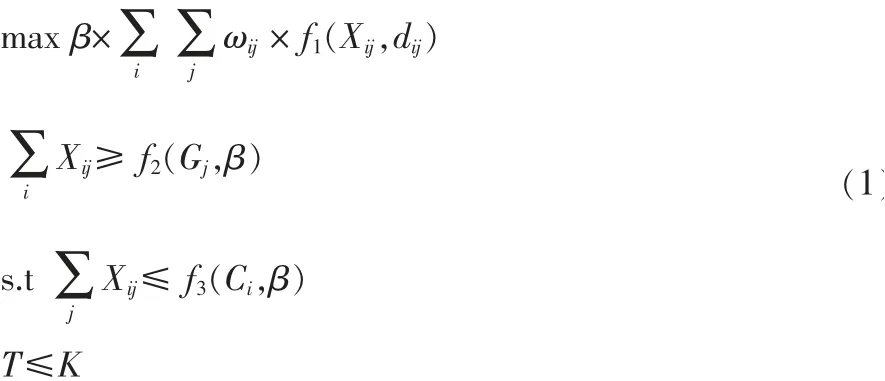
其中，f1（Xij，dij）=Xij/dij；f2（Gj，β）=Gj/β；f3（C，β）=Ci/β；β是卡車的運載量；Xij是第i個鏟點到第j個卸點的運載次數；dij是第i個鏟點到第j個卸點的距離；ωij是加權系數；Gj是第j個卸點的產量；Ci是第i個鏟點的產量；T為動用卡車的數量；K卡車數量的上限。

這里有必要對上述模型做簡要的說明。首先式（1）所給出的優化模型中，其代價函數所描述的是要求所有卡車的總的運輸量最小，也就單位路程總運量最大。因為在需要運送礦石的總量不變的情況下，距離越近則意味著總運量就越小。換句話說，本優化目標的含義是要求所有載貨車輛以最短的路徑進行貨物運輸工作。此外，對于模型中約束條件簡要解釋，第一個約束條件是要求第個卸點的總產量必須大于或等于此卸點產量的約束；第2個約束條件是要求第個鏟點運送的礦石量小于該鏟點的產量；最后一個約束條件是要求卡車的數量不能超過所能采用的卡車數量極限。由此可以看出，優化模型所給出的3個約束條件能夠使得本優化模型更加符合實際生產情況和相應要求。

針對目標二——動用的載貨車輛數最少，建立的數學模型如下。

在模型（2）中所有的約束條件與模型（1）一致，即，是要保證在讓載貨車輛數最少的同時還能同時使得車輛數滿足基本的貨物運輸要求。從數學角度上說，就是使得優化得出的車輛數不會出現“奇異值”（例如：負值），因為很顯然如果沒有合理的約束條件式（2）所示的優化模型的全局最優解應該為負無窮。上一節中我們提到，根據現有的運籌學技術條件，聯立求解式（1）與式（2）所示的多目標優化模型并不容易，一般來說解決多目標規劃一種常規思想就是將多目標轉化成為單目標，這個思想下最常見的做法就是將多個目標進行線性組合，使得組合后的目標極大或者極小。本文采用一種較為新穎的基于“極大極小”的優化思想的轉化策略將這個雙目標問題轉化成為一個單目標問題后再進行求解[6]，轉化后模型如下所示。點法，梯度下降法和空間投影法等一些優化領域里的成熟的算法進行求解[7]。值得一提的是，由于式（3）所示的模型其求解簡單，所以式（3）所示的優化模型還可以根據實際需要在約束條件中繼續增加更多實際中所需要的約束條件，例如：運輸時間，運輸費用的限制等等。因此，我們說本文模型另一個優勢是具有良好的推廣性。

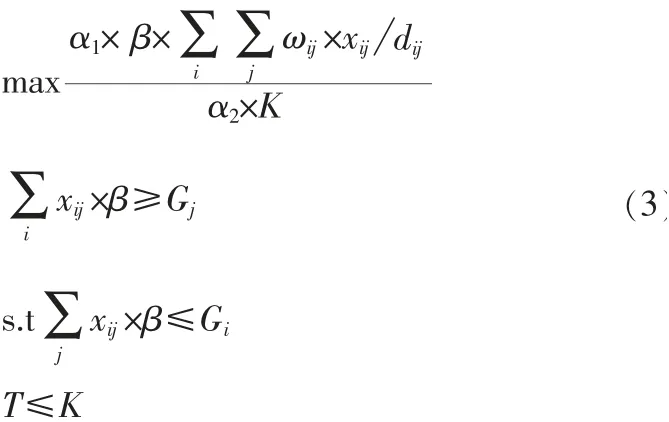
3 模型結果分析

從式（3）不難看出，此時通過合理轉化，我們已經將原有的多目標優化問題簡化成為了一個單目標優化問題，使得式（3）最小的條件此時顯然是使得式（1）與式（2）一起最小的必要條件。雖然，式（3）所示的優化模型是一個非線性規劃模型，但是由于分子和分母都是線性函數，因此可以方便的使用內

為了驗證上一節給出的礦車運輸調度優化模型的可行性，在本節中我們將采用某礦場的實際數據進行算法模擬。這里將分別采用本文提出的方法和傳統的貪心算法進行比較，采用對比分析法驗證本算法的優越性。

某礦場的實際生產數據如表1所示。

表1 礦場數據分布Tab.1 Mine data distribution

通過將表1所示的礦場分布數據帶入上一節給出的礦車運輸調度優化模型，計算得出的單位運量24.89萬噸，而同時執行該計劃所需礦車僅為25量。相應的，傳統貪心算法得到的單位運量僅為21.543萬噸，所需礦車為29量。從實驗結果對比很容易看出，本文提出的基于多目標優化的方法相較于傳統的優化方法有明顯的優勢。

4 結 論

交通組織是指通過交通規劃的手段有計劃的引導交通的一系列運動，使得機動化程度的增長從而節約了運輸時間、降低了運費、降低了產品的成本、促進了物資的流通。礦車交通組織的合理優化是提高礦區生產效率的核心問題，是能夠提高礦區經濟效益的有效途徑。本文利用運籌學中多目標優化的思想提出了一種礦車運輸調度優化模型，并且通過極大極小的方法將雙目標問題轉化為一個單目標問題，簡化了求解過程。通過對比分析可以看出，本文所設計的算法遠遠優于傳統的貪心算法，因此適于應用到實際的礦車生產調度工作中，體現其重要的實踐指導意義。

[1]《運籌學》教材編寫組.運籌學[M].北京：清華大學出版社，2005.

[2]戴彤焱，孫學琴.運輸組織學[M].北京：機械工業出版社，2011.

[3]吳祈宗.運籌學與最優化方法[M].北京：機械工業出版社，2008.

[4]胡斌，王國平，李國強.采用多目標改進差分進化算法的環境經濟發電調度[J].陜西電力，2013（1）：24－27.HU Bin，WANG Guo-ping，LI Guo-qiang.Probe into environmental economic dispatching adopting multiobjective improved differential evolution algorithm[J].Shaanxi Electric Power，2013（1）：24－27.

[5]寧姍.基于蟻群聚類的多目標環形分類的方法研究[J].工業儀表與自動化裝置，2012（5）：70－73.NING Shan.Research on annular sort of multi-objects based on ant colony clustering[J].Industrial Instrumentation&Automation，2012（5）：70－73.

[6]姜啟源，謝金星，葉俊.數學模型[M].北京：高等教育出版社，2010.

[7]陳寶林.最優化理論與方法[M].北京：清華大學出版社，2005.

[8]Giordano，F.R.等著.葉其孝等譯.數學建模[M].3版.北京：機械工業出版社，2005.