一種新型壓氣機葉片造型方法的平面葉柵試驗驗證

安利平，李清華，劉劍鵬，馬昌友

一種新型壓氣機葉片造型方法的平面葉柵試驗驗證

安利平，李清華，劉劍鵬，馬昌友

(中國燃氣渦輪研究院，四川成都610500)

為驗證一種新型超/跨聲壓氣機葉片造型方法——B樣條控制中線角葉型、貝塞爾曲線控制葉型厚度方法(BMAA方法)的有效性，分別與原有的可控擴散葉型定制造型和任意中線造型進行平面葉柵對比試驗。結果表明，BMAA方法得到的跨聲葉型，具有比定制葉型更優(yōu)的氣動性能；BMAA方法得到的超聲葉型，具有與任意中線葉型相似的氣動性能；與傳統(tǒng)葉片造型方法相比，BMAA方法具有更高的效率，可提高葉片的氣動負荷。

超/跨聲壓氣機；高負荷葉型；葉片造型方法；B樣條控制中線角葉型；任意中線葉型；定制葉型；平面葉柵試驗

1 引言

現(xiàn)代航空發(fā)動機對壓氣機的性能要求越來越高，不但要有很高的壓比，還要有較高的效率和一定的穩(wěn)定工作裕度。隨著壓氣機級負荷的提高，其輪緣速度也越來越高，引起葉片排內(nèi)的超/跨聲速流動。研究和應用表明，這類壓氣機是高效、高負荷壓氣機發(fā)展的方向，而超/跨聲葉片造型技術是該類壓氣機設計的關鍵技術。

在目前常用的定制葉型造型技術[1](CDA方法)和任意中線造型技術[2，3](AMA方法)基礎上，安利平等[4]開發(fā)了采用B樣條曲線控制中線、貝塞爾曲線控制葉型厚度的一種新的葉片造型方法(BMAA方法)。數(shù)值模擬分析表明，該造型方法可適用于超、跨聲范圍的葉型設計，具有無量綱控制參數(shù)較少、彎度控制靈活、葉型型面光滑、計算性能良好等優(yōu)勢。

為進一步驗證該造型方法的有效性，本文針對跨聲葉型和超聲葉型，分別選取相同的設計參數(shù)，采用BMAA方法和其它造型方法進行平面葉柵設計和對比試驗。對于跨聲葉型，選取BMAA葉型與定制葉型進行對比試驗；對于超聲葉型，選取BMAA葉型與任意中線葉型進行對比試驗。

2 試驗設置及方法

2.1試驗設備

平面葉柵試驗在中國燃氣渦輪研究院暫沖大氣吹入式超、跨聲速平面葉柵風洞[5]上進行。試驗器由氣源站供給高壓空氣，空氣經(jīng)凈化、干燥后貯存于貯氣罐中。風洞與高壓貯氣罐相接，最大質量流量為22.4 kg/s，穩(wěn)定工作時間大于4 min，壓力波動不大于0.3%。快速閥為電動控制閥，從關閉至全開只需3 s。試驗段工作圓盤可在20°～90°范圍內(nèi)轉動，以滿足不同進口氣流角的試驗要求。

2.2試驗葉型

為驗證BMAA葉型造型方法的有效性，利用BMAA和CDA方法，在相同進出口氣流角、攻角、落后角等條件下，設計兩套平面葉柵進行跨聲葉柵對比試驗；利用BMAA和AMA方法，在相同進出口氣流角、攻角、落后角等條件下，設計兩套平面葉柵開展超聲葉柵對比試驗。葉型詳細參數(shù)如表1所示，文中角度按葉柵額線方向定義。

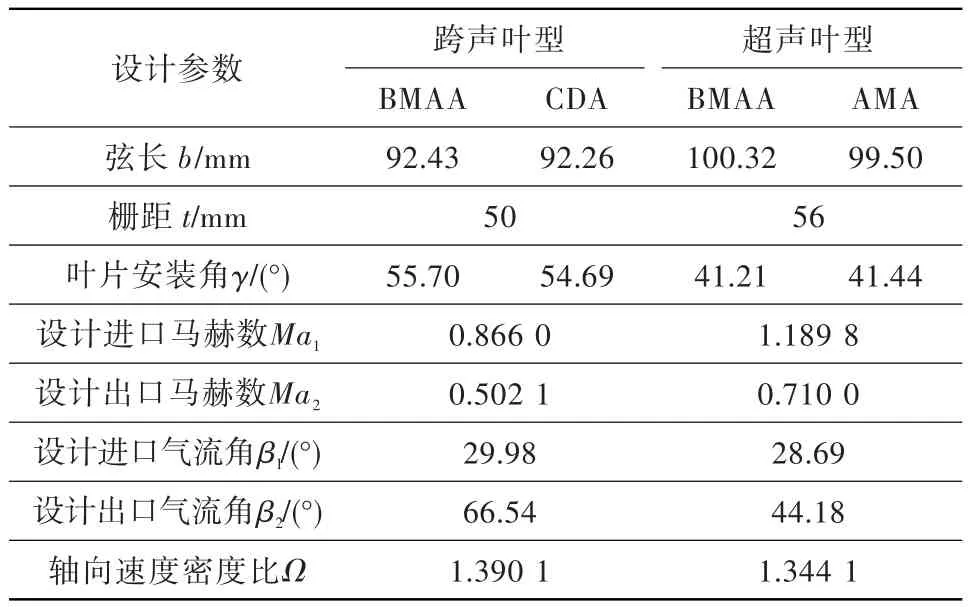
表1 葉型幾何和氣動設計參數(shù)Table 1 Airfoil geometric and aerodynamic design parameters

3 BMAA造型與CDA造型試驗結果對比

3.1葉型表面馬赫數(shù)分布

高性能葉柵設計從控制葉柵葉型表面馬赫數(shù)分布出發(fā)，通過馬赫數(shù)分布，可分析氣流在葉片表面的加速、減速、流動分離及激波位置等現(xiàn)象。

圖1分別為BMAA和CDA造型葉柵，在Ma1= 0.866、進口氣流攻角i=-4°～4°范圍時葉片表面的馬赫數(shù)分布。可見，BMAA葉型表面流動狀態(tài)良好，只在近堵點i=-4°時，葉背出現(xiàn)槽道激波；CDA葉型在i＞2°時表面流動狀態(tài)良好，當i＜2°時葉背表面馬赫數(shù)出現(xiàn)兩個峰值，說明通道內(nèi)出現(xiàn)了兩道激波。

圖2分別為BMAA和CDA造型葉柵在β1下，進口馬赫數(shù)Ma=0.6～1.0范圍內(nèi)時，葉片表面的馬赫數(shù)分布。由圖中可知：對于BMAA造型葉柵，隨著Ma的增加，葉柵表面馬赫數(shù)增加；當Ma≥0.866 0時，葉背出現(xiàn)超聲區(qū)，隨著進口馬赫數(shù)的繼續(xù)增加，葉背峰值馬赫數(shù)增加，槽道超聲流動為單波結構。對于CDA造型葉柵，Ma≥0.866 0時葉背出現(xiàn)超聲區(qū)，且槽道內(nèi)形成兩道激波，葉柵損失增大。

3.2葉型損失

葉柵損失系數(shù)ω表征氣流流經(jīng)葉柵通道后，總壓損失占進口氣流動壓頭的比例。

圖3給出了BMAA和CDA造型葉柵在Ma1下，葉柵損失系數(shù)隨進口氣流角β的變化。圖4則給出了BMAA和CDA造型葉柵在β1下，葉柵損失系數(shù)隨Ma的變化趨勢對比。

由圖3可知，在Ma1下、i=-4°～4°時，BMAA造型葉柵氣流損失明顯小于CDA造型葉柵，非設計攻角下葉型損失差異增加。由圖4可知，在β1下、Ma= 0.6～1.0時，BMAA造型葉柵氣流損失略小于CDA造型葉柵，且隨著Ma的增加，葉型損失差異增加。

3.3葉柵壓比

壓氣機葉柵壓比π＞1時，π越大，說明壓氣機對氣流的增壓作用越大；π＜1時，表明壓氣機葉柵進入渦輪工作狀態(tài)。

圖1不同進氣攻角下跨聲葉柵表面的馬赫數(shù)分布Fig.1 The distribution of cascade surface Mach number at different inlet flow angle

圖5 示出了BMAA和CDA造型葉柵在Ma1下，π隨β的變化趨勢。圖6示出了BMAA和CDA造型葉柵在β1下，π隨Ma的變化趨勢。

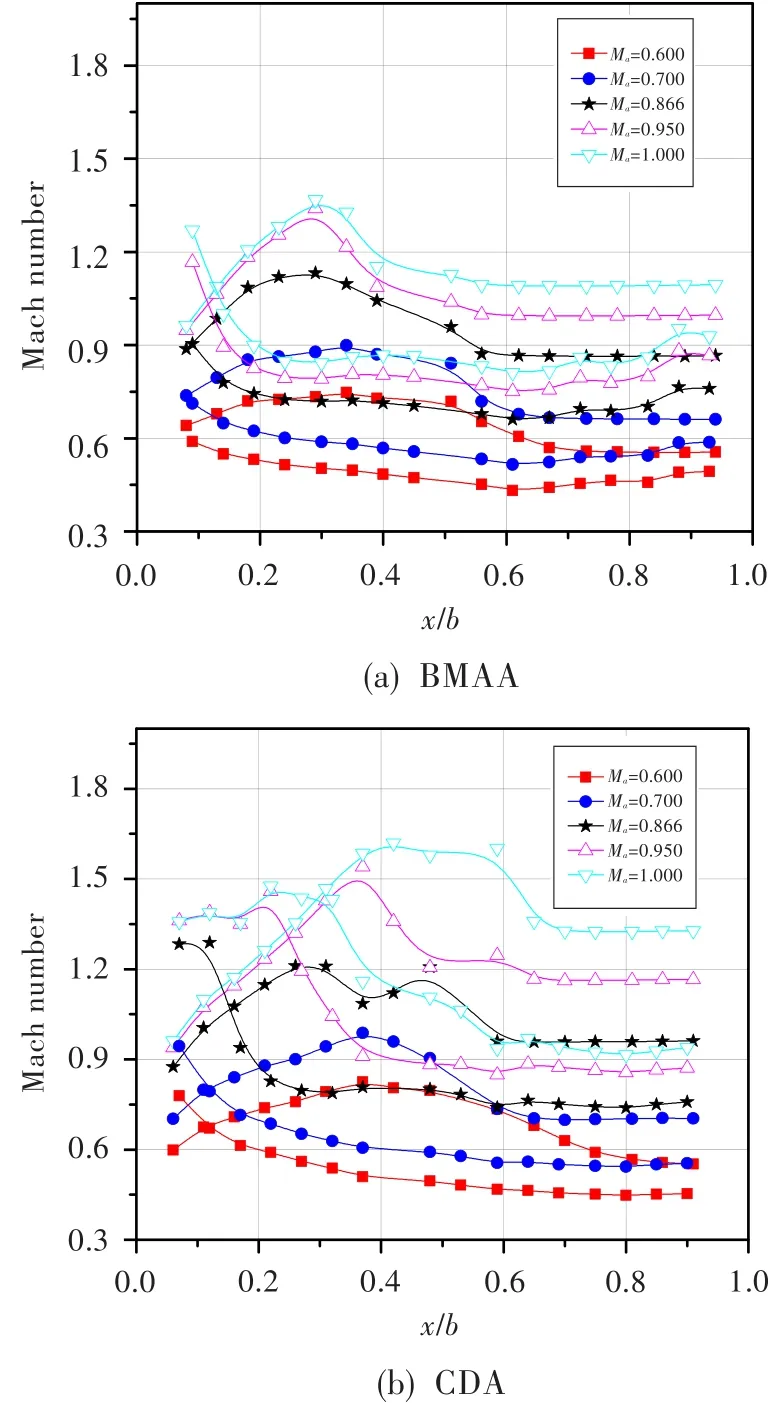
圖2 不同進口馬赫數(shù)下跨聲葉柵表面的馬赫數(shù)分布Fig.2 The distribution of transonic cascade surface Mach number at different inlet flow Mach numbers

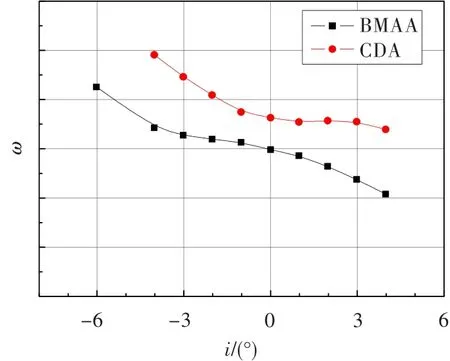
圖3 跨聲葉型損失隨進氣攻角的變化Fig.3 The transonic cascade loss loop for different inlet flow angle

由圖中可知，在Ma1下、不同i時，BMAA葉柵壓比均大于CDA葉柵，且其進入渦輪工作狀態(tài)的攻角小于CDA葉柵；在β1下，不同Ma時BMAA葉柵壓比略大于CDA葉柵，尤其是在Ma=0.80～0.92范圍內(nèi)，兩葉型的壓比差異較明顯。

根據(jù)以上對比分析可看出，在Ma=0.6～1.0、i=-4°～4°范圍內(nèi)，BMAA葉型在葉柵表面流動、葉型損失和葉柵壓比等方面均優(yōu)于CDA葉型。

圖4 跨聲葉型損失隨進口馬赫數(shù)的變化趨勢Fig.4 The transonic cascade loss loop for different inlet flow Mach numbers

圖5 跨聲葉型壓比隨進氣攻角的變化趨勢Fig.5 The transonic cascade pressure ratio at different inlet flow angle

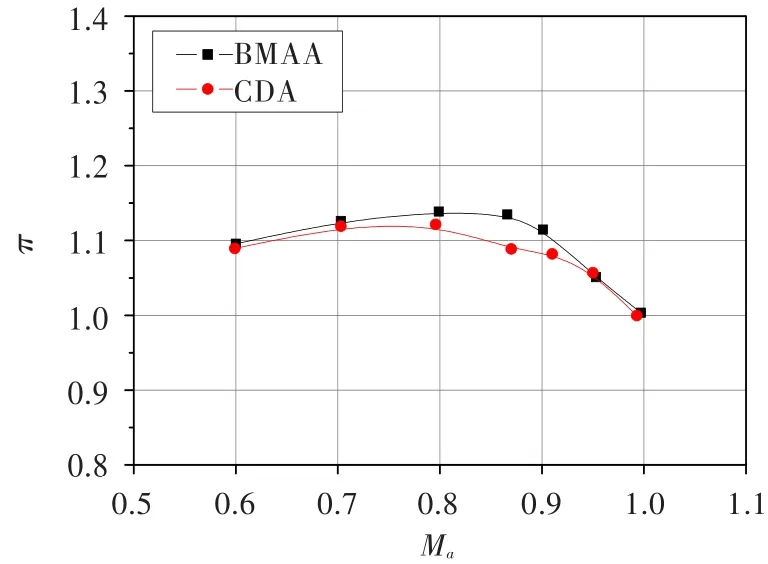
圖6 跨聲葉型壓比隨進口馬赫數(shù)的變化趨勢Fig.6 The transonic cascade pressure ratio at different inlet flow Mach numbers

4 BMAA造型與AMA造型試驗結果對比

主要對比β1下不同Ma時葉柵流道和性能差異。

4.1葉型表面馬赫數(shù)分布

圖7分別給出BMAA和AMA造型葉柵，在β1下、Ma＝0.90～1.25時，葉片表面的馬赫數(shù)分布。可見，兩葉柵在Ma=0.90狀態(tài)下，葉背前緣附近(≤20%弦長)表面馬赫數(shù)迅速增大，之后變化較小，在60%弦長附近達到峰值，而后氣流減速增壓；葉盆表面馬赫數(shù)平穩(wěn)、較小，葉片表面馬赫數(shù)分布趨勢平緩。Ma≥1.0時，兩葉柵表面馬赫數(shù)分布近似，葉背都出現(xiàn)雙波結構，且隨著Ma的增大迅速增大，葉背表面馬赫數(shù)峰值向后移動；葉盆表面馬赫數(shù)分布在葉盆前緣附近開始出現(xiàn)加速區(qū)，且隨著Ma的增大加速區(qū)逐漸擴大；BMAA葉型50%弦長之前，葉盆、葉背表面馬赫數(shù)略低于任意中線葉型，第二個葉背表面馬赫峰值則略高于任意中線葉型。

4.2葉型損失與壓比

圖8和圖9分別給出了兩套葉柵在β1下，葉柵損失系數(shù)和葉柵壓比隨Ma的變化。由圖8可知，在不同Ma下，兩葉型的損失基本相當，多數(shù)情況下BMAA葉型損失略低，在Ma＝1.1左右，AMA葉型損失略低。

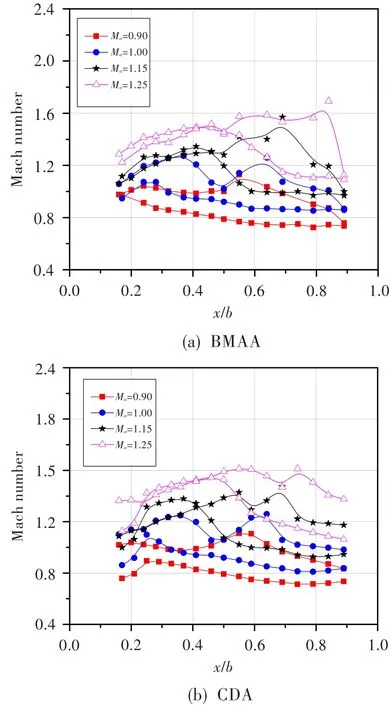
圖7 不同進口馬赫數(shù)下超聲葉型表面的馬赫數(shù)分布Fig.7 The distribution of supersonic cascade surface Mach numbers at different inlet flow Mach numbers

由圖9可知，當Ma＜1.1時，BMAA葉型壓比低于AMA葉型；當Ma≥1.1時，兩葉柵的壓比基本相當；在Ma=1.189 8的設計點時，BMAA葉型壓比略高于AMA葉型。

據(jù)此可認為，在超、跨聲進口條件下，BMAA葉型與AMA葉型性能基本相當。

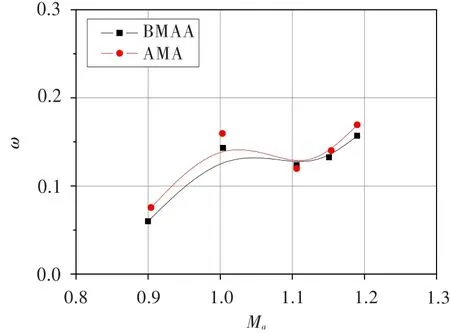
圖8 超聲葉型損失隨進口馬赫數(shù)的變化趨勢Fig.8 The supersonic cascade loss loop for different inlet flow Mach numbers

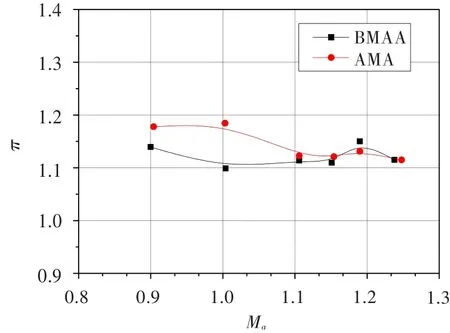
圖9 超聲葉柵壓比隨進口馬赫數(shù)的變化Fig.9 The supersonic cascade pressure ratio at different inlet flow Mach numbers

5 結論

通過平面葉柵試驗，對文獻[4]提出的一種基于計算幾何控制無量綱參數(shù)葉片造型方法的有效性予以了驗證。結果表明，在亞聲和跨聲進口條件下，BMAA葉型性能優(yōu)于定制葉型；在跨/超聲進口條件下，BMAA葉型性能與任意中線葉型相當。當前，已完成了對BMAA葉片造型方法的軟件開發(fā)、數(shù)值模擬和葉柵試驗驗證等研究工作，證明本造型方法可用于超/跨聲葉型工程設計，是提高風扇/壓氣機負荷、效率的先進設計技術。

[1]程榮輝，周拜豪，余華蔚，等.定制葉型技術及其在壓氣機設計中的應用[J].燃氣渦輪試驗與研究，2000，13(1)：15—22.

[2]Crouse J E，Janetzke D C，Schwirian R E.A Computer Pro?gram for Composing Compressor Blading from Simulated Circular-Arc Elements on Conical Surfaces[R].NASA TN K-5437，1969.

[3]冀國鋒，桂幸民.軸流/離心壓氣機葉片通用任意中弧線設計方法[J].航空動力學報，2009，24(1)：150—156.

[4]安利平，黃萍.一種基于計算幾何控制無量綱參數(shù)的葉片造型方法[J].燃氣渦輪試驗與研究，2013，26(4)：8—12.

[5]向宏輝，任銘林，馬宏偉，等.兩類葉型探針對擴壓葉柵流場影響的對比[J].燃氣渦輪試驗與研究，2011，24(3)：26—30.

Verification of an Innovative Blading Method by Planar Cascade Test

AN Li-ping，LI Qing-hua，LIU Jian-peng，MA Chang-you
(China Gas Turbine Establishment，Chengdu 610500，China)

The advantage and feasibility of a newly developed blade modeling method(BMAA)was validat?ed by a planar cascade test compared with the former CDA method and the arbitrary camber lines method. The test results show that the transonic blade generated by the new method achieved better aerodynamic performance than CDA method;and the performance of supersonic blade is equal to that of arbitrary camber lines;the blade generated by the new method have higher efficiency and blade aerodynamic load which are superior to the conventional blade.

super/trans-sonic compressor；high loading airfoil；blading method；BMAA method；arbitrary camber lines method；tailored airfoil method；planar cascade test

V232.4

A

1672-2620(2013)05-0012-04

2013-07-08；

2013-09-24

安利平(1977-)，男，陜西富平人，高級工程師，碩士，主要從事壓氣機設計工作。