基于雙相介質(zhì)的地震流體識(shí)別

印興耀,李 超,張世鑫

(1.中國(guó)石油大學(xué)地球科學(xué)與技術(shù)學(xué)院,山東青島 266580;2.中海油研究總院,北京 100027）

基于雙相介質(zhì)的地震流體識(shí)別

印興耀1,李 超1,張世鑫2

(1.中國(guó)石油大學(xué)地球科學(xué)與技術(shù)學(xué)院,山東青島 266580;2.中海油研究總院,北京 100027）

為避免間接計(jì)算的累積誤差,提高儲(chǔ)層流體識(shí)別精度,根據(jù)孔隙彈性介質(zhì)理論,建立基于彈性阻抗反演的流體因子直接提取方法和固液解耦流體因子疊前地震反演方法。地震波在含烴儲(chǔ)層中傳播時(shí)發(fā)生速度頻散,根據(jù)中觀尺度巖石物理理論,提出基于疊前反演的頻散屬性提取方法,實(shí)現(xiàn)頻散屬性的定量表征,將速度的頻散幅度用于流體識(shí)別。該方法實(shí)際工區(qū)應(yīng)用效果良好。結(jié)果表明：以雙相介質(zhì)巖石物理理論為基礎(chǔ)建立流體因子,依托疊前地震反演進(jìn)行儲(chǔ)層流體識(shí)別的方法精確可靠。

雙相介質(zhì);流體識(shí)別;彈性阻抗;疊前地震反演;頻散屬性

基于地震資料的儲(chǔ)層流體識(shí)別是一項(xiàng)在巖石物理理論指導(dǎo)下將與孔隙流體有關(guān)的異常特性表征為流體因子,利用流體因子實(shí)現(xiàn)介質(zhì)孔隙流體的類型判別的技術(shù)。20世紀(jì)七八十年代,利用“亮點(diǎn)”現(xiàn)象進(jìn)行儲(chǔ)層預(yù)測(cè)的技術(shù)得到廣泛應(yīng)用[1-2]。1987年, Smith等[3]率先提出利用縱橫波速度相對(duì)變化量的加權(quán)疊加判別儲(chǔ)層含烴異常,并給出了流體因子的概念。Goodway等[4]提出了LMR技術(shù),使用拉梅常數(shù)和密度進(jìn)行流體指示的方法。Gassmann[5]在一定的假設(shè)前提下,推導(dǎo)了表征雙相介質(zhì)彈性模量參數(shù)的Gassmann方程。Russell等[6-7]指出Gassmann流體項(xiàng)f可以直接作為一項(xiàng)流體因子參與流體檢測(cè)。印興耀等[8]提出了包含Gassmann流體項(xiàng)的彈性阻抗方程,可以直接反演高精度的流體項(xiàng)。考慮到地震波經(jīng)過(guò)油氣儲(chǔ)集層后表現(xiàn)出吸收衰減、速度頻散等異常現(xiàn)象,可以利用地震資料中所蘊(yùn)含的頻率信息進(jìn)行儲(chǔ)層描述與流體識(shí)別。2009年,Wilson等[9]基于Chapman巖石物理模型[10]將Smith& Gidlow兩項(xiàng)AVO反射系數(shù)近似公式看作與頻率的函數(shù),給出了頻散屬性表達(dá)式。吳小羊等[11]利用基于偽平滑Wigner-Ville分布的頻譜分析技術(shù)和AVO反演結(jié)合進(jìn)行頻散屬性的AVO反演。筆者首先在雙相介質(zhì)巖石物理理論的基礎(chǔ)上,研究基于彈性阻抗反演的流體因子直接提取方法以及等效流體體積模量的直接反演方法,進(jìn)一步消除多孔介質(zhì)固體孔隙效應(yīng)的影響,最后推導(dǎo)包含頻散屬性的反射系數(shù)近似公式,建立反演矩陣方程及相應(yīng)的反演方法,進(jìn)行高精度的儲(chǔ)層流體識(shí)別。

1 基于振幅信息的流體因子

流體因子(fluid factor）的構(gòu)建是儲(chǔ)層流體識(shí)別的關(guān)鍵。流體因子最早由Smith等提出,特指由縱橫波速度相對(duì)變化量權(quán)差運(yùn)算構(gòu)成的一種參數(shù)。隨著研究深入,流體因子這一概念已不單指某種特定的參數(shù),可給予其更為寬泛的含義,即對(duì)某研究工區(qū)而言,能夠?qū)?chǔ)層孔隙流體類型進(jìn)行有效區(qū)分的參數(shù)都可以稱為“流體因子”,而對(duì)于不同工區(qū),流體因子各異,需通過(guò)流體因子敏感性分析進(jìn)行統(tǒng)計(jì)分析。

1.1 Gassmann流體項(xiàng)

相比常規(guī)的基于單相介質(zhì)理論的流體因子(如泊松比σ,拉梅參數(shù)λ以及λρ等）來(lái)說(shuō),基于雙相介質(zhì)理論得到的Gassmann流體項(xiàng)f能夠更好地表征孔隙流體對(duì)巖石介質(zhì)的彈性影響,其主要體現(xiàn)在基于雙相介質(zhì)理論的流體因子受巖石固體骨架等因素的影響要遠(yuǎn)小于基于單相介質(zhì)提出的流體因子。

假設(shè)固體骨架礦物相同,孔隙中包含水和氣,采用流體替代方式計(jì)算兩者隨含水飽和度和孔隙度的變化趨勢(shì),結(jié)果如圖1(巖石孔隙飽含水和氣）所示。通過(guò)比較拉梅參數(shù)λρ與Gassmann流體項(xiàng)f隨孔隙度和含水飽和度變化的趨勢(shì),可以看到孔隙度對(duì)λρ的影響遠(yuǎn)大于孔隙流體類型對(duì)其產(chǎn)生的影響,而飽含相同孔隙流體類型的f數(shù)值雖然也隨孔隙度產(chǎn)生一定的畸變,但是對(duì)流體類型的表征已經(jīng)遠(yuǎn)優(yōu)于λρ。進(jìn)一步地,還可比較μρ、Ip、λρ、f、σ、I2p-cI2s和λμ等流體因子的流體指示系數(shù),圖2為某研究區(qū)實(shí)際測(cè)井資料統(tǒng)計(jì)得到的流體指示系數(shù)統(tǒng)計(jì)直方圖。通過(guò)比較可知,Gassmann流體項(xiàng)f對(duì)該工區(qū)的流體指示較為敏感,說(shuō)明在該工區(qū)利用f進(jìn)行儲(chǔ)層流體識(shí)別有較大優(yōu)勢(shì)。

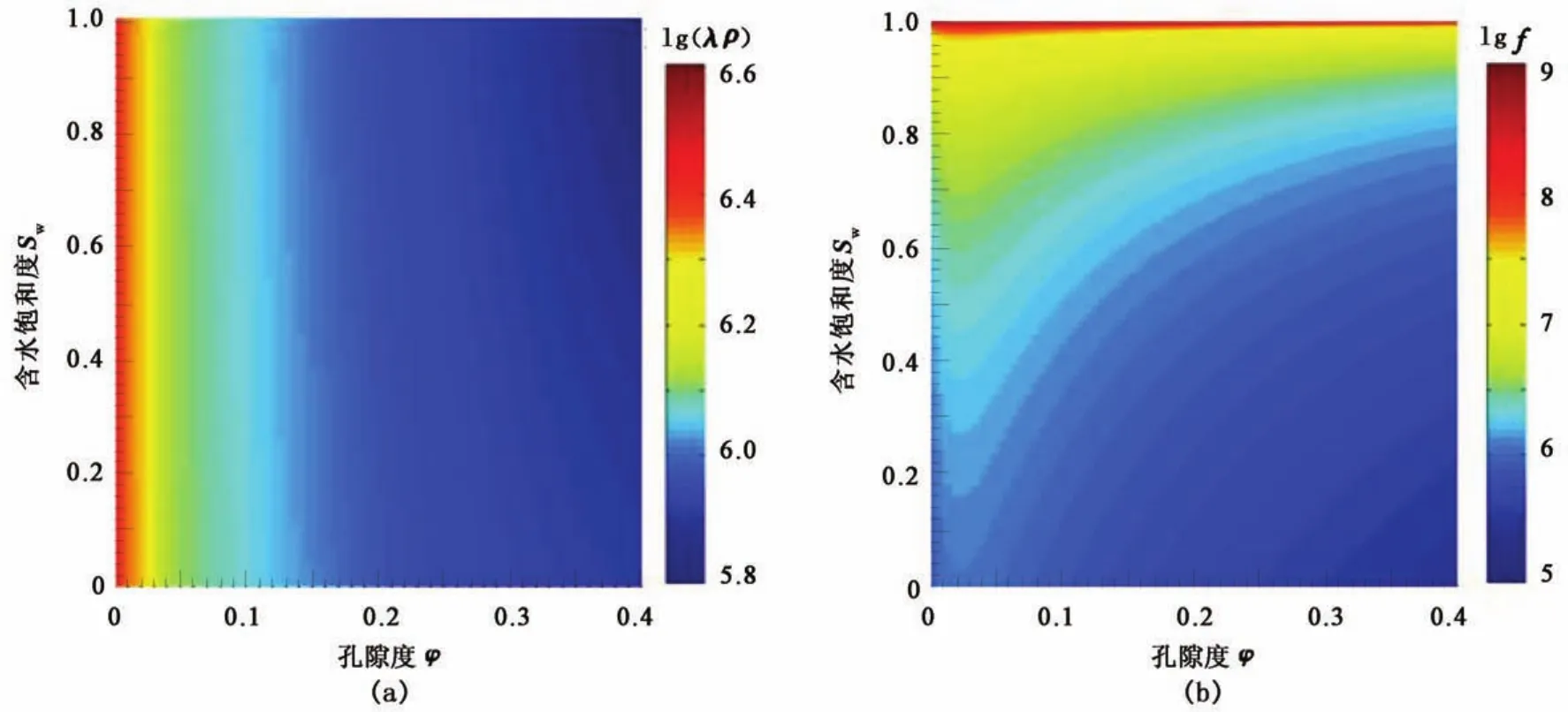
圖1 流體因子隨孔隙度與含水飽和度的變化趨勢(shì)Fig.1 Variation of fluid factor with porosity and water saturation

圖2 流體指示系數(shù)比較圖Fig.2 Comparison of fluid factor indication factors

在流體因子疊前地震反演中一般考慮直接反演敏感流體因子,一方面可避免間接計(jì)算帶來(lái)的累積誤差[12];另一方面,在某些情況下,還可以避免無(wú)法反演密度參數(shù)帶來(lái)的誤差。

利用彈性阻抗反演方法,流體彈性阻抗方程可以表示為

由方程(2）可知,當(dāng)入射角θ=0時(shí),標(biāo)準(zhǔn)化的彈性阻抗取值為聲阻抗vPρ,當(dāng)入射角非零時(shí),標(biāo)準(zhǔn)化的彈性阻抗數(shù)值也在聲阻抗vPρ附近波動(dòng),從而將EI(θ）數(shù)值統(tǒng)一到阻抗量綱,且保證了后續(xù)參數(shù)提取的穩(wěn)定性。利用大、中、小三個(gè)角度的部分角度疊加道集分別進(jìn)行彈性阻抗反演,反演得到流體彈性阻抗后聯(lián)立三個(gè)角度的阻抗方程即可得到流體因子f。

將上述方法應(yīng)用于勝利油田某工區(qū)進(jìn)行含烴異常檢測(cè),圖3是反演得到的Gassmann流體項(xiàng)的過(guò)井剖面圖。結(jié)合測(cè)井和鉆井的解釋結(jié)果,圖中的儲(chǔ)層預(yù)測(cè)結(jié)果與鉆遇結(jié)果較吻合,驗(yàn)證了該方法在儲(chǔ)層流體識(shí)別方面的可靠性。

圖3 Gassmann流體項(xiàng)反演剖面Fig.3 Inverted Gassmann fluid factor

1.2 流體體積模量

Gassmann流體項(xiàng)本身存在固液兩相耦合的問(wèn)題,由圖1(b）可知,實(shí)際上f除受孔隙流體影響之外,還受到巖石骨架固有的固體效應(yīng)(巖石基質(zhì)、孔隙度等）的綜合影響,f隨含水飽和度變化趨勢(shì)受孔隙度影響有一定的畸變,因此在某些工區(qū)的實(shí)際應(yīng)用中還需要注意儲(chǔ)層巖石的固體效應(yīng)(特別是孔隙度）造成的流體識(shí)別假象。

圖4所示為不同孔隙度與含水飽和度情況下的Kf變化趨勢(shì)。從圖中可以看出,Kf與含水飽和度呈完全線性變化趨勢(shì),且完全不受孔隙度的影響。因此,如果采用特定的地球物理方法從地震資料中提取出流體體積模量參數(shù)Kf,將其作為一項(xiàng)流體因子參與流體識(shí)別,即可實(shí)現(xiàn)固體骨架與流體彈性效應(yīng)的解耦,從而有效地提高了儲(chǔ)層孔隙流體識(shí)別的可靠性[13]。

Han和Batzle等[14-15]通過(guò)對(duì)碎屑巖進(jìn)行巖石物理統(tǒng)計(jì),研究了Biot-Gassmann理論中的孔隙流體與巖石骨架的固體效應(yīng)(孔隙度,礦物模量等）對(duì)巖石模量信息的耦合作用,提出了突出流體等效體積模量Kf的Gassmann流體項(xiàng)的經(jīng)驗(yàn)公式：示巖石骨架礦物與孔隙度的綜合作用。

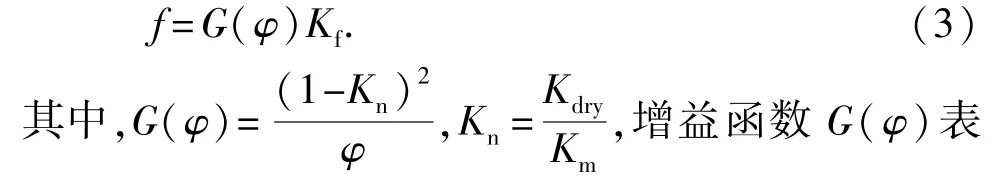
圖4 流體體積模量隨孔隙度與含水飽和度的變化趨勢(shì)Fig.4 Variation of fluid bulk modulus with porosity and water saturation

Nur[16]通過(guò)大量研究指出,對(duì)于小于臨界孔隙度的巖石來(lái)說(shuō),其干巖石的體積模量和剪切模量可以用與臨界孔隙度φc有關(guān)的線性函數(shù)表示,即臨界孔隙度模型,表達(dá)式為

式中,φc為臨界孔隙度;Kdry為干巖石的體積模量; μdry為干巖石的剪切模量;Km為固體礦物基質(zhì)的體積模量;μm為礦物基質(zhì)的剪切模量。

將式(3）、(4）帶入式(1）,可建立彈性阻抗與流體體積模量之間的關(guān)系為

式中,Kf0、fm0、ρ0和φ0分別定義為Kf、fm、ρ和φ的平均值;標(biāo)準(zhǔn)化因子EI0的具體表達(dá)式為

利用方程(5）對(duì)4個(gè)角度的部分角度疊加道集分別進(jìn)行彈性阻抗反演,得到流體彈性阻抗后聯(lián)立4個(gè)角度的阻抗方程即可得到流體體積模量

Kf。

圖5為某研究區(qū)反演得到的流體體積模量Kf剖面(圖中所投曲線為測(cè)井解釋柱狀圖,紅色表示氣層,藍(lán)色表示水層,白色表示泥巖）。其中2.57 s與2.61 s附近發(fā)育兩套砂巖,測(cè)井資料顯示2.57 s處砂巖含氣,而2.61 s處砂巖含水。該地區(qū)的油氣藏屬典型的巖性-構(gòu)造圈閉,但由于受古地形影響,下覆含水砂巖孔隙度高于上覆含氣砂巖的孔隙度,在流體識(shí)別中易造成含流體異常假象。為克服孔隙度對(duì)流體識(shí)別造成的假象,在該工區(qū)可使用Kf作為一種更為敏感的流體因子進(jìn)行儲(chǔ)層流體識(shí)別。通過(guò)分析反演結(jié)果可知,Kf與測(cè)井解釋結(jié)果吻合較好,較為準(zhǔn)確地反映出了井周圍儲(chǔ)層含流體特征及分布情況,從而說(shuō)明了流體體積模量參數(shù)在該工區(qū)流體識(shí)別中的優(yōu)勢(shì)。

圖5 流體體積模量反演結(jié)果Fig.5 Inverted fluid bulk modulus

2 基于頻率信息的流體因子

巖石物理實(shí)驗(yàn)和實(shí)際地震資料證明,地震波在地下介質(zhì)中傳播發(fā)生強(qiáng)衰減的過(guò)程會(huì)伴隨能量衰減出現(xiàn)速度頻散現(xiàn)象,將速度頻散程度表征為頻散屬性,可以將其作為流體因子用于儲(chǔ)層流體識(shí)別。

類比于地震波長(zhǎng)尺度的“宏觀巖石物理模型”與粒間孔隙尺度的“微觀巖石物理模型”,遠(yuǎn)小于地震波長(zhǎng)卻遠(yuǎn)大于孔隙顆粒的中間尺度的巖石物理模型稱為“中觀尺度巖石物理理論”。中觀巖石物理模型對(duì)于低頻段地震波速度頻散問(wèn)題有較好的詮釋,以此為基礎(chǔ)研究滲透率、含水飽和度以及非均勻性等因素對(duì)速度頻散的影響,可為儲(chǔ)層流體識(shí)別提供必要的理論依據(jù)。

在此使用Carcione等人在2006年提出的周期疊置中觀White模型。為了研究介質(zhì)孔隙中的流體類型(即含水飽和度）對(duì)地震波速度頻散的影響,在保持其他參數(shù)不變的前提下,改變含水與含氣單元體的比重,計(jì)算得到的縱波相速度的變化趨勢(shì),結(jié)果如圖6所示。從圖中可以看到,在地震頻帶范圍內(nèi),縱波速度頻散的程度隨著含水飽和度的降低而減弱,即速度頻散的臨界頻率隨含氣量的增加而移向高頻。通過(guò)數(shù)值比較發(fā)現(xiàn),隨著含水飽和度的降低,介質(zhì)的低頻極限速度先降低再增加,這與零頻率極限情況下的縱波速度變化趨勢(shì)一致,主要原因即縱波速度受介質(zhì)模量參數(shù)與密度參數(shù)的綜合影響,含氣量達(dá)到一定程度之后,密度的變化幅度強(qiáng)于模量參數(shù)的變化幅度,且儲(chǔ)層含氣之后其速度頻散程度要比低頻極限的縱波速度更為敏感。

圖6 縱波相速度隨含水飽和度的變化趨勢(shì)Fig.6 Variation of P-wave phase velocity with water saturation

考慮到疊前地震資料包含更加豐富的振幅和頻率信息,根據(jù)Wilson等[9]提出的反射系數(shù)構(gòu)建方式,從Shuey兩項(xiàng)反射系數(shù)近似公式出發(fā),可以推導(dǎo)出包含表征縱波速度頻散程度和頻散程度隨偏移距變化梯度的兩個(gè)頻散屬性的反射系數(shù)近似公式,建立相應(yīng)的反演方程。

假設(shè)速度頻散導(dǎo)致縱波速度隨頻率發(fā)生變化,而密度不受頻率影響,則考慮速度頻散效應(yīng),對(duì)兩項(xiàng)Shuey近似公式關(guān)于頻率項(xiàng)f進(jìn)行一階泰勒展開,得到如下公式(假設(shè)f0是地震記錄的主頻）：

式中,DVP為縱波速度頻散程度;DG借鑒AVO梯度的意義表征縱波頻散程度隨偏移距的變化梯度,DVP和DG即待反演的頻散屬性參數(shù)。

對(duì)頻散屬性進(jìn)行反演之前首先需要得到不同頻帶的疊前道集信息,采用連續(xù)小波變換的分頻方法對(duì)疊前地震道集進(jìn)行時(shí)頻分析,選擇合適的優(yōu)勢(shì)頻帶后進(jìn)行分頻處理,得到相應(yīng)頻帶的疊前道集。

假設(shè)m個(gè)偏移距,n個(gè)采樣點(diǎn)和l個(gè)頻率的情況,并將矩陣進(jìn)行塊化處理,得到反演矩陣：

結(jié)合小波變換的基函數(shù)與原始地震子波,利用卷積運(yùn)算的線性性質(zhì)構(gòu)建不同頻率地震信息的子波矩陣,引入反演過(guò)程,得到如下方程：

采用最小二乘的反演方法求解式(9）,便可以得到每個(gè)采樣點(diǎn)上的DVP和DG屬性。

圖7為在某工區(qū)利用基于疊前反演結(jié)果計(jì)算的Russell流體因子剖面。根據(jù)測(cè)井解釋柱狀圖(其中,紅色表示氣層,綠色表示油層,藍(lán)色表示水層,白色表示泥巖）可以看到,2.61 s和2.64 s附近的含油氣砂巖儲(chǔ)層顯示較為明顯的低值異常。但是,從圖中可以看到,深度大于2.6s的砂體的數(shù)據(jù)區(qū)間普遍偏低,特別是2.64 s儲(chǔ)層的下傾地層表現(xiàn)為較為明顯的低值異常,依靠單一的Russell流體因子無(wú)法對(duì)其進(jìn)行有效的油氣檢測(cè)。

圖8是利用頻變AVO反演得到的頻散屬性剖面。與測(cè)井解釋結(jié)果(各顏色代表含義同圖7）進(jìn)行對(duì)比可以看到,2.61 s和2.64 s附近的兩套含油氣砂巖具有較為明顯的頻散異常顯示,且與測(cè)井解釋結(jié)果有較好的匹配,而在2.64 s儲(chǔ)層下覆地層位置未出現(xiàn)明顯的頻散異常區(qū)域,這與地質(zhì)認(rèn)識(shí)是一致的,進(jìn)一步降低了含油氣預(yù)測(cè)的多解性。從圖中還可以發(fā)現(xiàn),與常規(guī)衰減特征屬性不同的是,圖8所示的頻散屬性可以較為清晰地劃分儲(chǔ)層的縱向分布,上下邊界較清楚,其主要原因即頻散屬性在反演過(guò)程中消除了子波的帶通濾波效應(yīng),其分辨率比與頻譜能量有關(guān)的衰減特征屬性更高。

圖7 Russell流體因子剖面Fig.7 Russell fluid factor section

圖8 頻散屬性剖面Fig.8 Dispersion-dependent attribute sections

3 結(jié)束語(yǔ)

利用地震資料研究巖石孔隙單元所貯存的流體類型,主要采用的方式是在巖石物理理論指導(dǎo)下將與孔隙流體有關(guān)的異常特性表征為流體因子。以Gassmann理論為基礎(chǔ),建立了直接反演Gassmann流體項(xiàng)的方法和基于固液解耦近似的直接反演流體體積模量的方法;基于中觀巖石物理理論建立了速度頻散屬性的反演方法,這些方法在實(shí)際工區(qū)應(yīng)用中取得了良好的效果。這表明,以雙相介質(zhì)巖石物理理論為基礎(chǔ),才能獲得對(duì)于儲(chǔ)層流體有更高的敏感性的流體因子,更好地克服識(shí)別假象,最終得到精確可靠的流體識(shí)別結(jié)果。

參考文獻(xiàn)：

[1] BACKUS M M,CHEN R L.Flat spot exploration[J]. Geophysical Prospecting,1975,23(3）：533-577.

[2] OSTRANDER W J.Plane-wave reflection coefficients for gas sands at nonnormal angles of incidence[J].Geophysics,1984,49(10）：1637-1648.

[3] SMITH G C,GIDLOW P M.Weighted Stacking for Rock Property Estimation and Detection of GAS[J].Geophysical Prospecting,1987,35(9）：993-1014.

[4] GOODWAY B,CHEN T,DOWNTON J.Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters;“λρ”,μρ,λμ fluid stack”,from P and S inversions[C/OL].Expanded Abstract of 67th Annual International SEG Meeting,1997[2012-09-01]. http：//dx.doi.org/10.1190/1.188795.

[5] GASSMANN F.Uber die elastizitat poroser medien[J]. Vierteljahrsschrift der Natruforschenden Gesellschaft in Zurich,1951,96：1-23.

[6] RUSSELL B H,HEDLIN K,HILTERMAN F J,et al. Fluid-property discrimination with AVO：a Biot-Gassmann perspective[J].Geophysics,2003,68(1）：29-39.

[7] RUSSELL B H,GRAY D,HAMPSON D P.Linearized AVO and poroelasticity[J].Geophysics,2011,76(3）： C19-C29.

[8] 印興耀,張世鑫,張繁昌,等.利用基于Russell近似的彈性波阻抗反演進(jìn)行儲(chǔ)層描述和流體識(shí)別[J].石油地球物理勘探,2010(3）：373-380.

YIN Xing-yao,ZHANG Shi-xin,ZHANG Fan-chang,et al.Utilizing Russell approximation based elastic wave impedance inversion to conduct reservoir description and fluid identification[J].Oil Geophysical Prospecting,2010 (3）：373-380.

[9] WILSON A,CHAPMAN M,LI X Y.Frequency-dependent AVO inversion[C/OL].Expanded Abstract of 79th Annual International SEG Meeting,2009[2012-12-10]. http：//dx.doi.org/10.1190/1.3255572.

[10] CHAPMAN M,LIU E,LI X Y.The influence of fluidsensitive dispersion and attenuation on AVO analysis [J].Geophysical Journal International,2006,167(1）： 89-105.

[11] 吳小羊.基于頻譜分析技術(shù)的頻散AVO反演研究[D].武漢：中國(guó)地質(zhì)大學(xué)地球物理與空間信息學(xué)院,2010.

WU Xiao-yang.Frequency dependent AVO inversion using spectral decomposition techniques[D].Wuhan： Institute of Geophysics&Geomatics,China University of Geosciences,2010.

[12] WANG B L,YIN X Y,ZHANG F C.Lamé parameters inversion based on elastic impedance and its application [J].Applied Geophysics,2006,3(3）：174-178.

[13] 張世鑫.基于地震信息的流體識(shí)別方法研究與應(yīng)用[D].青島：中國(guó)石油大學(xué)地球科學(xué)與技術(shù)學(xué)院, 2012.

ZHANG Shi-xin.Methodology and application of fluid identification with seismic information[D].Qingdao： School of Geosciences,China University of Petroleum, 2012.

[14] HAN D H,BATZLE M.Gain function and hydrocarbon indicators[C/OL].Expanded Abstract of 73th Annual International SEG Meeting,2003[2011-6-15].http：// dx.doi.org/10.1190/1.1817633.

[15] HAN D H,BATZLE M.Gassmann?s equation and fluidsaturation effects on seismic velocities[J].Geophysics, 2004,69(2）：398-405.

[16] NUR A,MAVKO G,DVORKIN J,et al.Critical porosity：a key to relating physical properties to porosity in rocks[J].The Leading Edge,1998,17(3）：374-362.

(編輯 修榮榮）

Seismic fluid discrimination based on two-phase media theory

YIN Xing-yao1,LI Chao1,ZHANG Shi-xin2
(1.School of Geosciences in China University of Petroleum,Qingdao 266580,China; 2.CNOOC Research Institute,Beijing 100027,China）

To avoid the cumulative error and to enhance the accuracy of fluid discrimination,a direct extracting approach for fluid factors based on elastic impedance inversion and a novel solid-fluid decoupled way to constructing the fluid factor with poroelastic theory were proposed.Seismic velocity dispersion is persistently observed in hydrocarbon reservoirs.Based on mesoscopic scale rock physics theory,a dispersion-dependent attribute inversion method was developed for reservoir fluid discrimination by using pre-stack seismic data.This method provides quantitative inversion scheme of the dispersion-dependent attributes with high accuracy.Applications on real data show that this fluid discrimination method which combines fluid factor based on the two-phase media theory and pre-stack seismic inversion is more accurate and stable.

two-phase media;fluid discrimination;elastic impedance;pre-stack seismic inversion;dispersion-dependent attribute

P 631.4

A

1673-5005(2013）05-0038-06

10.3969/j.issn.1673-5005.2013.05.006

2013-06-30

國(guó)家”973”計(jì)劃項(xiàng)目(2013CB228604）;中國(guó)石油天然氣集團(tuán)公司科學(xué)研究與技術(shù)開發(fā)項(xiàng)目(2011A-3603）

印興耀(1962-）,男,教授,博士生導(dǎo)師,從事勘探地球物理理論與方法的教學(xué)與科研工作。E-mail：xyyin@upc.edu.cn。