雙參數C-半群

黃翠,王彩俠,張明翠,王淑莉

(中國礦業大學理學院,江蘇徐州 221008)

雙參數C-半群

黃翠,王彩俠,張明翠,王淑莉

(中國礦業大學理學院,江蘇徐州 221008)

引入單參數C-半群和雙參數C0-半群,給出了更一般的雙參數C-半群和無窮小生成元的定義,應用雙參數半群與單參數半群的關系和雙參數半群的性質,給出了雙參數C-半群的階全微分,偏微分,指數有界性,和雙參數C-半群是由C、A1和A2唯一確定的閉稠定線性算子的一個充分條件.

雙參數C-半群;全微分;偏微分;指數有界;閉稠定線性算子

1 引言

滿足某些條件的算子半群是對應抽象柯西問題(ACP)的解.目前算子半群已經被應用生物、物理、計算機、交通等領域.因此,研究一些算子半群的性質是非常必要的.前人對C0-半群的性質,擾動和逼近,穩定性已經做了很深入的研究,得到了很多有用的結果.對于更一般C-半群和雙參數C0-半群也有一些研究,但是沒有像C0-半群理論那么深入,尤其是擾動和逼近、穩定性.本文根據C-半群和雙參數C0-半群,定義更一般的雙參數C-半群,并對它的全微分和偏微分,指數有界性和閉稠定性做了詳細的研究.

2 定義和引理

定義2.5[3]設S是R中的點集,如果點集S在每個非空的開集中都不稠密,就稱S是疏朗集或稱無處稠密集.

引理2.1[3]點集S是疏朗集的充要條件是在任何開區間(α,β)中存在開區間(α′,β′)?(α,β)在開區間(α′,β′)中沒有S中的點.

引理2.2[3]疏朗集的余集一定是稠密集.

3 主要結論

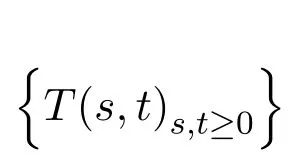
證明設映射L:R2→L(x),如果存在某個線性變換L使得(s,t)∈U(0,0)點(0,0)的某個領域時有T(s,t)-T(0,0)=L(s,t)+R(s,t),其中

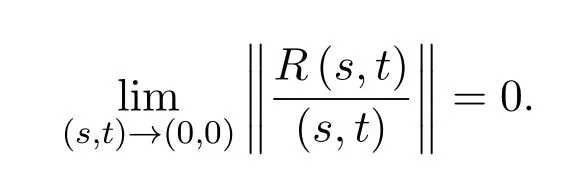
則T(s,t)作為二元函數在(0,0)處的微分dT(s,t)|(0,0)存在.

設A1、A2分別是C-半群{T(s,0)}s≥0和{T(0,t)}t≥0的無窮小生成元,令

[1]陳文忠.C-無窮小生成元的表示式[J].廈門大學學報:自然科學版,1993,32(2):135-140.

[2]Al-Sharif Sh,Khalil R.On the generator of two parameter semigroups[J].Applied Mathematics and Computation,2004,156:403-414.

[3]張鳴歧.應用泛函分析引論[M].北京:北京理工大學出版社,1989.

[4]黃永忠.算子半群與應用[M].武漢:華中科技大學出版社,2011.

[5]Li Y C,Shaw S Y.On characterization and perturbation of local C-semigroups[J].Proceedings of the American Mathematical Society,2007,1(1):1097-1106.

[6]Shaw S Y,Kuo C C.Generation of local C-semigroups and solvability of the abstract Cauchy problems[J]. Taiwanese Journal of Mathematicas,2005,9(2):291-311.

[7]陳闖,宋曉秋,李曉敏.C-半群Lyapunov方程的自伴解與穩定性[J].南京大學學報:數學半年刊,2008,25(1): 86-93.

[8]宋曉秋.應用泛函分析[M].徐州:中國礦業大學出版社,2013.

Two parameter C-semigroups

Huang Cui,Wang Caixia,Zhang Mingcui,Wang Shuli

(College of Science,China University of Mining and Technology,Xuzhou221008,China)

According to the C-semigroup and two parameter C0-semigroups,this paper gives the definition of a more general two-parameter C-semigroup,infinitesimal generator,two parameter C-semigroup′s total differential and partial differential.It is exponentially bounded.With the complement of C-semigroup′s domains lichtung setes,proof the two parameter C-semigroups is uniquely determined by the C,A1and A2,whose infinitesimal generator is densely defined and closed linear operator.

two parameter C-semigroups,total differential,partial differential,exponentially bounded, densely defined and closed linear operator

O177.2

A

1008-5513(2013)03-0299-07

10.3969/j.issn.1008-5513.2013.03.012

2012-11-06.

高水平論文專項基金(2012LWB53).

黃翠(1986-),碩士生,研究方向：泛函分析與應用泛函分析.

2010 MSC:47A62