對稱串聯型非接觸電能傳輸系統頻率分裂現象的頻域分析
李鳳娥,牛王強
(1.上海民航職業技術學院 民航工程系,上海 200232;
2.上海海事大學 航運技術與控制工程交通行業重點實驗室,上海 201306)
0 引言
非接觸電能傳輸(Contactless Power Transfer,CPT)在交通運輸[1]、醫學[2]等領域有著重要應用.文獻[3]報道CPT 技術在機載雷達上的應用.傳統機載雷達利用滑環為其供電.滑環易發生機械磨損、易產生電弧、需頻繁維修.采用CPT 技術為機載雷達供電可克服上述缺點,提高雷達供電系統的可靠性,延長雷達系統工作壽命,減少系統維修次數.
頻率分裂現象是CPT 系統的重要現象之一.[4]CPT 系統的頻率分裂現象[2,4-6]是指當一次側和二次側之間的耦合因數大于某臨界值時,負載電壓從單峰曲線變化為雙峰曲線.代數方法[4,7]是研究頻率分裂現象的方法之一,其優點是可以精確給出頻率分裂臨界點和分裂頻率,缺點是相關表達式較復雜,物理意義不明確.傳遞函數的Bode 頻域分析可以清晰給出系統各個子環節的貢獻.[8-9]本文利用Bode 方法分析對稱串聯型CPT 系統的頻率分裂現象,指出頻率分裂現象是由兩個二階振蕩環節的諧振引起的.
1 方 法
1.1 電路模型
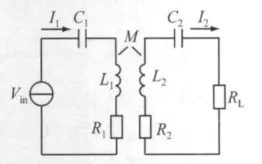
圖1 CPT 系統的電路模型
串聯型CPT 系統的電路模型見圖1.
一次側的回路阻抗[7,10]
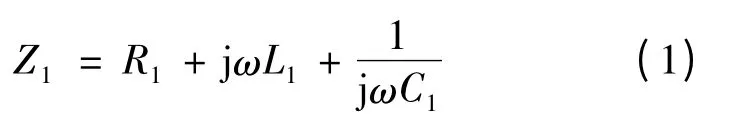
二次側的回路阻抗
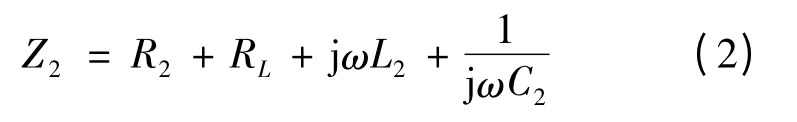
二次側反射到一次側的阻抗

耦合因數

一次側電流

負載電壓
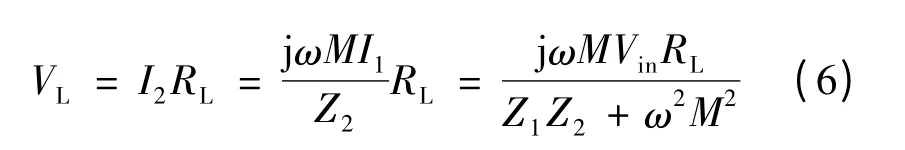
1.2 頻率分裂現象
CPT 系統的頻率分裂現象是指:耦合因數k從0 開始逐漸增大,當k 大于頻率分裂臨界點時,負載電壓從單峰曲線變化為雙峰曲線.[4]圖2 給出對稱CPT系統負載電壓與系統頻率和k 的關系,CPT 系統的參數取值見表1.該系統的頻率分裂臨界點是ksplit=0.23.當k >0.23 時,負載電壓分裂出兩道脊.大于自然諧振頻率90.79 kHz 的分裂脊峰值頻率對應偶分裂頻率,小于自然諧振頻率的分裂脊峰值頻率對應奇分裂頻率.[11]
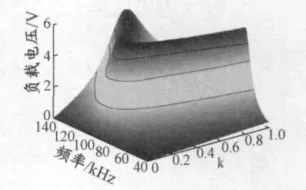
圖2 對稱CPT 系統的頻率分裂現象
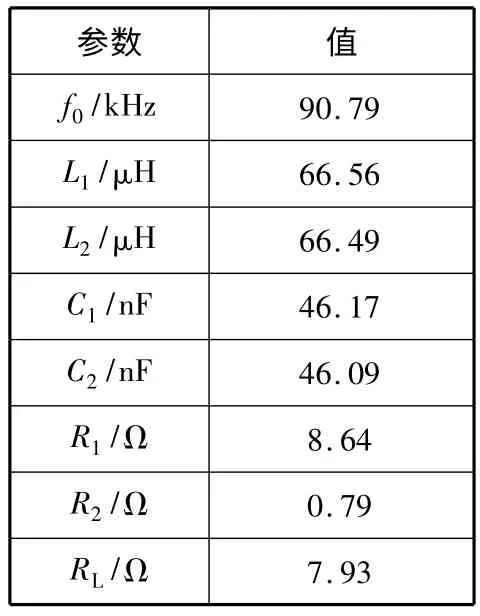
表1 CPT 系統參數值
1.3 Bode 分析
1.3.1 系統傳遞函數
令s=jω,則式(6)的負載電壓[5]
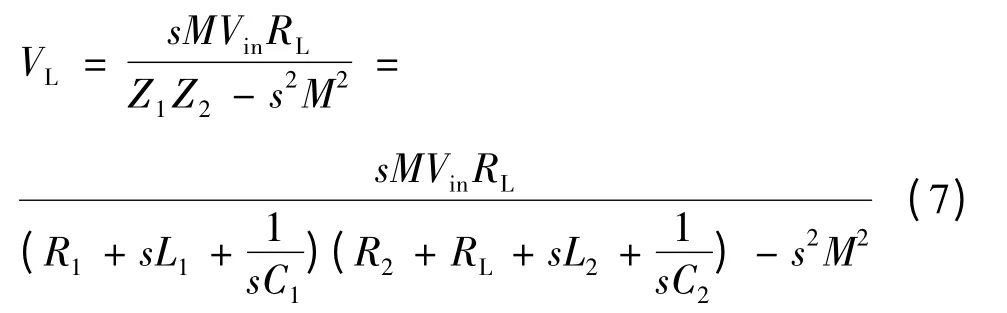
在對稱CPT 系統中,有L=L1=L2,C=C1=C2,R=R1=R2+RL.令
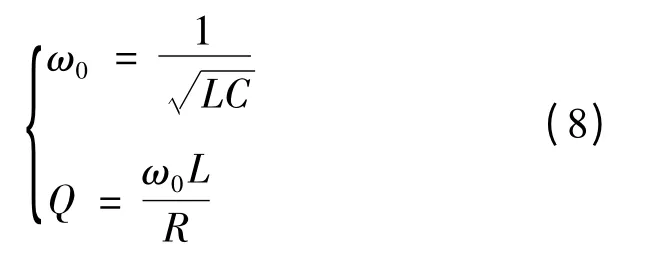
這時,負載電壓

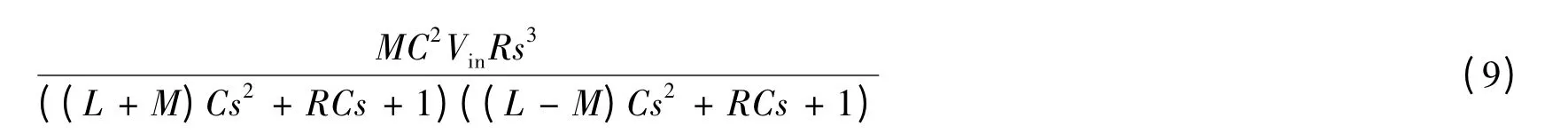
令
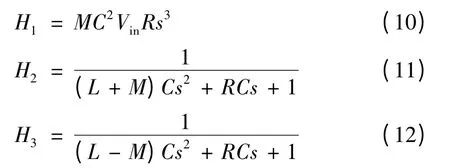
則
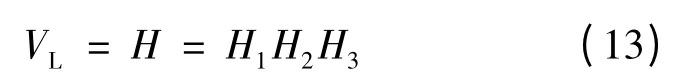
負載電壓VL由3個環節組成:1個三階微分環節H1和2個二階振蕩環節H2,H3.二階振蕩環節在低阻尼時會產生比較大的諧振峰值.
1.3.2 數值例子
L=L1,C=C1,R=R1的取值見表1.這時,系統H 的自然諧振頻率是ω0=90.79 kHz,品質因數是Q=4.4,頻率分裂臨界點是ksplit=0.23.
取k=0.489 >ksplit,則H 出現頻率分裂.H 各個環節的頻率響應見圖3.H2和H3都出現諧振,且諧振頻率都在H的分裂頻率附近.
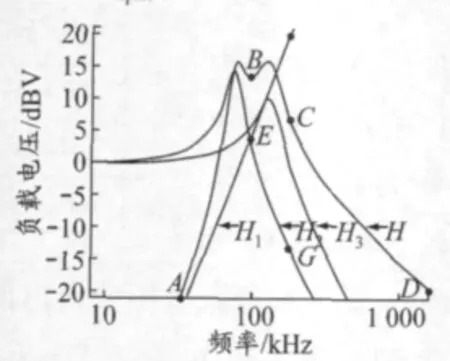
圖3 對稱CPT 系統的Bode 圖
在A 點左側,H2和H3比較小,H≈H1,近似為60 dB/10 倍頻程的直線;
在區間(A,B),H3較小,H2出現諧振,諧振頻率73.75 kHz,H2和H1的和產生H 的奇分裂頻率峰值,奇分裂頻率為76.1 kHz;
在區間(B,C),H1的斜率是60 dB/10 倍頻程,H2的斜率約為-60 dB/10 倍頻程,求和后H2與H3幾乎抵消,H 的特性主要由H3決定,而H3出現諧振,故H 的偶分裂頻率主要由H3的諧振頻率決定.特別地,H1曲線從E 點到F 點改變16.13 dB,H2曲線從E 點到G 點改變-16.99 dB,求和后為-0.86 dB.H3的諧振頻率是123.77 kHz,H 的偶分裂頻率是123.8 kHz.
在區間(C,D),H1的斜率是60 dB/10 倍頻程,H2和H3的斜率約為-40 dB/10 倍頻程,求和后H的斜率約為-20 dB/10 倍頻程.
由以上分析可知,H 的頻率分裂現象主要是由H2和H3的諧振產生的.H2的諧振頻率距離H 的奇分裂頻率較遠,是由于H1與H3在諧振峰值附近不能抵消.H3的諧振頻率與H 的偶分裂頻率幾乎重合,是由于H1與H2在諧振峰值附近的抵消.
1.3.3 理論分析

由以上理論分析和數值仿真可知,H2和H3的諧振頻率可以作為H 奇偶分裂頻率的估計.H2的諧振頻率[8-9]
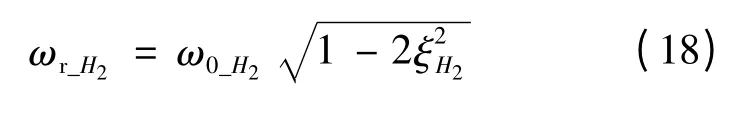
H3的諧振頻率
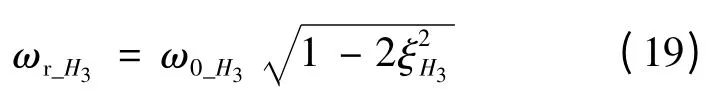
當ksplit_Bode=0 時,Bode 意義下的臨界分裂頻率
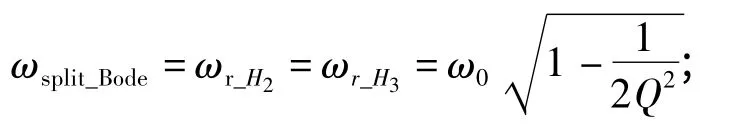
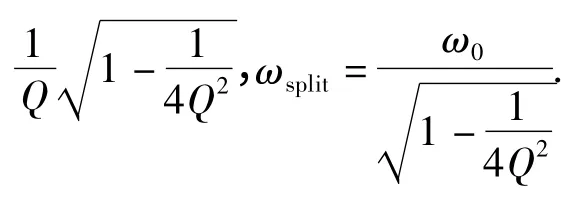
故以上的Bode 分析有助于理解頻率分裂的物理意義,抓住頻率分裂定性特性,但是計算出的頻率分裂臨界點和分裂頻率都是近似值.
2 實驗結果
為了驗證前文的分析,搭建1個10 W 的對稱CPT 系統.系統由2個平面螺旋線圈構成,螺旋的外徑是20 cm,內徑是12 cm,導線選取AWG16 多芯線.系統的關鍵參數見表1,參數值用LCR821 測試儀測定.
利用信號發生器(Tektronix:AFG3102)產生標準的正弦波信號,該信號經過10 W 的功率放大器(Rigol:PA1011)放大后給CPT 系統一次側線圈.利用示波器(Rigol:DS1302)記錄CPT 系統二次側的負載電壓.
圖4 給出對稱CPT 系統的頻率分裂特性.(0,0.23)是非頻率分裂區,0.23是頻率分裂臨界點,(0.23,1)是頻率分裂區.圓點是實測的偶分裂頻率,方塊點是實測的奇分裂頻率,菱形點是頻率分裂前的實測峰值頻率.
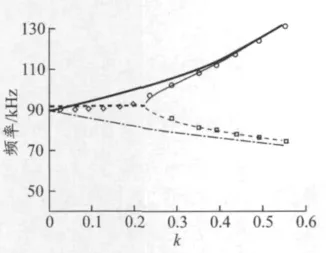
圖4 對稱CPT 系統的頻率分裂特性
細實線是利用代數方法計算出的理論偶分裂頻率,也是圖2 的左側分裂脊線;細虛線是理論奇分裂頻率,也是圖2 的右側分裂脊線;粗虛線是頻率分裂前的理論峰值頻率.
H2和H3的諧振頻率是H 奇偶分裂頻率的Bode 估計值.粗實線是式(19)給出的H3環節諧振頻率,點劃線是式(18)給出的H2環節諧振頻率.在頻率分裂區,粗實線、點劃線與細實線、細虛線的趨勢一致.越靠近頻率分裂臨界點,Bode分析給出的分裂頻率誤差越大.在頻率分裂臨界點,粗實線(H3)給出的分裂頻率誤差是10.7%,點劃線(H2)給出的分裂頻率誤差是-11.6%.越遠離頻率分裂臨界點,Bode 分析給出的分裂頻率誤差越小.而且,H3比H2給出的分裂頻率誤差小,這一點與圖3 的分析一致.
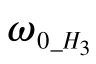
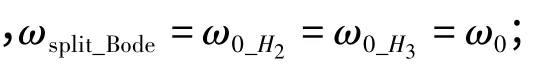
3 討 論
對稱CPT 系統的應用見最大功率傳輸技術[12],以及一次側和二次側的雙向電能傳輸技術[13-14].
對稱CPT 系統Bode 分析的關鍵一步是式(7)分母的四階系統,在一次側和二次側參數對稱時,正好可以因式分解為兩個二階系統的乘積.在非對稱的一般CPT 系統,式(7)分母的四階系統一般不能寫成兩個二階系統的乘積.盡管Bode 分析不能直接用于一般CPT 系統頻率分裂現象的分析,它也可以為一般CPT 系統的頻率分裂現象分析提供新的思路.
4 結束語
利用Bode 頻域分析方法考察對稱CPT 系統3個子環節的貢獻,定性指出對稱串聯型CPT 系統的頻率分裂現象是由兩個二階振蕩環節的諧振引起的.而且兩個二階振蕩環節的諧振頻率可以作為對稱串聯型CPT 系統奇偶分裂頻率的定性估計.
[1]SALLAN J,VILLA J L,LLOMBART A,et al.Optimal design of ICPT systems applied to electric vehicle battery charge[J].IEEE Trans on Industrial Electron,2009,56(6):2140-2149.
[2]CHEN Q H,WONG S C,TSE C K,et al.Analysis,design,and control of a transcutaneous power regulator for artificial hearts[J].IEEE Trans on Biomedical Circuits & Systems,2009,3(1):23-31.
[3]PAPASTERGIOU K D,MACPHERSON D E.An airborne radar power supply with contactless transfer of energy-Part I:rotating transformer[J].IEEE Trans on Industrial Electron,2007,54(5):2874-2884.
[4]SAMPLE A P,MEYER D A,SMITH J R.Analysis,experimental results,and range adaptation of magnetically coupled resonators for wireless power transfer[J].IEEE Trans on Industrial Electron,2011,58(2):544-554.
[5]BAKER M W,SARPESHKAR R.Feedback analysis and design of RF power links for low-power bionic systems[J].IEEE Trans on Biomedical Circuits & Systems,2007,1(1):28-38.
[6]MORADEWICZ A J,KAZMIERKOWSKI M P.Contactless energy transfer system with FPGA-controlled resonant converter[J].IEEE Trans on Industrial Electron,2011,57(9):3181-3190.
[7]WANG C S,COVIC G A,STIELAU O H.Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems[J].IEEE Trans on Industrial Electron,2004,51(1):148-157.
[8]OGATA K.Modern Control Engineering[M].New Jersey:Prentice-Hall,Inc.,2002.
[9]胡壽松.自動控制原理[M].北京:國防工業出版社,1994.
[10]牛王強,沈愛弟,顧偉,等.可變負載非接觸電能傳輸系統的無功功率補償[J].上海海事大學學報,2011,32(1):49-53.
[11]KIM Y,LING H.Investigation of coupled mode behaviour of electrically small meander antennas[J].Electron Letters,2007,43(23):1250-1252.
[12]LI H L,HU A P,COVIC G A,et al.Optimal coupling condition of IPT system for achieving maximum power transfer[J].Electron Letters,2009,45(1):76-77.
[13]MADAWALA U K,THRIMAWITHANA D J.Current sourced bi-directional inductive power transfer system[J].IET Power Electron,2011,4(4):471-480.
[14]戴欣,孫躍,蘇玉剛,等.非接觸電能雙向推送模式研究[J].中國電機工程學報,2010,30(18):55-61.

