連續型隨機變量函數概率密度的教學方法探討
孫春香
(淮南師范學院 數學與計算科學系,安徽 淮南 232001)
連續型隨機變量函數概率密度的教學方法探討
孫春香
(淮南師范學院 數學與計算科學系,安徽 淮南 232001)
本文從單個隨機變量的函數和兩個隨機變量的函數的概率分布兩種情形分別探討隨機變量函數的概率密度的求解方法.
隨機變量;密度函數;隨機變量函數;卷積公式
1 引言
隨機變量函數的分布問題是概率論與數理統計中的一項重要的問題,它在隨機變量研究中占有非常重要的意義,是整個隨機變量研究的核心內容,關于許多隨機變量的研究都是通過研究隨機變量函數的分布問題得以發展.因此,在這部分的學習中,掌握其方法和解題技巧至關重要.以下就是作者憑借多年從事概率統計課程教學的經驗總結了幾點看法.
2 單個隨機變量函數的密度函數的求法
對于這種類型的問題,主要通過某個隨機變量的密度函數f(x)來找出Y=g(X)的密度函數f Y(y),主要介紹一下兩種方法.
2.1 “分布函數法”——求解問題的萬能公式
“分布函數法”是解決隨機變量函數的密度函數的一般方法,可以賦予其“萬能公式”的稱號.其原因是不管y=g(x)的形式多么復雜,均可采用此方法.具體步驟如下:
(1)先由X的值域ΩX,確定出Y=g(x)的值域ΩY;
注1:所謂值域通常指的是隨機變量密度函數表達式的非零區間.
(2)對于任意的y∈ΩY,Y的分布函數
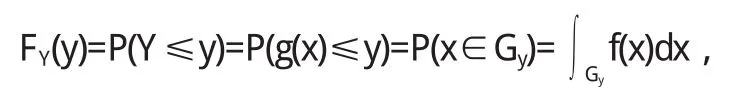
(其中G y={x|g(x)≤y});
(3)寫出FY(y)在(-∞,+∞)上的表達式;
(4)求導得到f(y)=Fy'(y).
例1已知X-N(0,1),試求Y=2 X2+1的密度函數f(y).
解 由已知得X的密度函數為
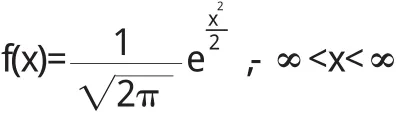
易知隨機變量X的非零區間為ΩX=(-∞,+∞),
從而由Y=2 X2+1≥1得到ΩY=(1,+∞),
所以當y≤1時Fy(y)=0
當y>1時,F Y(y)=P(Y≤y)=P(2 X2+1≤y)
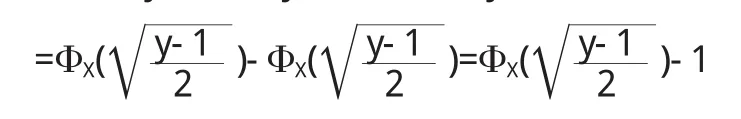
所以當y>1時,兩邊對y求導數得到
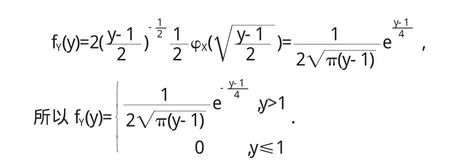
注2:在非零區間上找分布函數時,不一定求出其具體的表達式,因為在以上問題中,我們的目的是求出Y的密度函數,分布函數只是一個中間過渡,可運用X的分布函數給出Y的分布函數的形式表達式,利用復合函數求導可以直接給出其密度函數,這樣在很多類似問題中可使問題簡單化.
2.2 特殊求解——公式法
當g(x)為嚴格單調時,可運用以下定理直接得出結論.
定理1設X是連續隨機變量,其密度函數為fX(x).Y=g (X)是另一個隨機變量.若y=g(x)嚴格單調,其反函數h(y)有連續導函數,則Y=g(x)的密度函數為
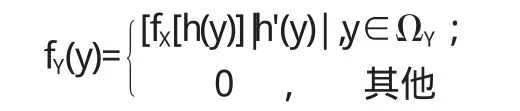
其中ΩY為隨機變量Y的非零區間.
證明 見參考文獻[1].
例2設X-N(μ,σ2),求Y=3 X+2的概率密度函數.
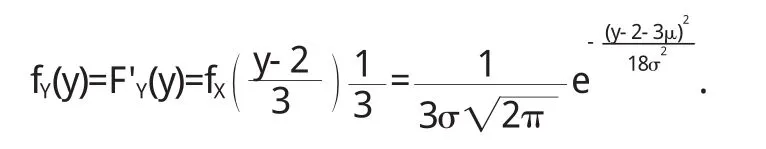
注3:通過例題可以看出運用定理1解決問題很是簡便,但是要注意其適用的條件,這點在學習中容易被忽視.例如讀者可以考慮當X-U(0,π)及時Y=s i n X的密度函數的求解方法的異同.
由定理1,對于正態分布,還有如下結論
定理2設隨機變量X服從正態分布N(μ,σ2),則當a≠0時,有Y=a X+b-N(a μ+b,a2σ2).
證明 當a>0時,Y=a X+b是嚴格增函數,仍在(-∞, +∞)上取值,其反函數為X=(Y-b)/a,由定理可得
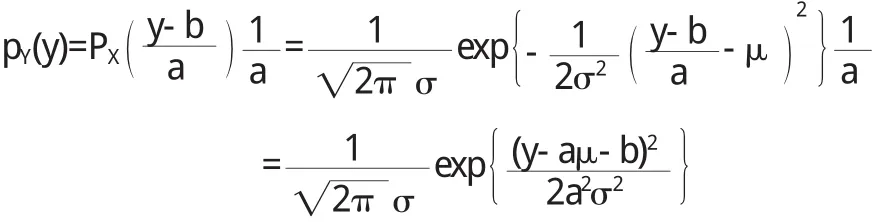
這就是正態分布N(μ+b,a2σ2)的密度函數.
當a<0時,Y=a X+b是嚴格減函數,仍在(-∞,+∞)上取值,其反函數為X=(Y-b)/a,由上定理可得
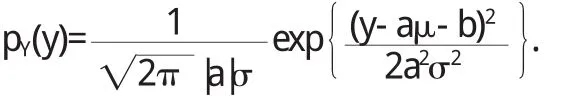
這是正態分布N(a μ+b,a2σ2)的密度函數,結論得證.
這個定理表明,正態變量的線性變換仍為正態變量,其數學期望和方差可直接從線性變換求得.若取a=1/σ,b=-μ/σ,則Y=a X+b-N(0,1).這在概率論與數理統計中意義重大.
例3設隨機變量X-(10,22),試求Y=3 X+5的分布.
解 由定理2知Y仍是正態變量,其數學期望和方差分別為
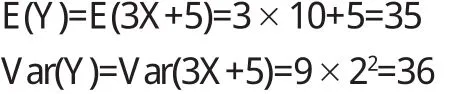
所以Y=3 X+5的分布為N(3 5,62).
3 兩個連續隨機變量的函數的密度函數的求法
這部分涉及到的問題和第二節的問題極其類似,只是把一維的問題推廣到二維當中去,因此,解決的方法也極其類似.
3.1 “分布函數法”——求解問題的萬能公式
若已知(X,Y)的聯合概率密度為f(x,y),欲求Z=g(X,Y)的概率密度fZ(z),解決此類問題仍然采用以下4步:
(1)先由(X,Y)的值域確定出Z=g(X,Y)的值域ΩZ;
(2)對于任意的z∈ΩZ,求出Z=g(X,Y)的分布函數;
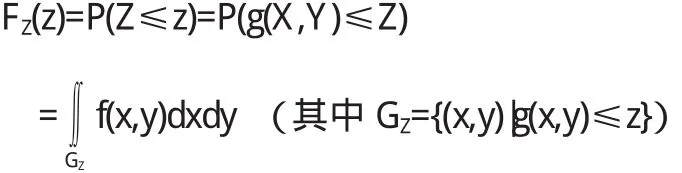
(3)FZ(z)寫出 在整個坐標平面上的表達式;
(4)求導,即可得Z=g(X,Y)的概率密度
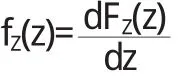
通常,我們也稱這種方法為“分布函數法”,它適用于任何一種函數形式下Z=g(X,Y)的密度函數的求解,是前面“分布函數法”的推廣.
當z<0時,FZ(z)=0,
當z>0時,FZ(z)=P(Z≤z)
所以FZ(z),兩邊對z求導數得
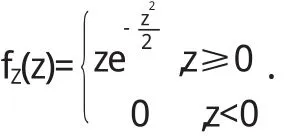
3.2 特殊求解——公式法
“分布函數法”雖然能解決所有的問題,但因為涉及到二重積分的計算問題,操作起來相當復雜.因此,對于常見的和、差的分布,商的分布,乘積的分布給出下面的求解公式.
定理3已知(X,Y)的聯合概率密度為f(x,y),則
(1)Z=X++Y的密度函數

(2)Z=X-Y的密度函數

(3)Z=X/Y的密度函數

(4)Z=X Y的密度函數
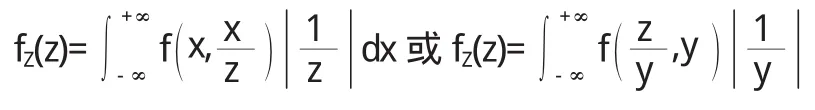
d x其中(1)和(2)分別稱為和、差的卷積公式.
解 由卷積公式
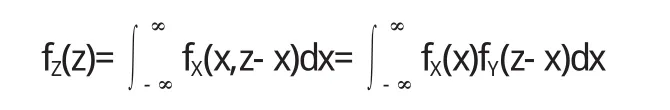
為確定積分限,先找出使被積函數不為0的區域

注4:通過上面例5可以看出,運用公式過程相對簡單,但在確定分段函數的非零區間時,需要解出一個含參數的不等式組,值得讀者特別關注,這也是公式法的不足之處.
4 小結
本文所得出的結論對隨機變量函數的學習具有一定的指導意義,雖然現有對隨機變量函數的研究已經比較成熟,但要想對隨機變量函數有更深一步的認識,還有待于進一步的發展.
〔1〕盛驟,等.概率論與數理統計[M].高等教育出版社,2008.〔2〕茆詩松,程依明,濮曉龍.概率論與數理統計教程[M].高等教育出版社,2004.
〔3〕陳仲堂.趙德平.概率論與數理統計[M].高等教育出版社,2012.
〔4〕張菊芳,陳寧,章曉,等.概率論與數理統計[M].化學工業出版,2011.
〔5〕唐興蕓,羅明燕.二維連續型隨機變量函數的概率密度[J].黔南民族師范學院學報,2012(2):112-115.
〔6〕崔靜.關于一維與二維連續型隨機變量函數的分布探討[J].西安文理學院學報,2007(10):32-36.
G642
A
1673-260 X(2013)10-0227-0 2
安徽省高等學校優秀人才基金研究項目資助(2011SQRL136);淮南師范學院教學研究項目資助(2012hssjk10)

