基于相空間重構(gòu)的獨立分量分析及其工程應(yīng)用

趙長生，姜立勇，蔡娟，李文華，林琪超

(1.山推工程機(jī)械股份有限公司，山東 濟(jì)寧 272073；2.濟(jì)南時代試金試驗機(jī)有限公司，濟(jì)南 250300)

獨立分量分析(ICA)是一種高階統(tǒng)計量方法，能夠從受噪聲干擾的信號中提取微弱的有用信息，已被廣泛應(yīng)用在語音信號、生物信號、機(jī)械故障診斷[1]等領(lǐng)域中，并取得了較好的效果。在機(jī)械振動信號分析中，由于ICA固有的特點，需要信道個數(shù)大于或等于信源個數(shù)，常規(guī)做法是同時設(shè)置多個傳感器進(jìn)行信號采集，然后對多通道信號進(jìn)行ICA，從混合振動(或聲音)信號中恢復(fù)出獨立信源，然后對感興趣的分量進(jìn)行分析，實現(xiàn)有用信息的提取[2]。在實際機(jī)械故障信號的采集時，為滿足ICA要求，通常的方法是增加傳感器(信道)個數(shù)，然而這種方法并非完美：一方面，若增加的傳感器個數(shù)不合理，會帶來欠定或超定問題，同時也可能引起時延現(xiàn)象；另一方面，增加傳感器個數(shù)也會帶來信號采集成本的增加。基于此，許多文獻(xiàn)提出了基于單通道信號的ICA改進(jìn)方案，如基于外加“虛擬通道”[3-4]、基于“先驗知識”[5]等單通道ICA特征提取或降噪方法，前者在工程信號分析中應(yīng)用較廣，后者多用在語音信號分離中。基于相空間重構(gòu)的ICA方法已在信號降噪方面得到成功應(yīng)用[6]，因此，嘗試將其引入滾動軸承故障特征提取中，研究運用相空間重構(gòu)和ICA相結(jié)合的方法提取滾動軸承周期性的故障沖擊信息。

1 基礎(chǔ)理論

1.1 相空間重構(gòu)

相空間重構(gòu)技術(shù)是一種時間序列分析方法。對于一維時間序列，運用相空間重構(gòu)技術(shù)，可以將其擴(kuò)展到高維相空間，并從高維相空間中恢復(fù)出包含系統(tǒng)分量信息的吸引子，重構(gòu)后的相空間具有與原系統(tǒng)相同的動力學(xué)特性。相空間重構(gòu)技術(shù)是一種非線性問題處理方法，而機(jī)械故障的沖擊信息正是一種典型的非線性時間序列，所以將相空間理論引入滾動軸承故障沖擊信號的重構(gòu)中是合理的。

對于給定時間序列x=xn,n=1,2,...，N，當(dāng)選擇好時間延遲τ和嵌入維數(shù)d后，依據(jù)相空間重構(gòu)理論，可以得到能夠反映該時間序列特性的動力系統(tǒng)軌道矩陣，Y=[xi,xi+τ,xi+2τ，...，x1+(d-1)τ],i=1,2，...，N-(d-1)τ。

在相空間重構(gòu)中，時間延遲及嵌入維數(shù)的選擇非常重要，直接決定著相空間矩陣能否真實地反映隱含在時間序列中的非線性規(guī)律和動力學(xué)特征，同時也間接影響后續(xù)ICA特征提取效果。在此，選取交互信息方法[7]和偽臨近點方法[8]計算時間序列的最佳延遲和最佳嵌入維數(shù)。一般選擇交互信息方法中第1次出現(xiàn)極小值時的τ值作為最佳延遲，選取當(dāng)位數(shù)比變化緩慢趨于直線時的轉(zhuǎn)折點的值作為最佳嵌入維數(shù)。

1.2 獨立分量分析

ICA的簡單框圖如圖1所示。X為多個信源S經(jīng)混合矩陣A組合而成(X=AS)。ICA的目的就是在S與A未知的前提下，求解一個解混矩陣B，使X通過它后所得的輸出矩陣Y是S的最佳逼近。關(guān)于矩陣B的計算，選取實際應(yīng)用中較為成熟的基于負(fù)熵的“固定點算法”——快速ICA算法(FICA)。此方法不僅收斂速度較快，而且在迭代過程中無需引入人為設(shè)置的參數(shù)。對于時間序列x進(jìn)行FICA的步驟如下：

圖1 ICA簡單框圖

(1)對序列x去均值；

(2)白化x，得到矩陣z；

(3)任意選取令‖ui(0)‖2=1的初值ui(0)；

(6)判斷是否收斂,若收斂則結(jié)束，否則,返回步驟(4)。

經(jīng)ICA分離出的時間序列，各分量的相位、幅值、信息已失真，順序也具有某種不確定性，因而這些都不能作為特征提取參數(shù)，而隱含在序列中的周期性故障沖擊規(guī)律和頻域信息均沒有改變，所以對經(jīng)ICA分離出的獨立分量進(jìn)行周期性故障沖擊提取和頻域分析是可行的。

2 方法實現(xiàn)

由于EMD本身有對噪聲敏感的缺陷,使得基于“EMD-虛擬通道”的升維方法在背景噪聲較大時分解效果不佳；引入虛擬噪聲通道的升維方法需要引入的噪聲與某混合信號本身包含的噪聲一樣(或近似)才能較好地消除該混合信號含有的噪聲，當(dāng)干擾噪聲類型未知時，需嘗試多種噪聲類型。因此，需要對背景噪聲了解使得這種方法在實際應(yīng)用中受到很大限制；基于“先驗知識”的單通道ICA分離效果對基函數(shù)的選擇有較大的依賴性。相空間重構(gòu)技術(shù)不但可以對一維信號升維，而且重構(gòu)后的相空間矩陣能夠反應(yīng)隱含在時間序列中的非線性規(guī)律和動力學(xué)特征。ICA方法具有盲信號處理特性，能夠很好地消除相空間矩陣分量之間的互相關(guān)信息和冗余信息，使得隱藏在混合信號中的信源盡可能獨立地分離出來。基于此，設(shè)計了一種基于相空間重構(gòu)和獨立分量分析相結(jié)合的單通道新信號特征提取方法，主要步驟如下：

(1)確定最佳延時和嵌入維數(shù)；

(2)相空間重構(gòu)；

(3)對重構(gòu)相空間矩陣進(jìn)行ICA；

(4)提取特征信息。

3 仿真分析

為了驗證該方法的有效性，原始單通道仿真信號包含沖擊信息、正余弦信息和噪聲信息3種不同的成分，其中沖擊信息選取2個諧波頻率調(diào)制一個指數(shù)衰減的脈沖來仿真滾動軸承故障沖擊信號[9]，

x(k)=e-at[sin (2πf1kT)+sin (2πf2kT)]，

(1)

式中：t=mod(kT,1/fm)；a=800；fm=100 Hz；f1=3 kHz；f2=8 kHz；T=1/25 000 s；a,fm,f1,f2,T分別表示指數(shù)頻率、調(diào)制頻率、2個載波頻率和采樣間隔。當(dāng)加入正余弦和噪聲成分后，原始信號表達(dá)式為

x(k)=e-at[sin (2πf1kT)+sin(2πf2kT)+

A1cos(2πf3kT)+A2sin(2πf4kT)]+A3cos(2π·

f5kT)+A4rand(1,2 500)，

(2)

式中：f3=300 Hz；f4=500 Hz；f5=800 Hz；A1=2,A2=2.5,A3=3,A4=0.2。故障沖擊信號及混合信號如圖2和圖3所示。經(jīng)分析，最佳延遲和嵌入維數(shù)均為5。經(jīng)相空間重構(gòu)并進(jìn)行獨立分量分析，結(jié)果如圖4所示，不但周期性的沖擊信息(第1個分量)被明顯提取出來了，其他分量也得到了有效的分離。并且當(dāng)噪聲較小時，分離或沖擊特征提取效果會更加明顯。小波包分解雖然也能夠提取出沖擊信息， 卻不能實現(xiàn)信號分離。

圖2 沖擊信號

圖3 混合信號

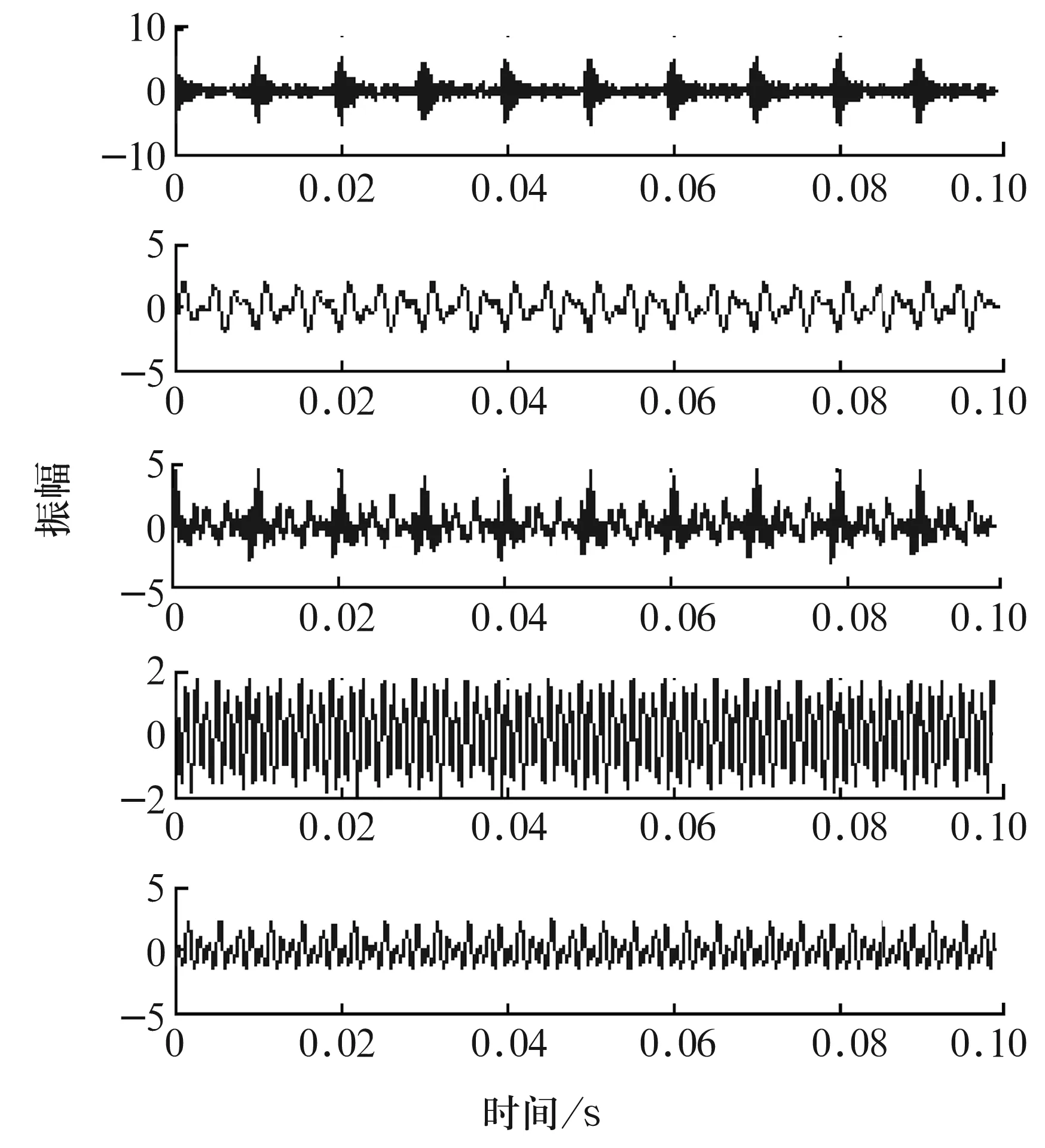
圖4 相空間-獨立分量分析

4 實例分析

4.1 試驗

軸承故障信號來自某石化廠低壓聚乙烯混煉機(jī)齒輪箱軸承座振動信息。根據(jù)對混煉機(jī)組的跟蹤監(jiān)測，某次所得到的軸承座振動信號較前幾個月連續(xù)測得信號RMS值明顯增大，據(jù)此猜測齒輪箱的軸承可能發(fā)生故障。振動信號采集選用加速度傳感器，設(shè)備結(jié)構(gòu)簡圖如圖5所示。軸承型號為NSK22338，采樣頻率為12 800 Hz，采樣長度為4 096，經(jīng)計算，軸承嚙合頻率為387.5 Hz，內(nèi)圈、外圈、保持架及滾動體的特征頻率分別為68.75，48.2,3.44和21.58 Hz。測量所得原始振動信號的時域信息如圖6所示。

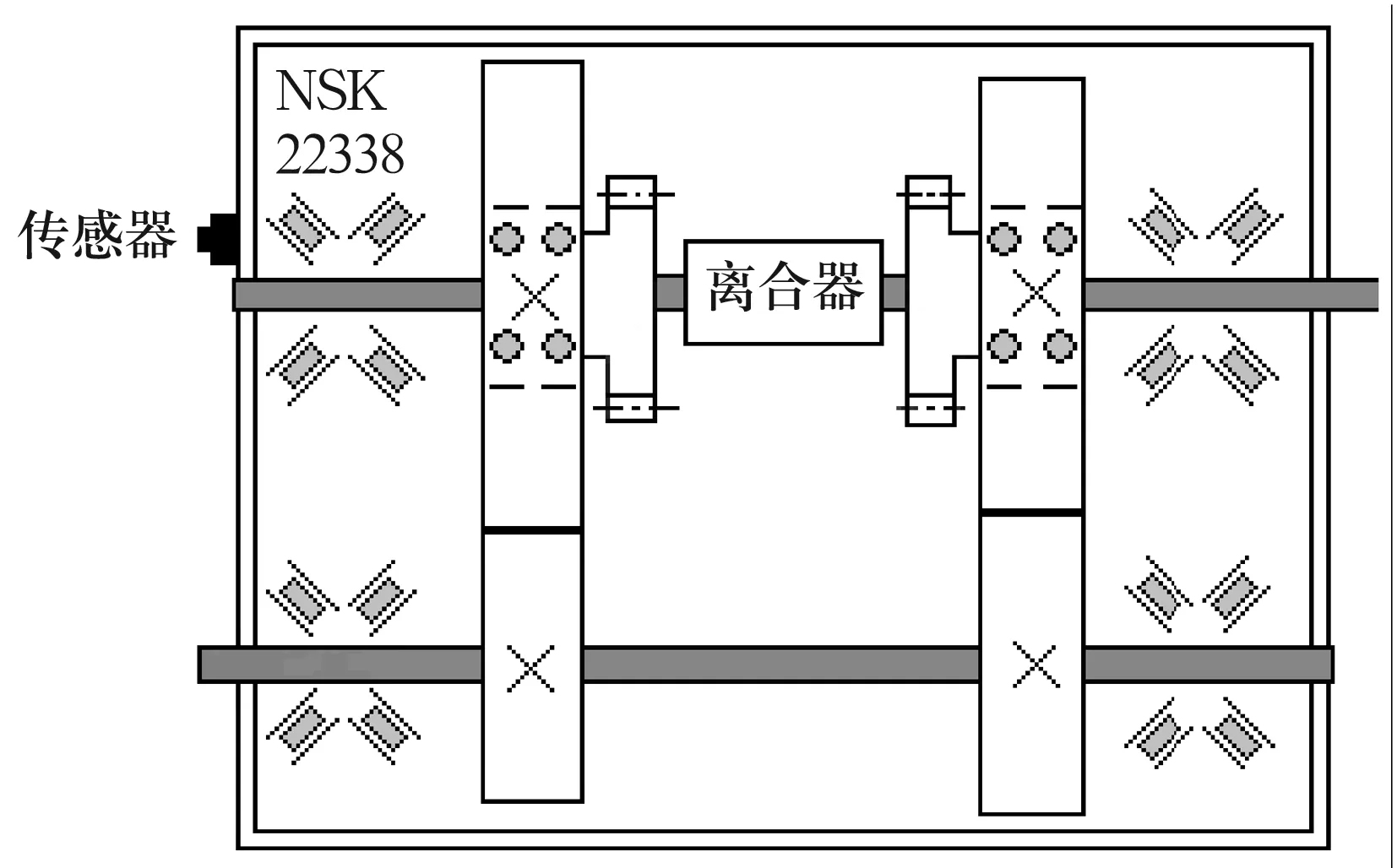
圖5 設(shè)備結(jié)構(gòu)示意圖

4.2 故障沖擊成分提取

觀察圖6可知，時域波形有沖擊但不明顯，僅從時域無法判定故障類型，故判斷該滾動軸承處于早期故障狀態(tài)。

圖6 原始信號

峭度是反映信號幅值分布特性的歸一化4階數(shù)值統(tǒng)計量，能夠反映概率密度曲線的陡峭程度，是衡量沖擊信息的有效參數(shù)之一，而沖擊信息是滾動軸承故障的典型代表。峭度隨信號類型不同而改變的特性使得在滾動軸承的實際故障診斷中，可以作為確定滾動軸承故障頻帶的參數(shù)之一[10]。經(jīng)相空間重構(gòu)并進(jìn)行ICA分離后，各獨立振源已被分離出來，ICA各分量的峭度分布如圖7所示。顯然，第5個分量的峭度值大于3，并明顯高于其他分量，包含了最多的故障沖擊信息，故將第5個分量作為特征分量進(jìn)行故障特征提取。

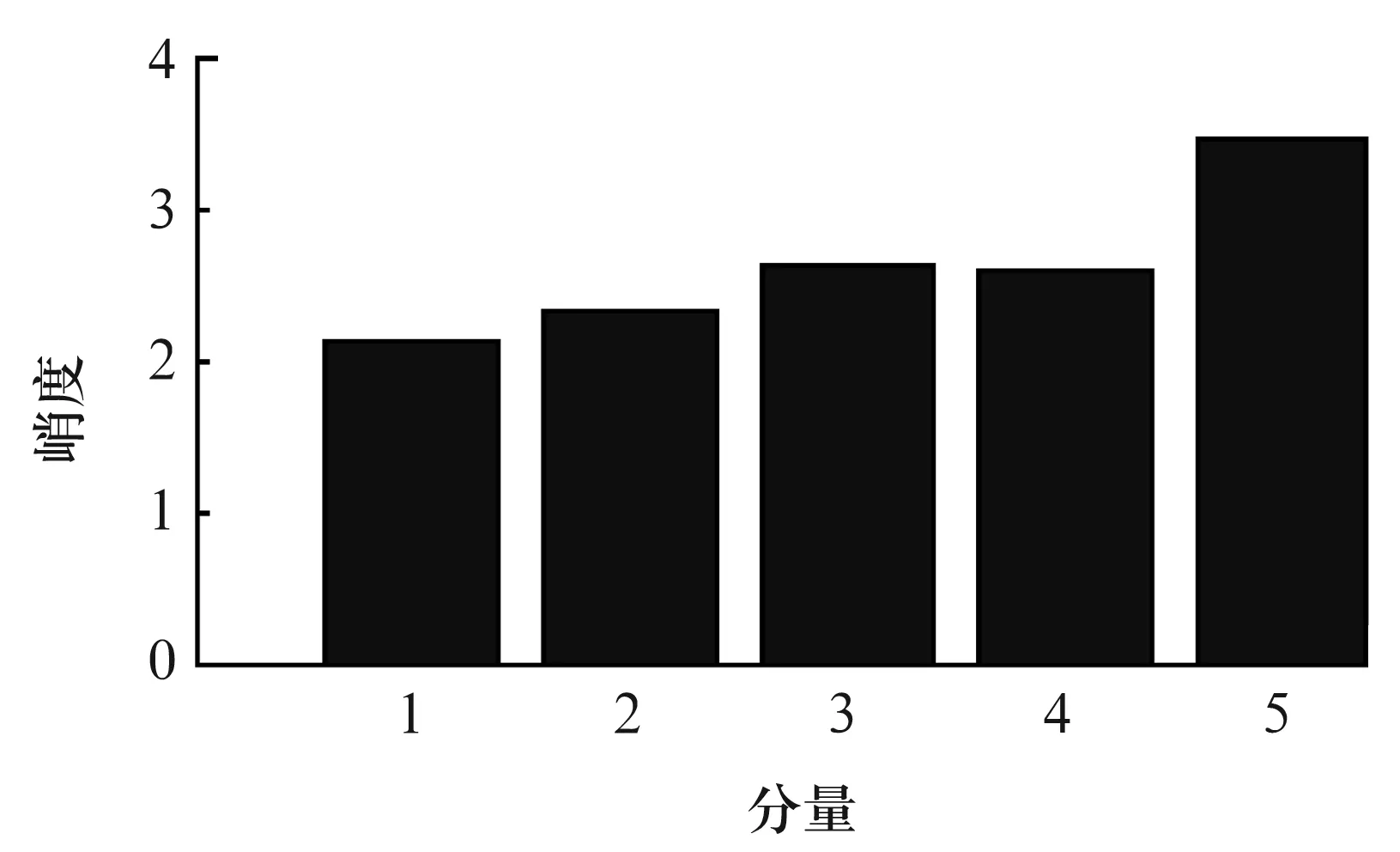
圖7 ICA分量峭度

分量5的時域圖形如圖8所示，對比圖6可知，經(jīng)過相空間-ICA時域提取后，其周期性的故障沖擊信息得到明顯改善。由于提取的特征頻帶中依然含有部分高頻噪聲干擾，為進(jìn)一步提純沖擊故障信息，對提取分量進(jìn)行3層小波分解，并選取低頻故障子帶，結(jié)果如圖9所示。經(jīng)小波降噪后，周期性故障信號得到進(jìn)一步改善，從圖中可以直接讀出故障沖擊周期T及其2倍周期2T，經(jīng)計算，T與滾動軸承內(nèi)圈故障特征周期完全吻合，所以判定該滾動軸承存在早期內(nèi)圈故障。

圖8 ICA分量5時域波形

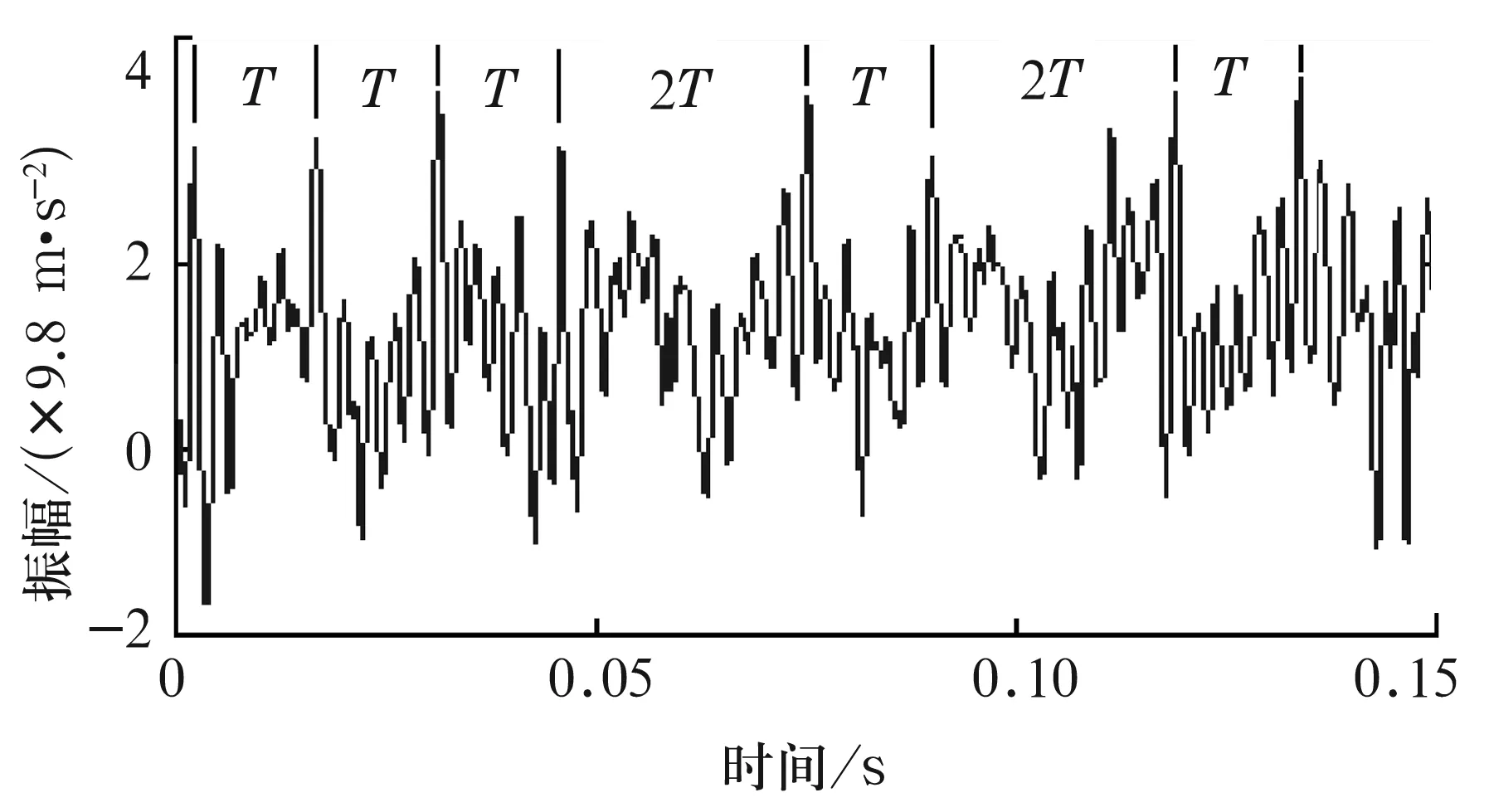
圖9 相空間-ICA時域波形

為了進(jìn)一步說明本方法的優(yōu)越性，采用傳統(tǒng)方法直接對原信號進(jìn)行3層小波包分解，依據(jù)峭度最大原則選擇故障特征頻帶。各頻段的峭度值分布如圖10所示，依據(jù)圖10判斷故障特征成分在第5個頻帶。將第5個頻段的小波包分解系數(shù)重構(gòu)并畫出其時域圖形，結(jié)果如圖11所示。對比圖8、圖9、圖11可知，采取相空間重構(gòu)的獨立分量分析方法，不管對提取的故障特征信息是否降噪(圖8未作降噪處理，圖9采取小波降噪)，其周期性的故障沖擊特征都要明顯優(yōu)于傳統(tǒng)的小波包-峭度特征提取方法(圖11)。因此，對于滾動軸承早期故障單通道特征提取，相比傳統(tǒng)的小波包-峭度特征提取方法，基于相空間ICA和小波降噪相結(jié)合的特征提取方法不但可行，且具有明顯優(yōu)勢。

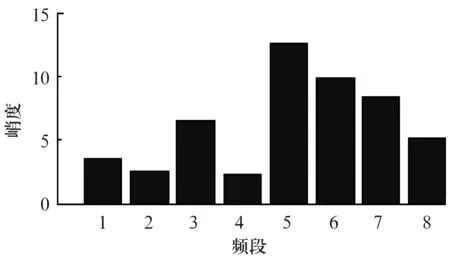
圖10 小波包頻帶峭度

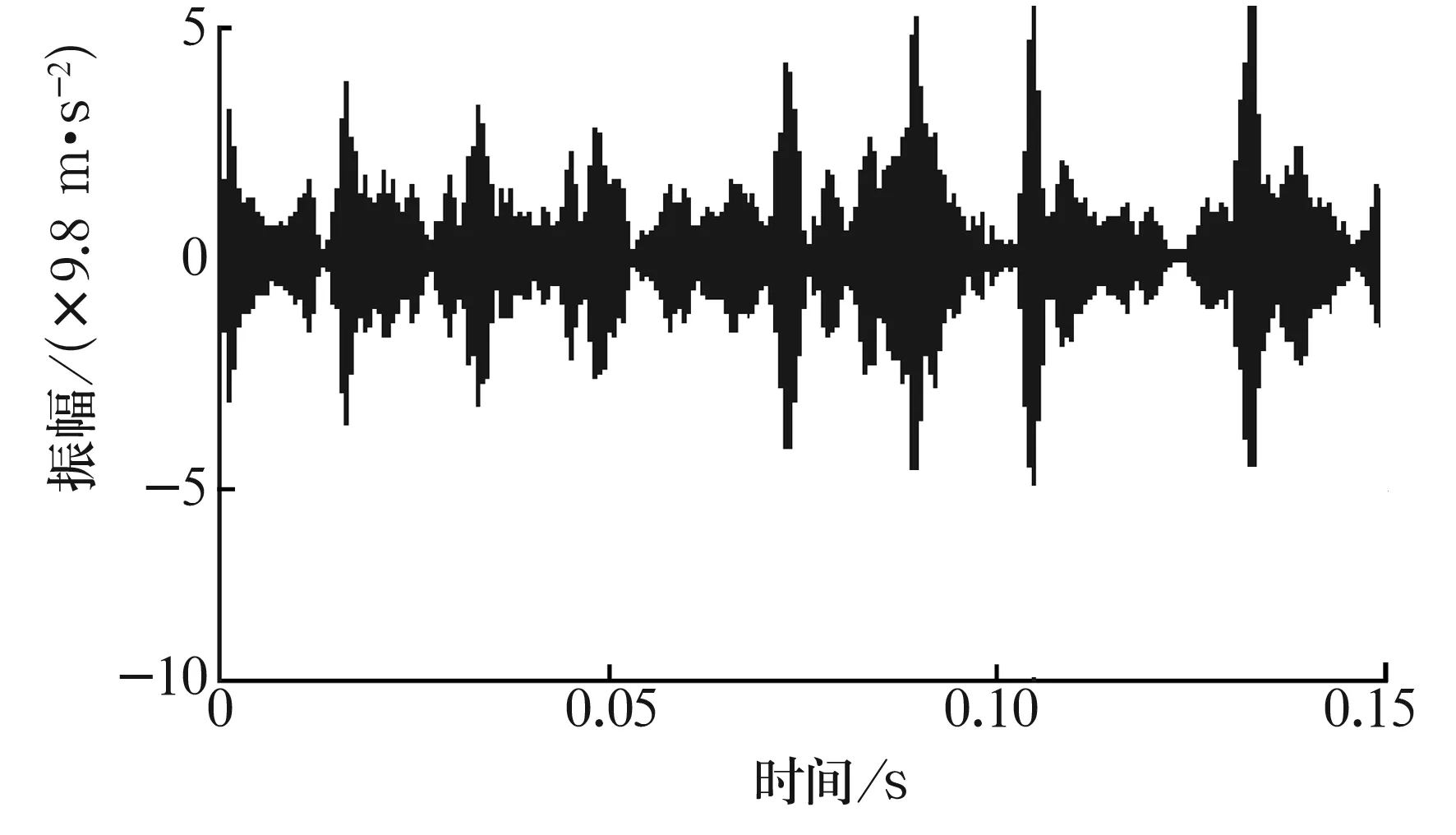
圖11 小波包-峭度時域波形

5 結(jié)束語

ICA是盲源分離中有效方法之一，然而對于單通道信號則無能為力，而基于相空間重構(gòu)的ICA信號分離方法，充分利用相空間能夠反映故障狀態(tài)下的動力學(xué)特性和ICA分離獨立信源的各自優(yōu)勢，巧妙地將二者結(jié)合起來。新的方法為滾動軸承采用單通道提取的故障特征信息不能進(jìn)行ICA提供了一種解決思路，而且從混有多振源和背景噪聲的滾動軸承振動信號中提取出故障沖擊成分，經(jīng)小波降噪，該故障沖擊特征更加明顯。基于相空間重構(gòu)的ICA信號分離方法實現(xiàn)了兩種理論的有機(jī)結(jié)合；先進(jìn)行時域故障沖擊特征提取，再進(jìn)行頻域降噪，實現(xiàn)了兩種診斷思路的結(jié)合，促進(jìn)了故障診斷技術(shù)的發(fā)展。