混沌理論在滾動軸承故障診斷中的應用

吳參，李興林，孫守遷，張燕遼，張仰平

(1. 杭州軸承試驗研究中心 博士后工作站，杭州 310022；2. 杭州電子科技大學 機械工程學院，杭州 310018；3.浙江大學 現代工業設計所，杭州 310027)

振動分析法是通過安裝在軸承座或箱體適當位置的振動傳感器監測軸承振動信號，并對此信號進行分析與處理來判斷軸承工況與故障的方法。由于滾動軸承早期故障振動信號容易湮沒在大量噪聲背景下，使得振動分析法的應用受到極大的制約。一般來說，振動烈度、峰值因子、偏態和峭度是判斷滾動軸承故障的常用特征值。但實際上，當軸承出現微弱故障時，其振動烈度不一定突然變大，很難在測量得到的振動信號中分辨提取出故障特征。近年來，一批國外學者采用了先進的信號處理方法和技術，以期達到更好的檢測效果[1-5]，但是仍沒有得到較好較穩定的效果。

混沌故障診斷是振動分析法中的一個重要分支。混沌是指確定性系統中出現的一種貌似無規則的、類似隨機的現象[6]。混沌系統對初始條件的敏感依賴，是系統內在的、固有的隨機性引起的，這是非線性系統在一定條件下表現出的特有現象。由于混沌系統對初始條件和參數的極度敏感，只要將被測的微弱信號加入到混沌系統中，就會導致該混沌系統的動力學行為發生本質的變化，應用這一特點可以檢測噪聲背景下的微弱信號。

1 軸承工作中的混沌振動

滾動軸承在工作過程中會產生大量的混沌振動。文獻[7]研究了游隙對滾動軸承振動形式的影響，提出了包含游隙的滾動軸承振動模型，分析了游隙大小和軸承轉動頻率對最大Lyapunov指數、Poincaré截面的影響。文獻[8]研究了空氣動力學影響下帶偏心力的四葉徑向軸承的振動情況，從功率譜密度圖以及分叉圖中可以發現大量的混沌現象。文獻[9]基于試驗研究了滾動軸承通向混沌的路徑，數據表明有分諧波道路和擬周期道路兩大類。

除了軸承本身以外，軸承座、軸、負載情況都會造成軸承的混沌振動。文獻[10]研究了齒輪負載下考慮動力學沖擊和摩擦的滾動軸承振動模型及其混沌振動情況。文獻[11-12]研究了軸承座的彈性阻尼對軸承混沌振動的影響。

由此，可以看到軸承的工作中包含了大量的混沌振動信號，軸承的混沌故障檢測是可行的。

2 混沌故障檢測

混沌故障檢測是由美國學者Birx在20世紀90年代首先提出的設想和設計[13]。而后國內、外眾多學者在混沌故障檢測上深入探索，并與其他信號處理方法交叉，取得了較理想的理論成果。在方法上，文獻[14-15]分別研究了基于混沌粒子群優化算法(CPSO)和支持向量機(SVM)的故障診斷算法。文獻[14]測試了沖擊、偏置、短路和漂移4種信號情況下的診斷結果，研究表明在大量試驗的基礎上該算法可以通過自學習得到較準確的診斷結果。文獻[15]對多故障并發狀態進行了檢測，結果表明在經過適當數據量的訓練后，該算法能夠較好地對并發故障進行分類。另外，文獻[16]提出了一種根據引入混沌振子系統中二維近似熵變化來判定故障模式的故障診斷方法。在應用上，文獻[17]將陣發混沌與滑窗符號序列結合，用于液壓泵的故障診斷，取得了良好的效果。此外，混沌故障診斷技術也被廣泛用于醫學信號分析，如文獻[18]研究了一種時空小波混沌方法應用于腦電波圖的老年癡呆癥診斷。

目前，對滾動軸承振動信號的檢測基本依賴于壓電式加速度傳感器，該類傳感器體積小，精度高，能夠滿足工業現場安裝的要求。其安裝方式一般如圖1所示，圖中2個壓電式加速度傳感器分別安裝在軸承座的12點和9點方向，測量軸承平面內垂直方向和水平方向的振動情況。在某些精度要求較高的場合，會安裝一個光學探針來測量滾動體的運動情況，從而更精確地估計軸承的故障頻率。

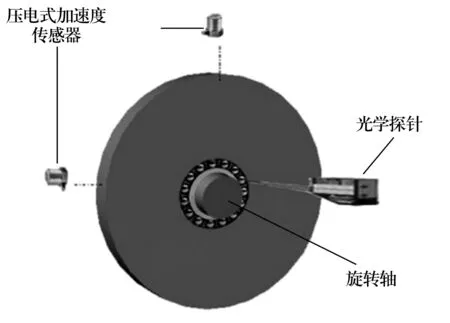
圖1 軸承檢測傳感器布置圖

3 混沌理論在軸承故障診斷中的應用

從現有文獻看，將混沌理論應用于滾動軸承故障診斷的方法主要有兩種：(1)引入混沌振子系統，通過臨界狀態的變化判定故障模式；(2)用混沌動力學方法提取特征值，標識各種故障模式。

3.1 混沌振子系統的應用

目前,混沌振子系統在滾動軸承故障振動檢測中的運用主要是混沌檢測模型相變的檢驗，即將混沌檢測模型參數調至閾值點，使系統處于一種臨界狀態，將待測微弱信號作為系統周期策動力的攝動，引入到檢測模型中，依據系統從混沌狀態到周期狀態發生的相變，檢測出微弱信號的存在。

國內眾多學者在利用混沌振子檢測微弱信號方面作出了重大貢獻。如文獻[19]用混沌振子檢測湮沒在高噪聲背景下的方波信號。文獻[20]提出了一種強噪聲背景下的頻率測量方法。此外，文獻[21]采用Melnikov方法作為混沌判據，利用混沌振子陣列實現對噪聲背景下微弱信號的檢測，并通過仿真試驗表明其檢測方法簡單、有效，檢測的精度也比較高。文獻[22]利用混沌振子檢測出淹沒在強噪聲背景中的微弱三角波信號。文獻[23]將混沌系統檢測弱信號方法與自相關方法和濾波方法相結合，得到了弱信號檢測的新方法(聯合檢測)。文獻[24]對淹沒在強分形噪聲中的信號進行多尺度小波變換，根據分形噪聲信號小波系數的平穩性，建立狀態方程和觀測方程，利用模糊自適應Kalman濾波和Duffing振子對噪聲的免疫力，來檢測微弱信號。

混沌檢測模型最常見的是Holmes型Duffing系統[25-27]，其方程為

(1)

式中：ω0為任意頻率；c為阻尼比；F0cos(ω0t)為Duffing系統內部周期驅動力。當加入被測周期信號和噪聲干擾后，(1)式變為

(2)

式中：ω1，θ分別為被測周期信號的頻率和相位；N為服從正態分布的隨機噪聲。如果將c固定，隨著F0的增大，該系統經歷了小尺度周期運動、分叉、混沌運動和大尺度周期運動4種狀態。一般選擇混沌運動和大尺度周期運動的臨界點作為檢測點，具體方法如下。

(1)將Duffing系統內部驅動頻率ω0設為被測信號頻率ω1，即ω0=ω1。ω1取值為軸承內圈、滾動體或外圈故障頻率等軸承故障特征頻率。

(2)應用Melnikov方法等計算系統從混沌運動到大尺度周期運動的臨界點Fd值。

(3)將F0設為略小于臨界點Fd。此時，若被測信號輸入為0，則系統處于混沌運動狀態。當被測信號輸入不為0，只要F0+F1>Fd，該系統就會由混沌運動轉變為大尺度周期運動。根據系統運動狀態的改變，監測信號中是否含有頻率為ω1的軸承故障信號。

但是這種運用混沌振子系統的方法對于不同的檢測對象有其適用的前提條件：(1)由于需要預先確定ω0，ω1的值，因此在檢測前軸承可能的故障頻率(即被測周期信號頻率)必須是已知的。而在實際情況中，該信號頻率只能通過動力學理論公式大致計算得到，其值并不精確。同時，對于不同的檢測對象要調整不同的診斷系統參數，需要“一機一調”，給工程實際應用帶來較大不便。(2)通過動力學理論公式計算得到的軸承故障頻率應貼近實際故障頻率，并在其鄰域內不存在其他周期成分，否則會影響診斷結果。而實際工程中由于外部噪聲原因可能引入周期信號，比如電網波動周期信號，在實際工程應用上存在不可避免的缺陷。

3.2 混沌動力學分析的應用

混沌動力學分析是將被測數據賦值給一個單變量時間序列{xn}，對該時間序列進行相空間重構，提取該序列的混沌特征量。由于混沌特征量是混沌動力系統最根本的幾何不變量，因此只有當軸承發生故障時，即該混沌動力系統發生變化，其混沌特征量才會隨之發生變化。其基本思想是：任意混沌系統在經過初始的收斂過程后，會產生一種規則的軌跡，即混沌吸引子。由于系統中的任意變量都是與其他的變量相互作用，相互影響的。因此，所有這些相關變量的信息都包含在一個變量的變化過程當中。所以，可以通過觀察足夠長度的某一變量的變化，從該時間序列中提取和再現原有系統的動力學規律[6]。

對被測數據作以下相空間重構

(3)

從而形成m維狀態空間，在重構的m維狀態空間中可以建立數學模型

xn+1=G(xn)。

(4)

形成m維空間，只要m≥2d+1，動力系統的幾何結構就能完全打開，其中d為系統中吸引子的維數，τ為時間延遲間隔。由于狀態空間Rm中的吸引子的幾何特征與原動力系統的幾何特征完全等價，所以原動力系統的任意微分或拓撲不變量可以在重構的狀態空間中計算。

目前，在故障診斷中常用的混沌特征值主要有最大Lyapunov指數、關聯維數和Kolmogorov熵等。

3.2.1 最大Lyapunov指數

從時間序列中計算最大Lyapunov指數的最早工作是軌線法。文獻[28]提出了小數據量法求最大Lyapunov指數的方法，該方法在相空間重構后，其基本步驟如下：

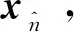
(5)

(2)對相空間中每個點xn，計算出該一對鄰點的i個離散時間步后的距離dn(i)為

(6)

(3)對每個i，求出所有n的lndn(i)平均y(i)，即

(7)

q為非零dn(i)的數目，并用最小二乘法作出回歸直線，該直線的斜率就是最大Lyapunov指數。

3.2.2 關聯維數

關聯維數是分形維數的一種，能定量地描述混沌吸引子的分形特征，由于計算方便，在軸承故障診斷中應用較為廣泛。在相空間重構后，其基本步驟如下：

(1)計算相空間各向量間的距離

rij=|Yi-Yj|；

(8)

(2)在min(rij)和max(rij)間取一適當的r，計算得

(9)

式中：C(r)為距離小于r的向量對在所有向量對中所占的比例；r為吸引子自相似結構的無標度區；H(x)為

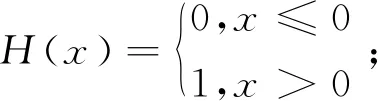
(10)

(3)計算關聯維數

(11)

3.2.3 Kolmogovov熵

Kolmogorov熵定義為信息的平均損失率，但在不知系統動力學方程時，Kolmogorov熵難以計算得到。由于K2≤K1≤K0,其中K2為Renyi熵，K1為Kolmogorov熵，K0為拓撲熵。因此通常計算K2熵作為Kolmogorov熵的近似。其計算方法與關聯維數的步驟(1)，(2)相同，而后計算

(12)

混沌動力學分析方法目前已經引起眾多學者的關注，但是也存在著不可回避的問題：(1)混沌動力學方法在時間序列賦值前一般需要進行濾波，該濾波頻率及方法與后續混沌動力學分析之間的關系缺少理論指導，目前的文獻中該濾波一般憑研究人員經驗自行決定。(2)混沌特征量包含眾多參數形式，如何選擇及選擇多少個混沌特征量都是懸而未決的問題。

4 結束語

到目前為止，對于混沌理論在滾動軸承故障診斷中的應用，國內還主要停留在理論研究或實驗室階段，在市場上還沒有以混沌理論為基礎的的滾動軸承故障診斷設備問世。混沌理論在滾動軸承故障診斷中的應用在以下方面有待進一步研究。

(1)混沌理論的應用能夠通過檢測故障特征判定滾動軸承故障。但是相同的特征量變化對于不同的滾動軸承可能意味著不同的故障模式，因此需要明確故障模式與混沌故障特征的映射關系。

(2)目前混沌理論在故障診斷中的應用基本都是對單一故障提出的，而實際工程應用中，故障模式往往是并發甚至是多發的，因此在并發或者多發情況下混沌故障特征的變化能否滿足故障識別的要求還要進一步探索。

(3)混沌理論的應用主要起到了滾動軸承故障特征提取的作用，仍需要進行診斷決策算法的研究。