角接觸球軸承的應力場與相對疲勞壽命分析

程超，汪久根，王愛林，洪玉芳

(浙江大學 機械工程學系，杭州 310027)

角接觸球軸承廣泛應用于機床主軸和汽車輪轂單元中，要求有高的耐磨性和較長的疲勞壽命。然而，軸承的耐磨性和疲勞壽命都與鋼球與內、外溝道的應力場密切相關。軸承的疲勞裂紋源有表面粗糙峰微小裂紋和零件表層的疲勞導致的裂紋[1]，可以通過表面精加工減少或消除；但是在一定應力循環次數后，由于零件表層材料受交變應力作用，會在表層產生裂紋，裂紋擴展后形成疲勞剝落。因此，零件表層應力場的研究就成為長期以來關注的問題[2]。

角接觸球軸承的接觸問題為橢圓接觸。文獻[3]提出了橢圓參數和最大正交剪應力的簡易計算方法。文獻[4]認為接觸角隨鋼球位置角和徑向載荷變化。文獻[5]提出了用Excel編程計算橢圓接觸問題的方法，得到了接觸應力，橢圓長、短半軸和彈性趨近量。文獻[6]給出了橢圓參數計算的擬合公式，但在主曲率相等時誤差較大。文獻[7]認為，細化網格和增大計算區域可以提高接觸問題的計算精度。文獻[8]給出了橢圓接觸區方向角的計算公式，用于求解一般橢圓接觸問題。文獻[9]計入球組壽命，計算了整套深溝球軸承和角接觸球軸承的疲勞壽命，并分析了密合度對軸承疲勞壽命的影響。文獻[10]分析了真空處理軸承鋼的應力壽命指數。文獻[2-7]對接觸應力的分析已經十分詳細，然而軸承的疲勞壽命與應力場之間關系的分析仍沿用Hertz理論，這方面有待進一步的詳細分析。另一方面，軸承零件的加工誤差對軸承壽命的影響也有待研究。

軸承的球徑誤差和接觸角、溝道曲率半徑等幾何參數對接觸應力場有影響，文中擬研究角接觸球軸承的Mises應力場，分析球徑變化、溝曲率半徑系數和接觸角對接觸應力場的影響，進而得到其對滾動軸承疲勞壽命的影響。

1 彈性接觸的計算模型

將鋼球與溝道作為兩個彈性體，施加徑向載荷Fr后產生彈性變形，形成橢圓接觸區域Ω。定義δ為兩個彈性體之間產生的彈性趨近量，則

ω1+ω2+f1+f2=δ，

(1)

式中：ω1,ω2分別為鋼球和溝道在接觸點產生的彈性變形；f1,f2分別為鋼球和溝道表面在加載載荷前距名義接觸點切線的垂直距離。ω1,ω2可由彈性力學中的Boussinesg公式求得

(2)

式中：E1,E2分別為鋼球和套圈的彈性模量；ν1,ν2分別為鋼球和套圈的泊松比；s,t為接觸區域Ω中點的坐標；p(s,t)為徑向載荷作用下分布在接觸區域Ω上的接觸應力。

同時，根據平衡條件，表面應力分布沿接觸區域的積分應與所作用的總載荷相等，即

(3)

(1)～(3)式組成了角接觸球軸承鋼球與溝道接觸問題的基本方程。計算中將接觸區域劃分為多個單元，在每個單元格上假定接觸應力為定值，然后將(1)、(3)式離散成一個線性方程組，通過求解方程組求得每個單元格上的接觸應力。

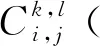
(4)

鋼球與溝道在接觸點的彈性變形經離散化后可以寫為

(5)

軸承的接觸疲勞是裂紋發生和擴展的結果。裂紋可能先從表面下某一深度產生，繼而擴展到表面，裂紋的產生和擴展，除了與物體表面或內部的材料缺陷有關外，主要受零件表層內的應力分布影響。要分析角接觸球軸承的疲勞機理和壽命，就需要分析接觸表面下的Mises應力場。在上述計算獲得接觸應力p(s,t)，并取鋼球與溝道的摩擦因數為0.08后，可得到切向摩擦力F(s,t)分布，然后用文獻[11]的方法計算出零件表層的Mises應力場。軸承的疲勞壽命與其內、外溝道和鋼球的壽命存在以下關系[9]

(6)

式中：Lir，Ler分別為內、外溝道的疲勞壽命；e為系數，對于點接觸，e=10/9。

接觸表面下平行于滾動方向的最大Mises應力決定疲勞裂紋的發生，應力循環次數越大和受應力體積越小，則材料疲勞破壞的概率越大。Ioannides和Harris疲勞壽命計算模型可表示為[12]

(7)

式中：σM為最大Mises應力；z0為最大Mises應力所在深度；N為應力循環次數，以百萬次計；V為受應力體積；c，h為待定指數，對于點接觸，c=31/3，h=7/3。應力循環次數可表示為

N∝uL，

(8)

式中：u為軸承轉動一周的應力循環次數；L為以百萬轉為單位的壽命。在獲得接觸表面下的Mises應力分布后，可根據(6)～(8)式計算出軸承的相對疲勞壽命。

2 分析結果

這里采用的為7010C角接觸球軸承，材料為GCr15鋼，軸承具體參數為：外徑D=80 mm；內徑d=50 mm；球組節圓直徑Dpw=65 mm；球徑Dw=8.73 mm；接觸角α0=15°；內溝道曲率半徑系數fi=0.52；外溝道曲率半徑系數fe=0.52。取鋼球與溝道的接觸載荷F=200 N，并設定軸承內圈旋轉，外圈固定。根據以上參數計算得到的鋼球與內、外溝道的接觸應力分布呈半橢球體狀，接觸應力的最大值p0=1.348 GPa。

計算得到的零件表層Mises應力分布如圖1和圖2所示。沿軸承周向上，最大Mises應力為0.413 GPa，約為0.31p0，距接觸表面的深度為79.7 μm，此處即為疲勞裂紋的擴展源。在摩擦力的作用下，接觸區內的最大Mises應力位置偏離接觸中心線，如圖2所示。

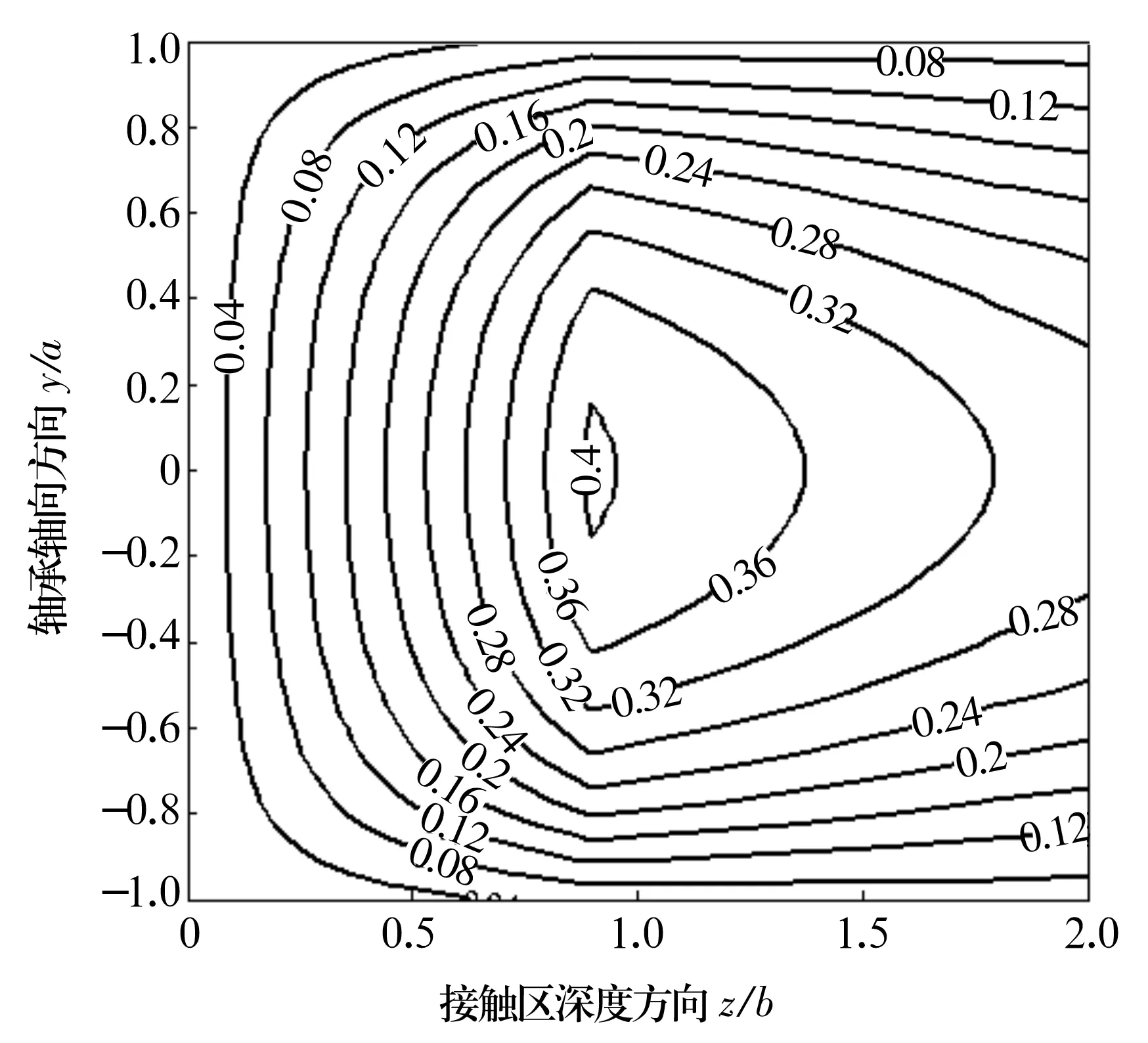
圖1 沿軸承軸向的Mises應力場

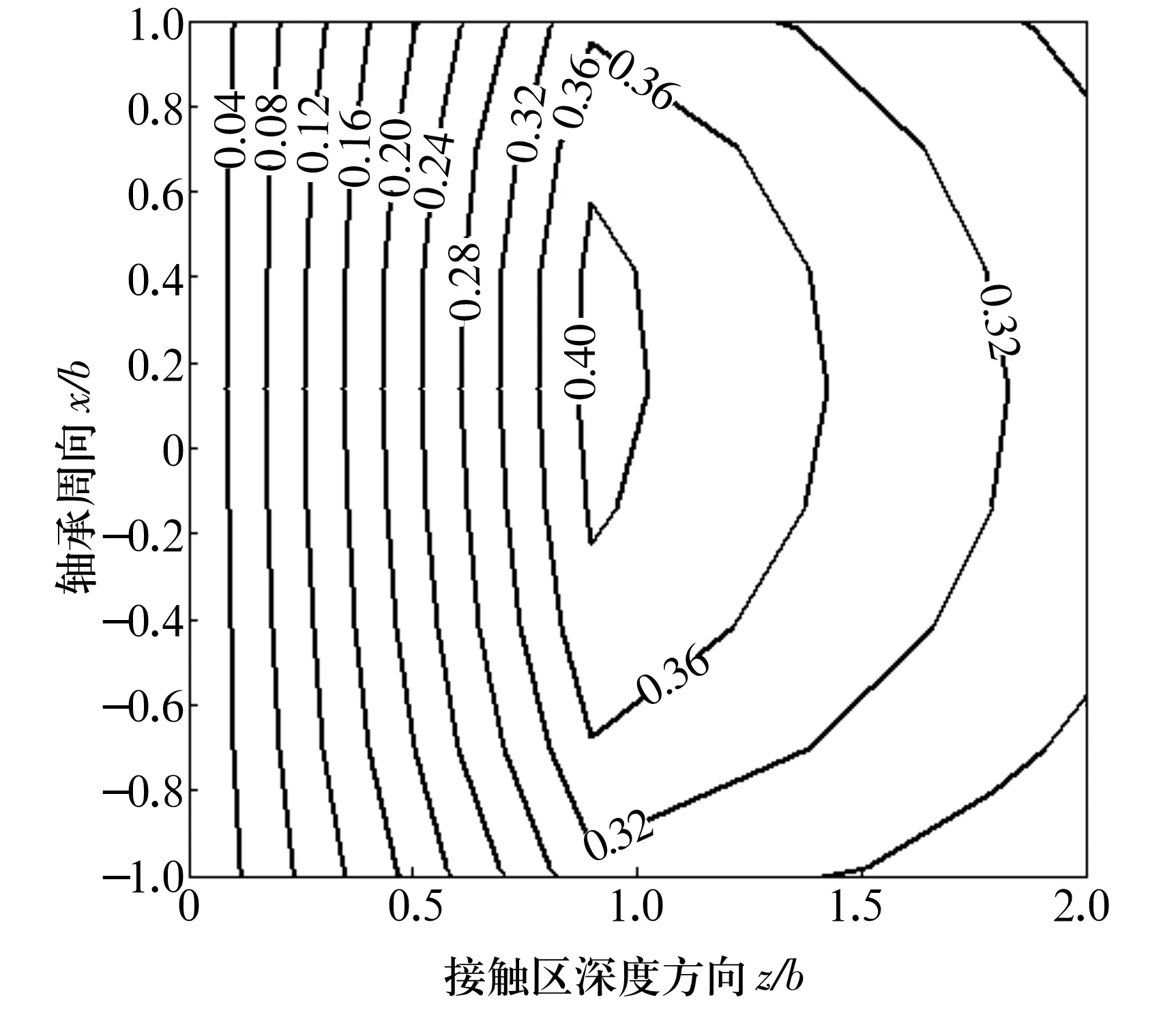
圖2 沿軸承周向的Mises應力場

2.1 球徑變化的影響

鋼球制造過程中，每批鋼球之間的直徑存在變化。鋼球直徑的改變對Mises應力會產生影響。取鋼球直徑變化范圍為-1%～1%，其他參數不變，計算Mises應力，結果如圖3所示。從圖中可以看出，隨著鋼球直徑的增大，最大Mises應力值減小，而最大Mises應力值所處的深度值增大；在軸承周向平面內的最大Mises應力值始終大于軸向平面內的值，說明疲勞首先發生在軸承周向上。鋼球直徑變化會對接觸橢圓面積的大小產生影響，也會使接觸應力分布發生變化，這些都會影響到最大Mises應力的深度值。以公稱球徑的壽命為基準進行對比，結果如圖4所示。從圖4中可以看出，軸承疲勞壽命隨著鋼球直徑的增大而提高。

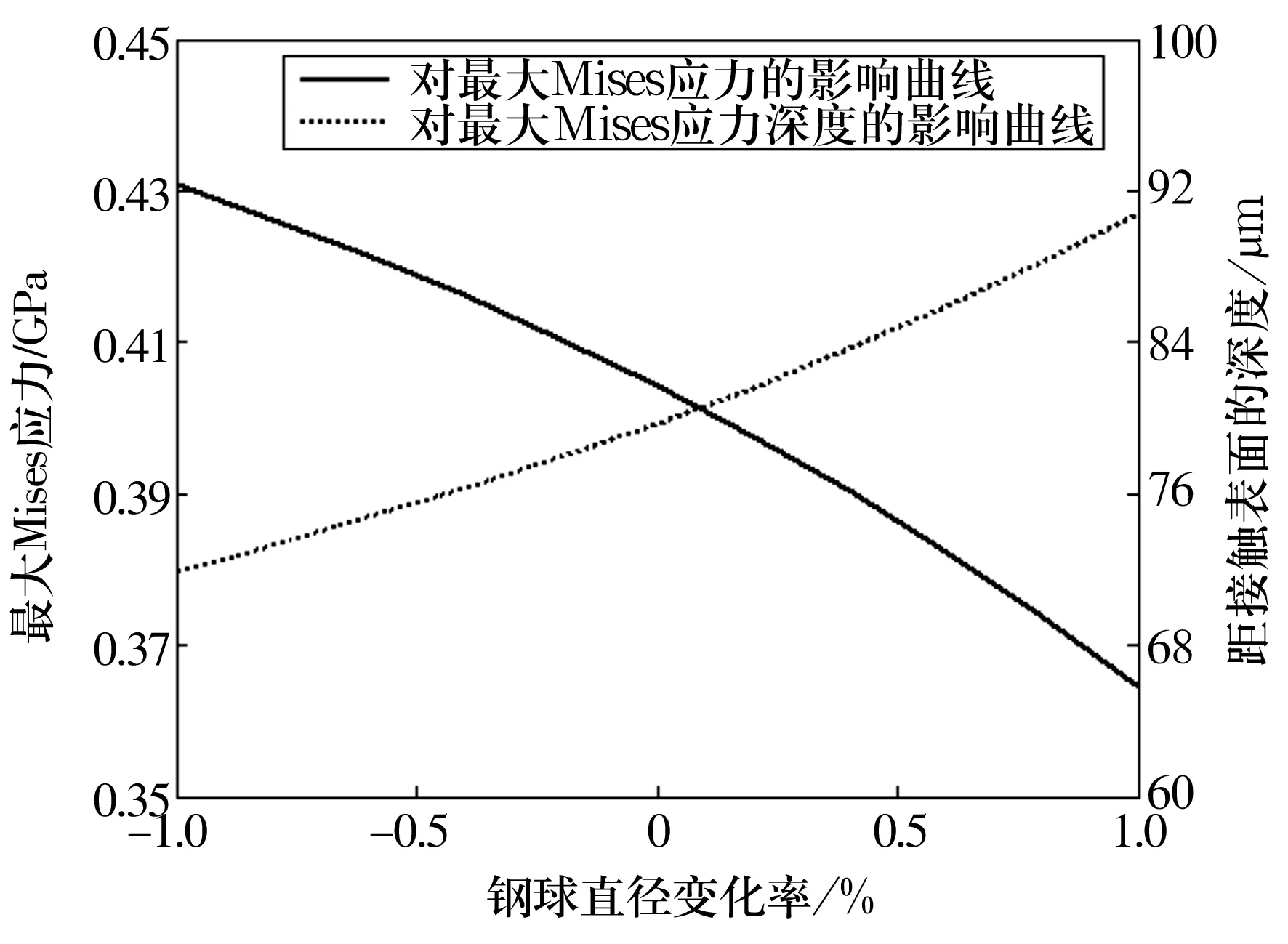
圖3 球徑變化對Mises應力的影響

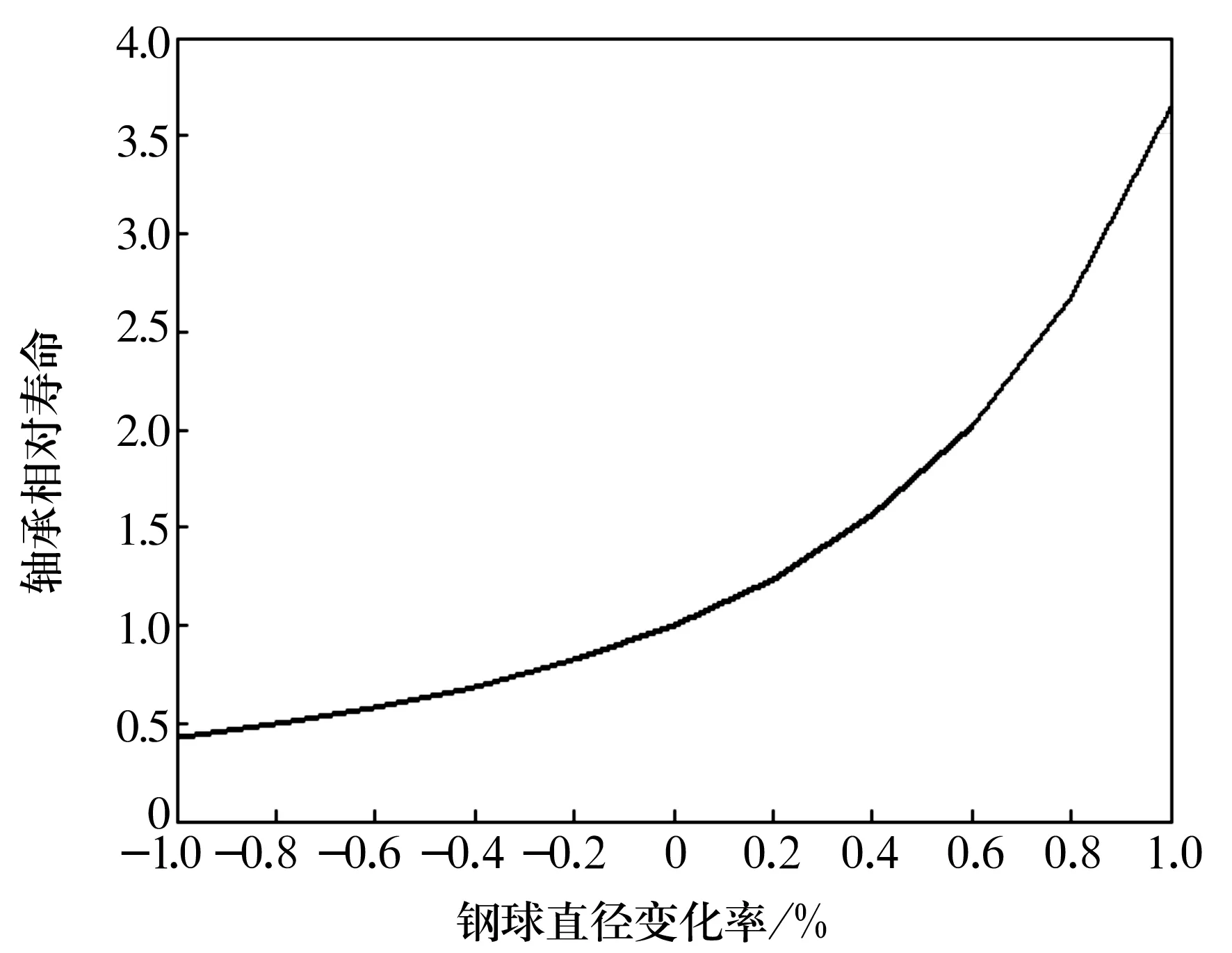
圖4 球徑變化對軸承疲勞壽命的影響

2.2 溝曲率半徑系數的影響

考慮內溝道曲率半徑系數fi的影響時，設定外溝道曲率半徑系數fe=0.520，fi的變化范圍為0.510～0.530，如圖5所示。考慮fe的影響時，設定fi=0.520，fe的變化范圍為0.510～0.530，如圖6所示。最大Mises應力隨溝曲率半徑系數的增大而增大；而其深度值卻隨溝曲率半徑系數的增大而減小，即疲勞擴展源的深度變小。

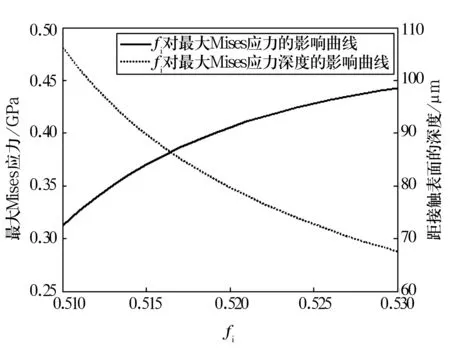
圖5 軸承周向上fi的影響曲線

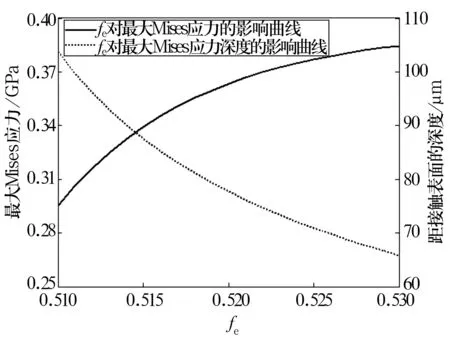
圖6 軸承周向上fe的影響曲線

同樣的，以軸承周向上的最大Mises應力進行壽命計算，并與內、外溝曲率半徑系數為0.52時的壽命進行對比，如圖7所示。從圖中可以看出，軸承疲勞壽命隨著溝曲率半徑系數的增大而減小，且內溝道曲率半徑系數fi對軸承疲勞壽命的影響比外溝道曲率半徑系數fe的影響要顯著得多。

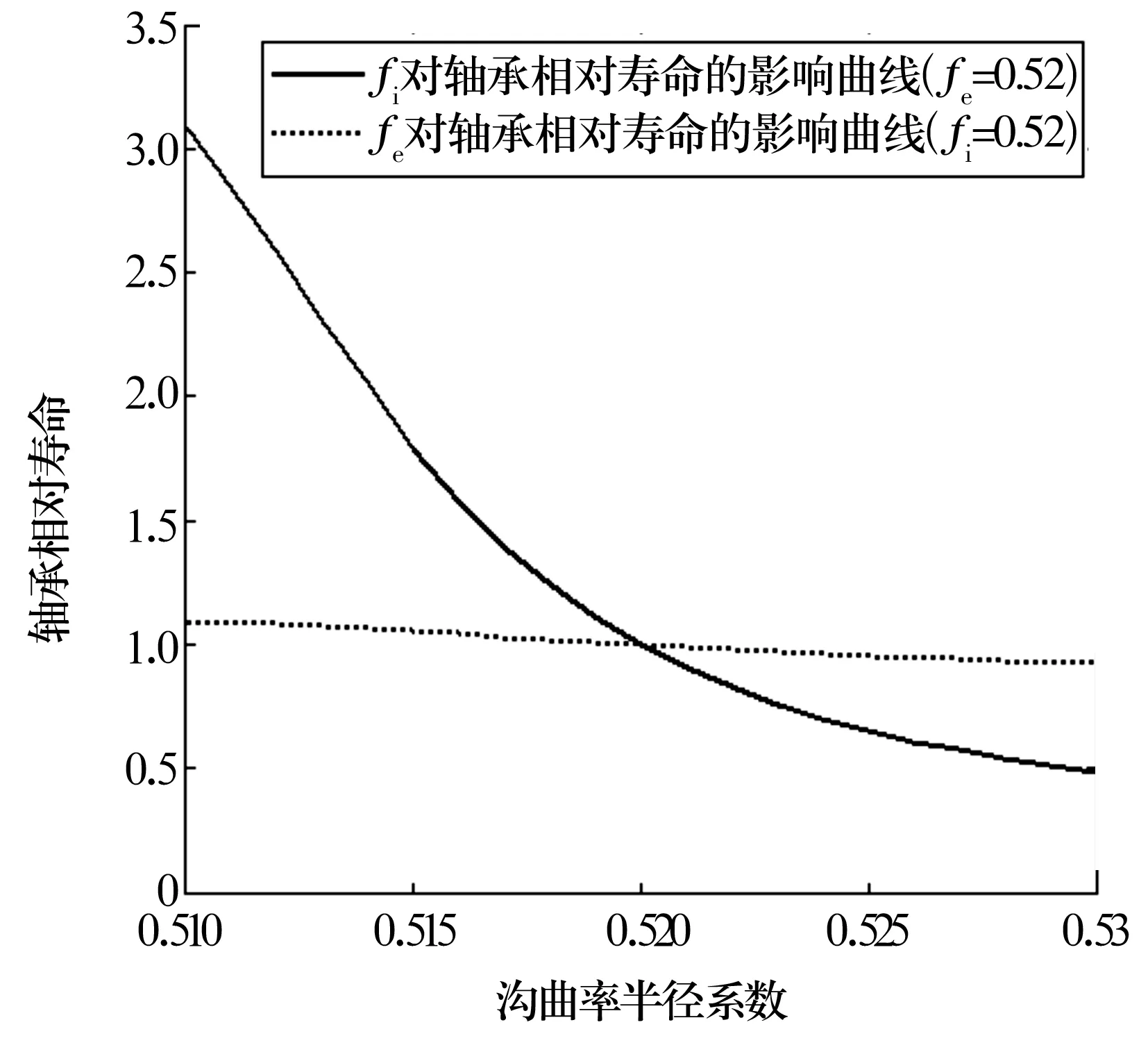
圖7 溝曲率半徑系數對軸承疲勞壽命的影響曲線

2.3 徑向游隙的影響

選取0組(標準組)、1組和2組徑向游隙，分析其對最大Mises應力及軸承壽命的影響，結果如圖8～圖10所示。由圖可知，最大Mises應力隨徑向游隙的增大而減小，其深度值在徑向游隙增大時基本保持不變。徑向游隙對軸承壽命的影響曲線如圖11所示。從圖11可以看出，軸承疲勞壽命隨徑向游隙的增大而減小，但受徑向游隙的影響較小。

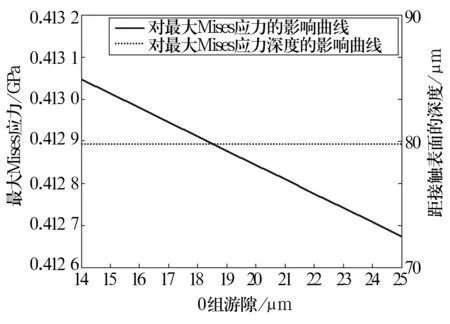
圖8 0組游隙的影響曲線

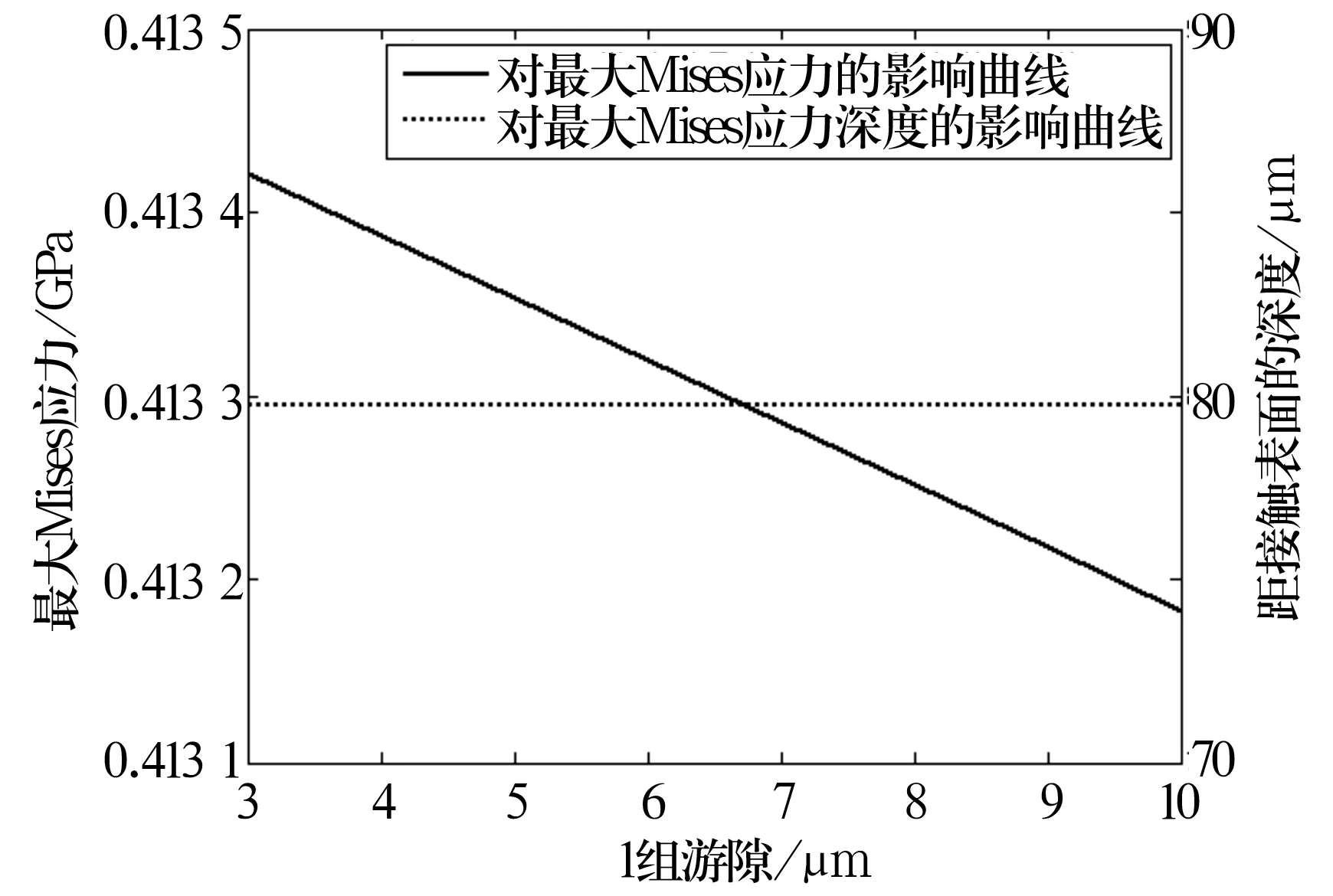
圖9 1組游隙的影響曲線

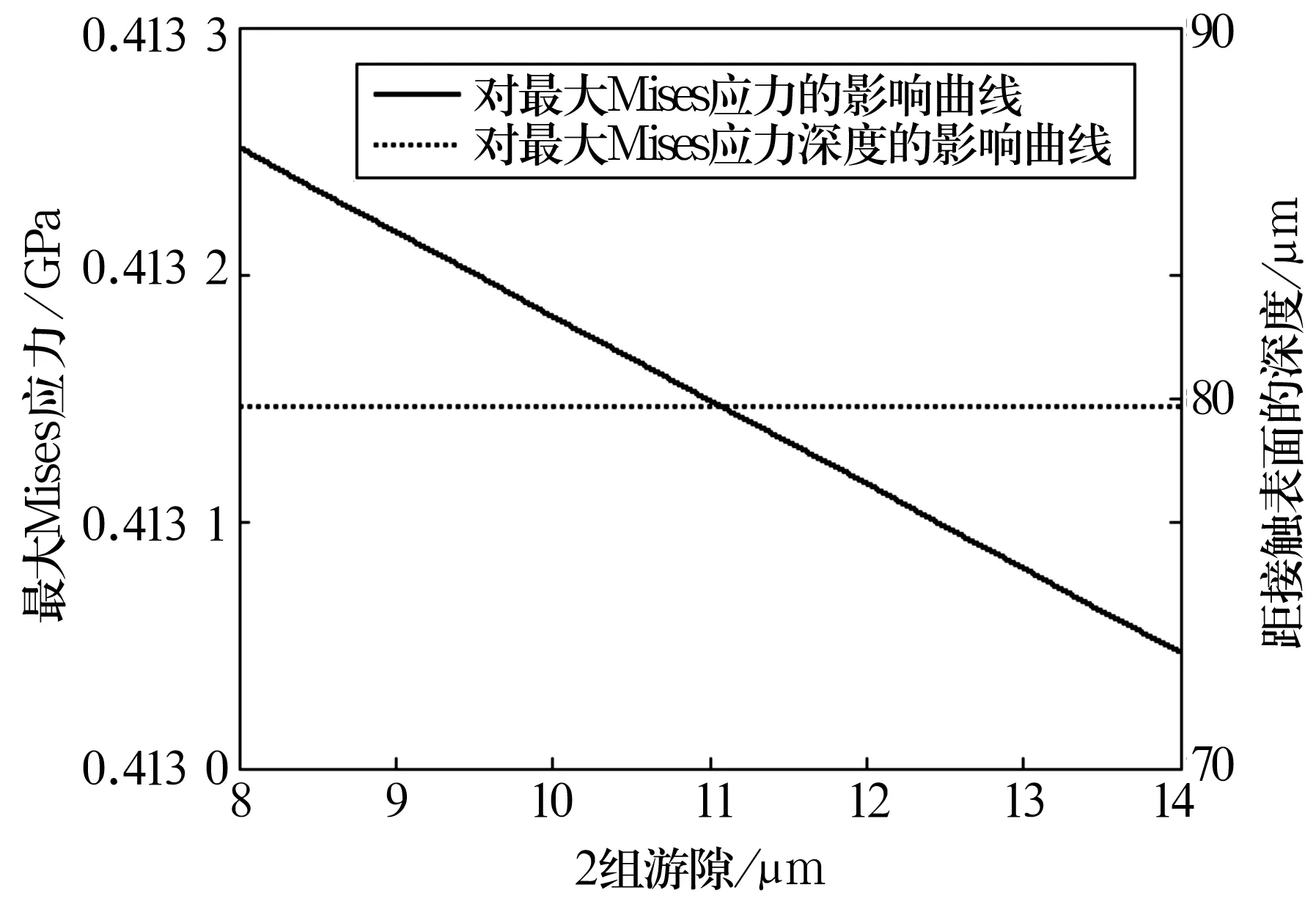
圖10 2組游隙的影響曲線

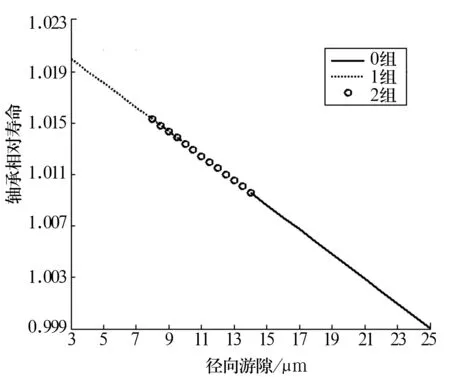
圖11 徑向游隙對軸承壽命的影響曲線

3 結論

(1)零件表層內Mises應力的最大值總是出現在軸承周向上，即表層疲勞源出現在軸承周向中間面內。

(2)軸承疲勞壽命隨著球徑的增大而增大，隨溝曲率半徑系數和徑向游隙的增大而減小。

(3)球徑、溝曲率半徑系數和徑向游隙對軸承疲勞壽命的影響程度是不相同的；內溝道曲率半徑系數和球徑的變化對軸承疲勞壽命影響較大，而外溝道曲率半徑系數和徑向游隙對軸承疲勞壽命的影響較小。