等速萬向節滑移曲線模糊測量法

劉曉軍 ，時輪，秦緒起

(1.上海交通大學 機械與動力工程學院，上海 200240；2.上海三一科技有限公司，上海 200000)

按照性能，等速萬向節分為定心型和軸向滑移型兩大類，一個等速萬向節傳動系統一般由定心型等速萬向節、軸向滑移型等速萬向節和傳動軸組成，其中定心型萬向節安裝于車輪一側，軸向滑移型萬向節安裝于差速器一側，中間的傳動軸用于萬向節連接，起傳遞運動的作用。滑移型等速萬向節性能測試是整個等速萬向節總成綜合性能測試項目中至關重要的一項。

根據等速萬向節總成標準JB/T 10189—2000[1]的規定，滑移型等速萬向節的性能參數主要取決于許用工作角度和伸縮滑移量。許用工作角度能夠保證滑移端在許可角度范圍內靈活擺動，從而適應各種惡劣工作環境對擺動角度的要求。

而伸縮滑移量能夠保證滑移端在許可位移范圍內自適應地調整軸向間距，降低惡劣工況下導致的振動和沖擊。這2項性能參數皆通過滑移與擺角特性曲線體現，因此該曲線基本可以作為滑移型等速萬向節合格與否的評價指標。如果實際測量曲線能夠將理論曲線完全包絡，則表明該滑移型萬向節合格;反之若理論曲線超出實際測量曲線，則表明該萬向節未達到設計要求。

目前滑移曲線的傳統測量法采用等間距測量，減小間距將導致試驗效率降低，若提高效率則不能準確識別滑移曲線發生轉折的區域，丟失重要的曲線特征信息，從而難以準確代表真實滑移曲線。在此，提出了滑移曲線的模糊測量算法，能夠準確識別曲線的直線區域和發生轉折的區域，并在不同區域分配適當的測量點數，可更加準確、高效地逼近真實曲線。

1 等速萬向節滑移曲線測量

1.1 傳統測量法

目前采用的等速萬向節滑移曲線測量法是從滑移端壓縮量最大處開始，將萬向節等間距拉伸一定長度，并測量該位移處的許用工作角度，直到拉伸至最大拉伸處為止，然后將許用工作角度按照位移量繪制成滑移擺角曲線[2]。

傳統滑移曲線測量法簡易方便，能在一定程度上滿足測量要求。若需提高測量效率，滿足生產要求，只能減少測量點數，這樣會損失大量的曲線信息，特別是滑移曲線發生轉折的區域，影響對工件性能的正確評價；而如果測量點數太多，固然能更準確地逼近真實的滑移曲線，但會延長測試時間，降低測量效率和測試臺的使用壽命。

1.2 基于模糊算法的測量法

1.2.1 測量思路

由于滑移型萬向節特定的內部結構，其理論滑移曲線為分段連續折線段，如圖1所示[3]。由于測量誤差和萬向節的制造、裝配誤差，實際測量曲線的直線段部分只是近似的直線，而轉折點附近的區域則是一條不規則的弧線，并沒有明顯的直線轉折，如圖2所示。因此最佳的測量法應該能識別出轉折區域，并合理分配測量點，即在信息量較少的直線段分配較少的測量點，在信息量豐富的弧線段分配較多的測量點。

1.2.2 二次測量法

基于上述思想，采用了二次測量法：首先，按較大的給定位移間隔(根據測量速度要求而定)測量整個行程的許用工作角度；然后，通過模糊算法確定轉折區并分配最佳插入測量點數，從而得到二次測量位移值，并在返回行程中測量這些位移處的許用工作角度；最后，將2次測量結果合并得到最終測量結果。

1.2.3 最佳插入點數計算法

根據第1次測量的結果計算每一段折線的傾角，如果相鄰兩段折線的傾角未發生改變，則表明它們在一條直線上，如果后一段傾角相對前一段有所改變，則表明在后一段折線的某部分發生了轉折，因此需要增加測量點，以測得過渡弧線段的曲線特征。

但測量試驗中的測量誤差等因素會導致本應在一條直線上的相鄰兩段折線的傾角并不相同，從而引起誤判。另外，只能根據經驗確定過渡弧線段應增加的測量點數，后一段相對前一段的傾角越大，中間的過渡弧線的弧度或弧線范圍越大，即該區域包含的曲線信息越多，因此增加的測量點數也應該越多；反之亦然。同時，第1次測量時的固定位移間隔也很難確定，取值過大會降低測量精度，過小則會降低測量效率。

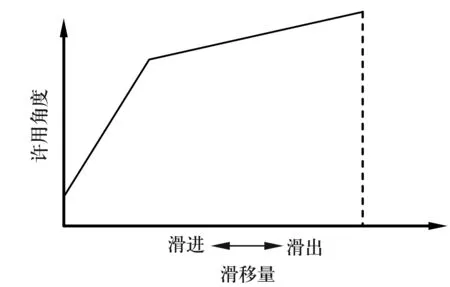
圖1 理論滑移曲線

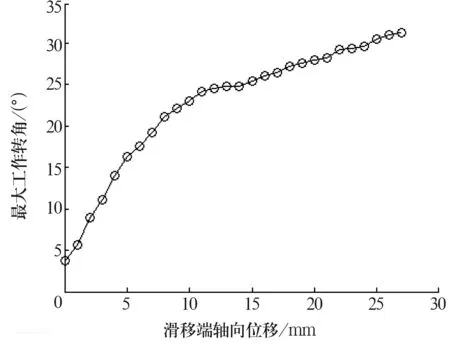
圖2 實際測量滑移曲線

上述問題通過引入模糊算法加以解決。首先，允許相鄰兩段的直線傾角在一定范圍內變化，而仍然認為它們在同一直線上，這樣避免了測量誤差等因素導致的誤判；其次，根據經驗將傾角變化和固定位移間隔分別描述為零、小、中、大等幾個模糊集合，并根據實際操作過程中總結出的模糊規則進行推理計算，得出合適的測量點。

需要指出的是，雖然稱作二次測量法，但幾乎沒有增加整體檢測時間，其將一定的測量點數分配在往返運動過程中，既提高了效率又增加了準確性。

2 模糊控制器設計

首先將傾角變化量Eθ和測量間隔S作為模糊控制器的輸入，其中Eθ=θi+1-θi(θi為首次測量時每段的傾角)，輸出為插值點數N(雖然理想曲線轉折點斜率突然變化，但實際位移曲線卻是一段過渡弧線段，因此將控制器輸出設計為均勻分布的測量點數N)。根據經驗可以確定上述輸入、輸出變量的論域和隸屬函數，其中Eθ和S的論域均為{ZE，PS，PM，PB}(分別代表接近于0、正小、正中、正大)，N的論域為{Z，S，M，B，V}(分別代表接近于0、小、中、大、很大)。它們的隸屬函數分布分別如圖3～圖5所示。由于位移間隔S和插值點數N恒為正值，故其隸屬函數只在正半軸分布。由滑移曲線的特性可知，許用工作角度為位移的不減函數，因此傾角變化量Eθ≥0，但考慮到測量誤差等因素，有可能出現較小的負值，故定義其隸屬函數的分布范圍為[-5，90][4]。

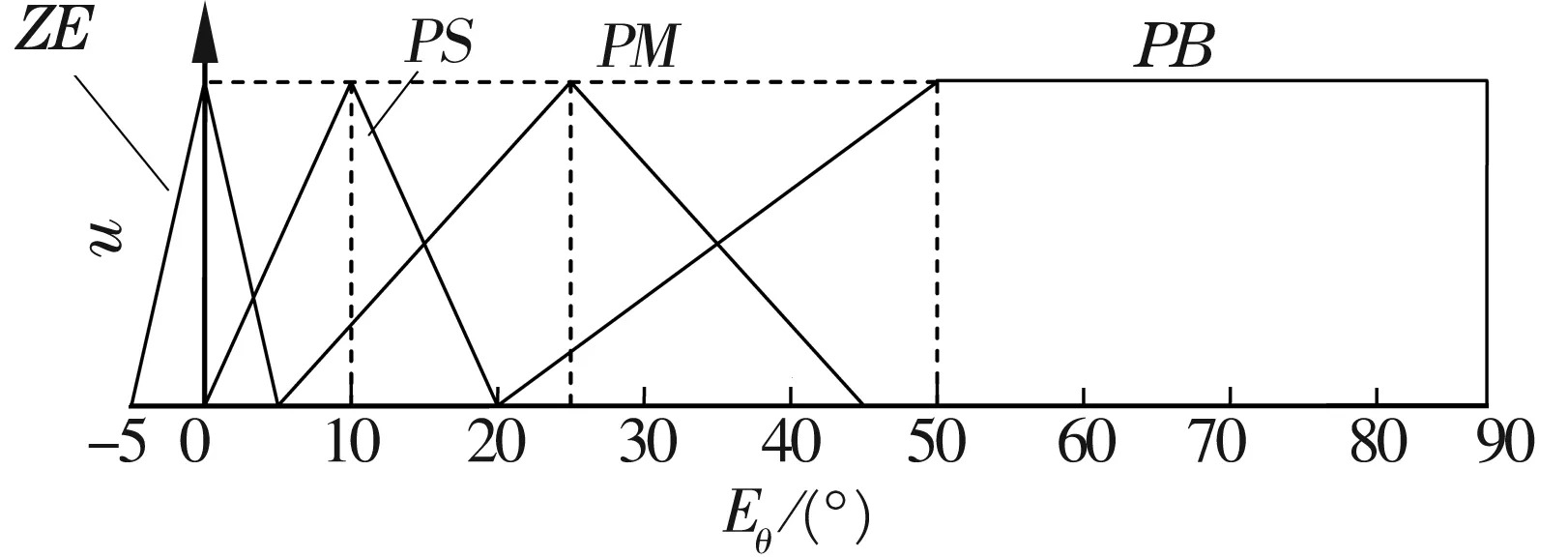
圖3 傾角變化量Eθ隸屬函數

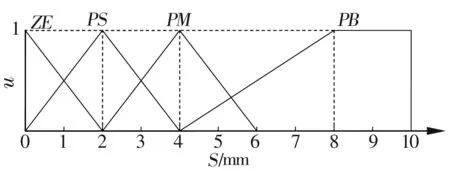
圖4 測量間隔S隸屬函數

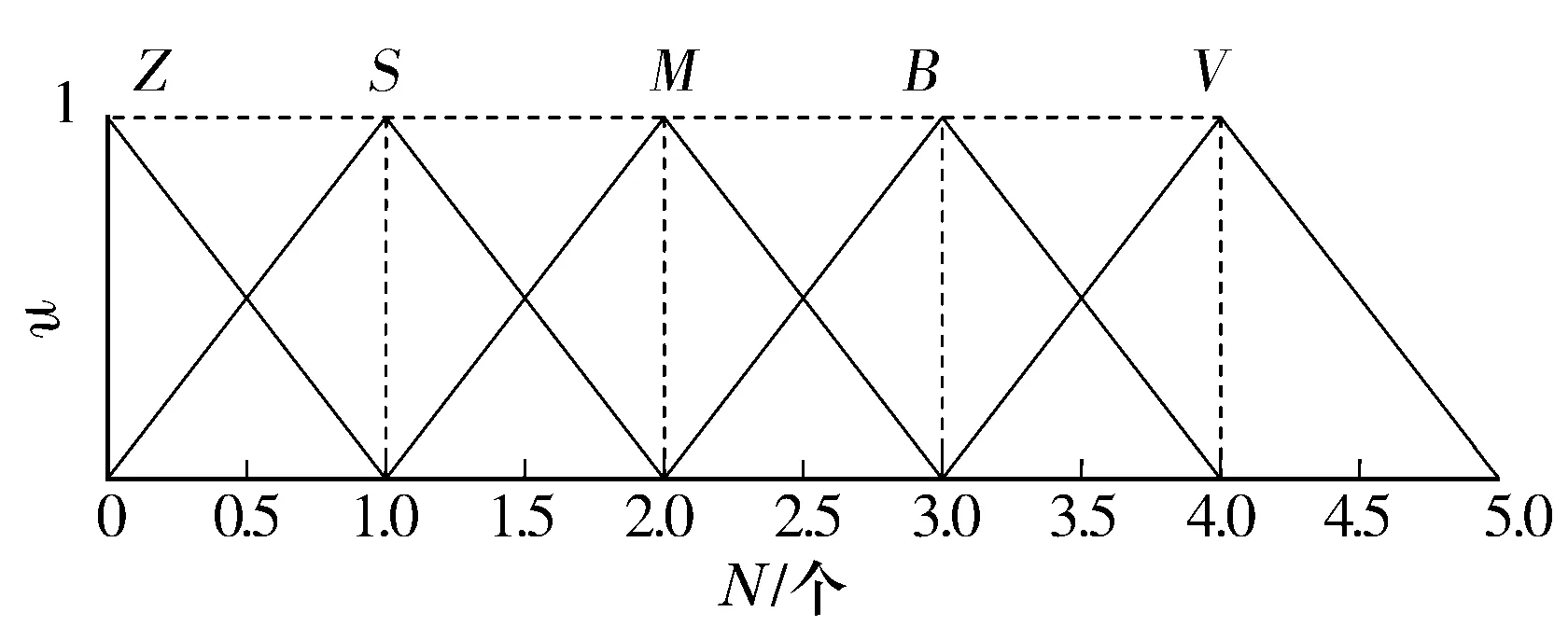
圖5 插值點數N隸屬函數

模糊推理與合成方法采用最大-最小法，解模糊方法采用重心法，見表1。

3 試驗分析

3.1 測控系統結構

研制的等速萬向節驅動軸總成綜合性能測試系統的硬件結構如圖6所示。控制系統采用工控機作為測量控制核心，2個擺動臺上的4個伺服電動機通過伺服驅動器驅動，由多軸伺服運動控制卡(固高GTS-800-PV)進行閉環控制，由伺服電動機的24位增量式編碼器提供反饋脈沖[5]，測試系統位移精度優于3 μm，擺角精度優于0.05°；各個傳感器經變送器后輸入數據采集卡(Advantech PCI-1716)，由測量軟件進行數據處理。

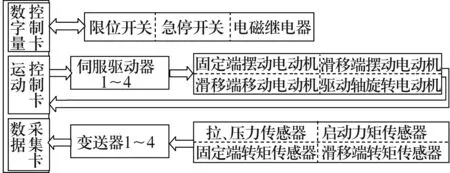
圖6 測試系統硬件結構示意圖

3.2 測量試驗

為驗證提出的模糊測量法的可行性，選用由XLAM005型固定端等速萬向節和XLAM205型滑移端等速萬向節組成的等速萬向節總成在開發的等速萬向節驅動軸總成性能試驗臺上進行了滑移曲線測量試驗。首先采用傳統測量法分別進行了軸向位移間隔為1 mm(圖2)，3 mm(圖7)和5 mm(圖8)的曲線測量，然后利用模糊測量法進行了軸向位移間隔為5 mm的曲線測量(圖9)。作為對比，將1 mm曲線測量結果作為近似的真實曲線。

通過圖2可以看出，真實曲線在0～5 mm和15～27 mm內為直線區域，在5～15 mm內為過渡區域，而傳統5 mm間隔曲線丟失了5～15 mm區域的大量曲線信息，致使曲線產生較大程度的失真；通過圖8和圖9的對比可以看出，利用模糊控制器實現的模糊檢測方法在5～10 mm內增加1個測量點，在10～15 mm內增加2個測量點，檢測曲線得到了顯著改善；通過圖7和圖9的比較則可以看出，雖然都是測量了10個點，但模糊測量法的曲線更逼近真實的曲線。

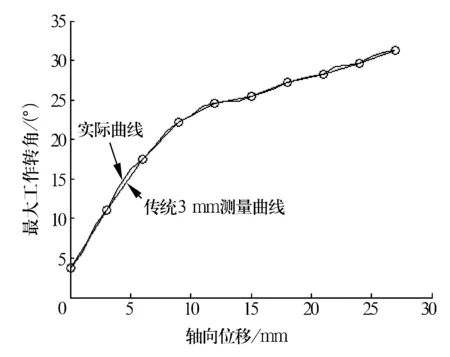
圖7 傳統3 mm間隔測量曲線

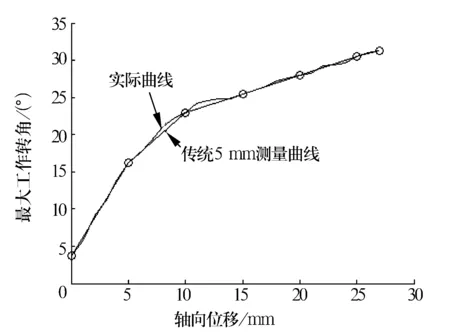
圖8 傳統5 mm間隔測量曲線

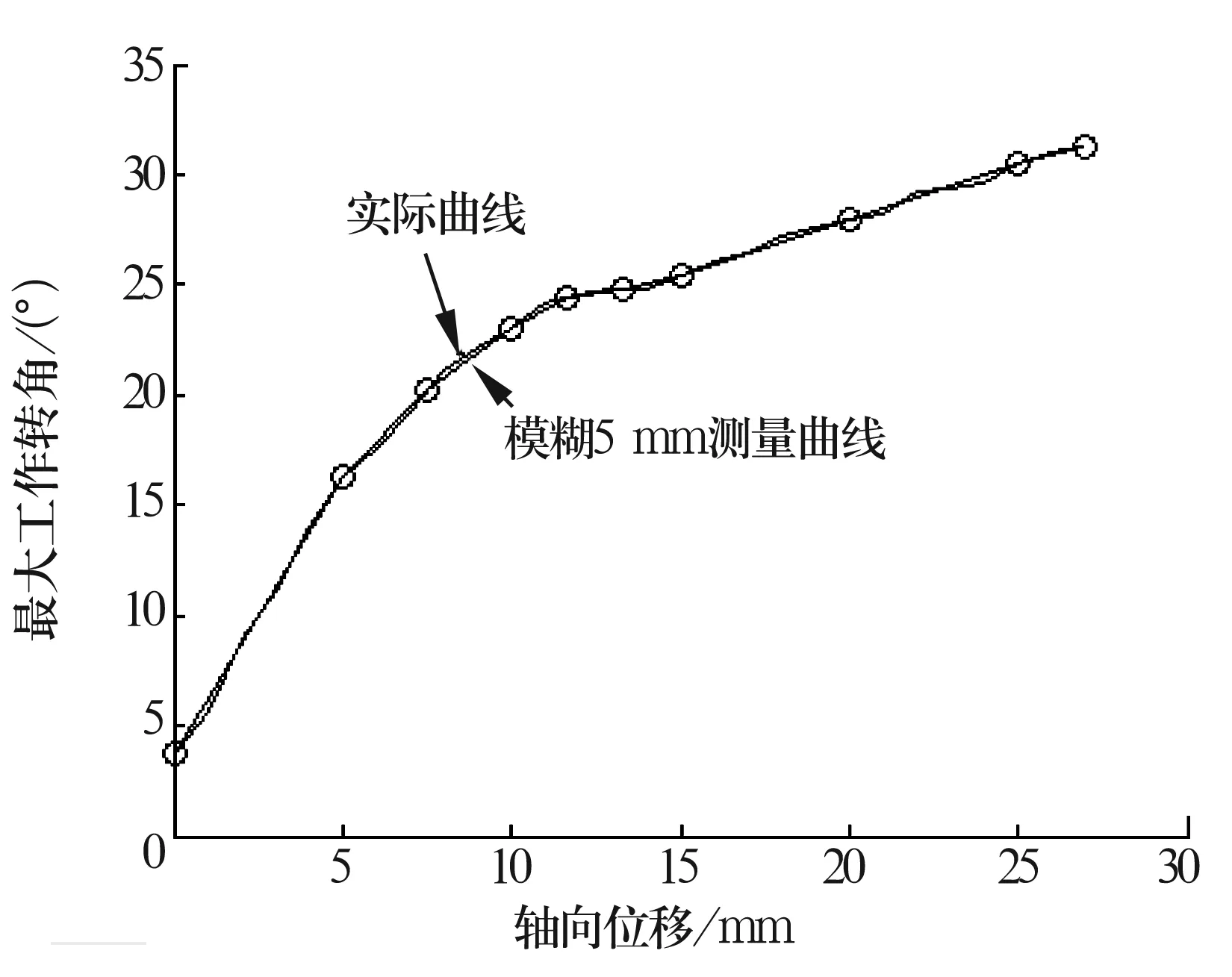
圖9 模糊算法5 mm間隔測量曲線

分別以最大誤差(各測量曲線與實際曲線擺角誤差的最大值)和絕對面積誤差(各測量曲線與實際曲線所圍面積的絕對值之和)2項指標評價所測曲線準確程度，結果見表2。

表2 傳統與模糊測量法精確度對比

通過表2可知，模糊測量比使用同樣測量點數傳統法的最大誤差減小60%，絕對面積誤差減小31.5%；比同樣間隔傳統法的最大誤差減小55%，絕對面積誤差減小52.5%，由此表明模糊測量法能夠更準確測量滑移曲線特征，對傳統測量法有較好的改善作用。

4 結束語

在分析傳統萬向節滑移曲線測量法不足的基礎上，提出模糊算法曲線測量法，并通過試驗證明該方法測得的曲線更加精確，實現了準確度和測量效率的平衡。