指數率水基磁流體滑動軸承微觀熱彈流潤滑分析

史修江，王優強

(青島理工大學 機械工程學院，山東 青島 266033)

磁流體，又稱磁性液體，是一種新型的功能材料，它既有液體的流動性又有固體磁性材料的磁性，故在實際中有著廣泛的應用，在理論上具有很高的學術價值。目前，國內、外對磁流體潤滑的研究取得了一定的成就，文獻[1]分析研究了多孔滲透磁流體滑動軸承，獲得了無量綱壓力、承載能力、摩擦力、摩擦因數和壓力中心位置的表達式。文獻[2]在磁流體滑動軸承的薄膜特性研究中，推導出外加磁場作用下的Reynolds方程，并研究外磁場和Brown Relaxation時間參數對軸承承載性能的影響。文獻[3]研究了磁流體潤滑的非Newton性質。文獻[4]研究了磁流體黏度的影響因素。

隨著綠色化學的發展，水基磁流體日益受到國際社會的廣泛關注。水基磁流體的主要特征是用水作為載液，避免了有機溶劑對環境的污染。同時它還具有價格便宜、超順磁性、生物兼容性和分散性好等特點，在動態密封、自潤滑和研磨拋光等方面有很好的應用前景。用水基磁流體來潤滑滑動軸承，在磁場的作用下，不僅可以實現軸承的連續潤滑，還具有一定的自密封性能。

然而對于水基磁流體彈流潤滑方面的研究尚沒有人涉足，文獻[6]曾經研究過表面粗糙度紋理對Re-Eying 非Newton流體彈流性能的影響。下文將在前人基礎上，研究表面粗糙紋理對指數率非Newton水基磁流體的彈流潤滑性能的影響。

1 指數率非Newton流體

由于水基磁流體磁粉顆粒極小，不需要采用兩相流體模型，用指數率非Newton流體模型分析即可得到滿意的結果[7]。

指數率非Newton流體本構方程為

(1)

式中：u為潤滑膜流體速度；z為膜厚方向坐標。

(1)替換Newton流體中黏度方程為

m=m0exp{(lnm0+9.67)×[-1+

(2)

(3)

式中：m為一個表達黏度的物理量，m0為磁場作用下的環境黏度；mc為水基載液的動力黏度，p為潤滑膜壓力；T為潤滑膜溫度；T0為環境溫度；z0為黏壓系數；s0為黏溫系數；φ為磁粉體積分數；L(α)為Langevin[8]函數。

α=μ0XD3B2/(6K0Tμ2)，

式中：X為磁化率；B為磁感應強度；μ0為真空磁導率；μ為磁導率，文中μ=2μ0;D為磁粉的顆粒直徑；K0為Boltzman系數。

(2)計算剪應力τ

(4)

(5)

(3)由m和τ計算當量黏度η*

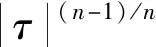
(6)

(4)再用η*代替其余全部數學表達式中的黏度η。

2 彈流潤滑方程

水基磁流體導熱系數為0.586 W/(m·K)，比熱容為4 200 J/(kg·K)；采用錫青銅軸瓦和40Cr軸，軸導熱系數k1=30 W/(m·K)，比熱容c1=670 J/(kg·K)；軸承的導熱系數k2=24.8 W/(m·K)，比熱容c2=343 J/(kg·K)；黏壓系數為2.2×10-8m2/N，黏溫系數為0.042 K-1，穩態載荷F=4 000 kN，軸承寬為0.8 m。

2.1 Reynolds方程

考慮熱效應的Reynolds方程為[9]

(7)

這里新出現的7個表征黏度和密度的變量是由于允許黏度和密度在z方向發生變化而產生的。

(1)p為磁流體潤滑膜壓力，則p滿足載荷方程

(8)

式中：w為單位長度穩態載荷；xin為計算域的起始坐標；xout為計算域的終止坐標。邊界條件：當xin=-4.6b，xout=1.4b時(b為Hertz接觸半寬)，p(xin)=p(xout)=0；當xin≤x*≤xout時(x*為取值范圍內任意值)，p(x*)≥0。

(2)pM為磁場力，其計算式為[10]

(9)

式中：H為磁場強度，H=B/[μ0(1+X)]，磁化率X=1；M為磁化強度；B為磁感應強度，B=20 mT。

(3)ρ為磁流體潤滑劑的密度，密壓密溫計算式為[10]

ρ=ρ0[1+C1p/(1+C2p)-C3(T-T0)]，

(10)

(11)

式中：C1=0.6×10-9Pa-1；C2=1.7×10-9Pa-1；C3=0.000 65 K-1；ρ0為水基磁流體潤滑劑的密度；VC和VP分別為基液體積和固體顆粒體積；mc和mp分別為基液質量和固體顆粒質量。

(4)軸轉速n=500r/min，切向速度U1=

πdn/(60×1 000)=5.2 m/s，軸承速度U2=0，卷吸速度U=(U1+U2)/2 =2.6 m/s。

2.2 膜厚方程

(12)

(13)

式中：h0為剛體中心膜厚；R為當量曲率半徑；E′為綜合彈性模量；Sa為靜止軸承表面粗糙度函數；Aa為軸承表面粗糙峰高；la為波長。

2.3 溫度控制方程

潤滑膜能量方程和兩固體的熱傳導方程為

(14)

(15)

式中：c為比熱容；q為流量；k為導熱系數。

坐標z1=-d，z2=d，d=3.15b。d為軸和軸承的溫度滲透層厚度，m。在入口處逆流區不需要溫度邊界條件。在潤滑膜入口非逆流區，潤滑膜能量方程的溫度邊界條件為：T(xin,z)=0。軸承熱傳導方程的溫度邊界條件為：T(xin、,z2)=T0，T(x,d)=T0；軸熱傳導方程的溫度邊界條件為：T(xin,z1)=T0，T(x,-d)=T0。

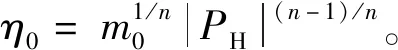
用上述無量綱參數把數學模型中的各方程無量綱化。

3 數值分析方法

用有限差分法離散無量綱后的微分方程，然后用多重網格法求解壓力[11]，用逐列掃描法計算溫度，用多重網格積分法計算彈性變形。多重網格法求解時，網格節點越密數值解的精度越高，但將增加計算量和計算時間。本例在求解壓力時，假定溫度場是已知的，通過解Reynolds方程求出壓力，并用它求得膜厚，通過調整剛體中心膜厚使壓力滿足載荷平衡方程。求解所用的網格共6層，最高層有961個節點。

計算溫度場時，假定壓力和膜厚是已知的，通過解潤滑膜的能量方程和固體熱傳導方程得到溫度場分布。潤滑膜內使用等距網格，節點數為9；固體內靠近固液界面處和遠離固液界面處使用不等距網格，兩固體內未知溫度的節點數均為5。從潤滑膜入口掃描至出口，同時求出21個節點上的溫度。

4 結果分析

4.1 粗糙峰高對水基磁流體彈流性能的影響

圖1～圖3分別是在恒定磁感應強度20 mT、粗糙峰值為0.5，1和2時水基磁流體的無量綱膜厚、壓力和溫度分布圖。

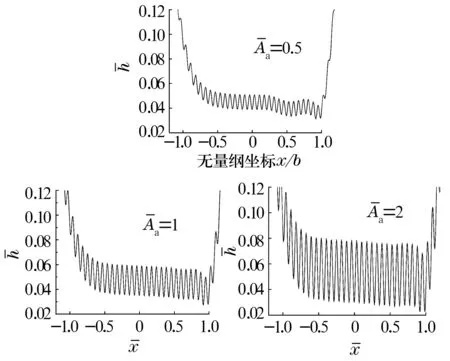
圖1 不同粗糙峰值的膜厚分布

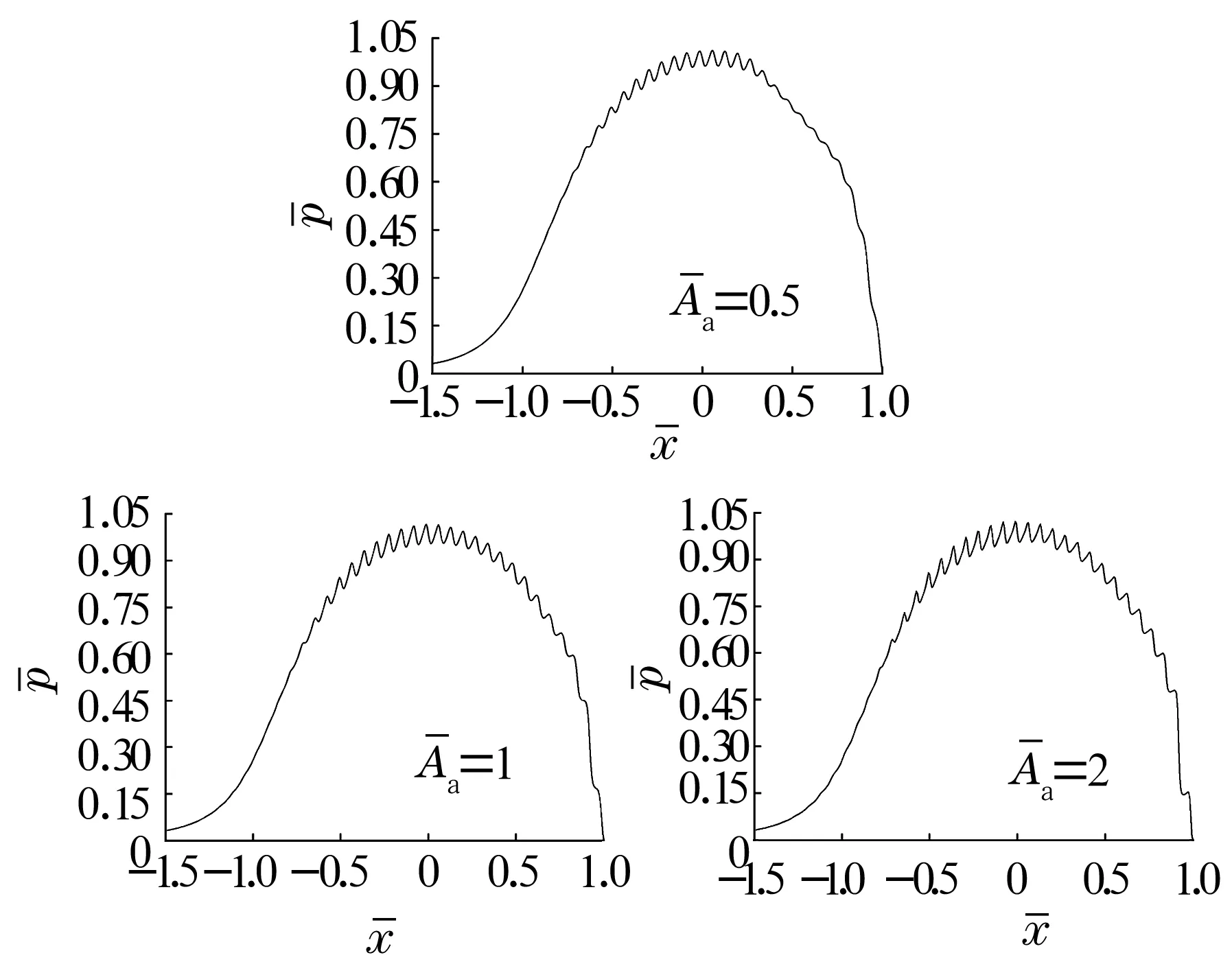
圖2 不同粗糙峰值的壓力分布

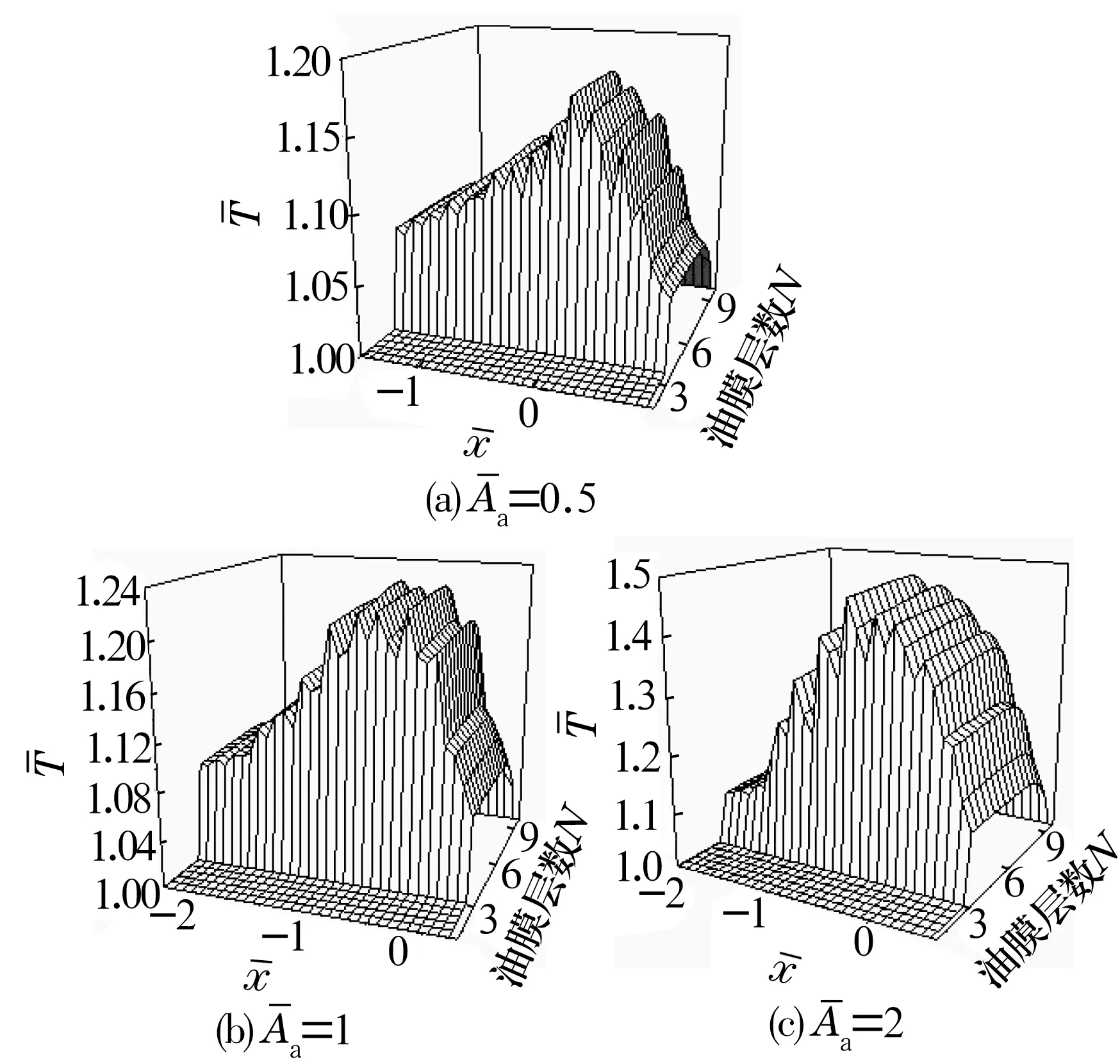
圖3 不同粗糙峰值的溫度分布

由圖1可知，在有粗糙峰的表面水基磁流體的膜厚波動明顯，膜厚波動幅度隨著峰高的增加而逐漸變大，最小膜厚逐漸減小。由圖2可知，水基磁流體的壓力波動明顯，壓力峰波動幅度隨著峰高的增加而增大。由圖3可知，水基磁流體的溫度波動明顯，溫度隨著峰高的增加而變大。這是因為接觸區的油膜是由動壓效應形成的，而每個粗糙峰又會在接觸間隙中產生局部的動壓效應，所以粗糙峰對壓力、膜厚和溫度的影響是一一對應的，粗糙峰對應的油膜處會產生局部的壓力峰、最小膜厚和高溫。

4.2 波長對水基磁流體彈流性能的影響

圖4～圖6分別是在恒定磁感應強度20 mT、波長la為0.15，0.2和0.3時水基磁流體的無量綱膜厚、壓力和溫度分布圖。

圖4 不同波長的膜厚分布

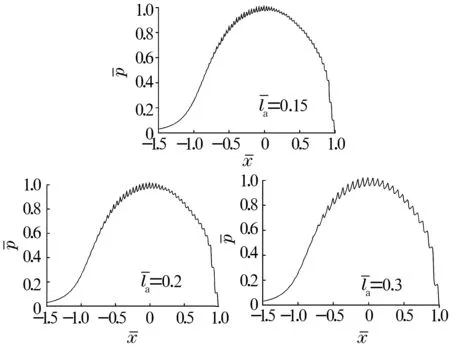
圖5 不同波長的壓力分布

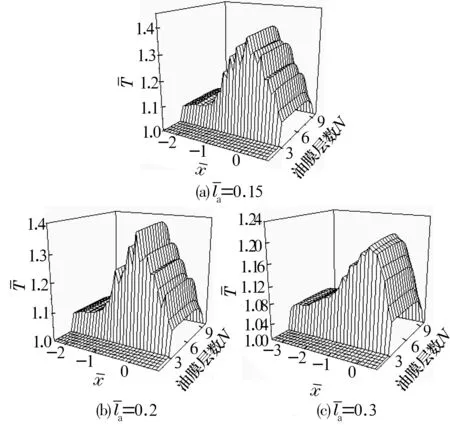
圖6 不同波長的溫度分布

由圖4可知，水基磁流體的膜厚隨著波長增大越來越稀疏，最小膜厚逐漸增大。由圖5可知，水基磁流體的壓力隨著波長的增大越來越稀疏。由圖6可知，水基磁流體的溫度隨著波長的增大逐漸減小。

這是由于相鄰粗糙峰的距離增大，使得相應處產生的局部壓力峰間距變大，從而使相應處膜厚波動距離增大，流入潤滑區的水基磁流體流量增大，動壓效應增強，最小膜厚增大，溫度減小。

5 結論

(1)隨著滑動軸承表面粗糙峰值的增大，水基磁流體潤滑膜的壓力、膜厚和溫度有明顯的變化，壓力波動幅度逐漸增大，最小膜厚逐漸變小，溫度增大。

(2)隨著波長的增大，波數減少，水基磁流體流入潤滑區的量增大，膜厚波動越來越稀疏，最小膜厚逐漸增大，壓力波動越來越稀疏，溫度減小。