全球定位系統衛星位置計算中插值方法精度分析

孫華麗，張政治

（61920部隊，成都 610505）

1 引言

在全球定位系統 （global positioning system，GPS）衛星導航定位時，不管是采用差分模式還是非差精密單點定位，都是利用距離后方交會測量原理，即用戶通過測量接收機到衛星間的距離來確定接收機的位置，于是導航定位的前提是實時獲取衛星的位置和速度，而衛星的位置和速度是由衛星的廣播星歷參數來計算得到的［1］。

由接收機收到的導航電文中開普勒軌道參數和軌道攝動參數等信息按照固的公式計算得到GPS衛星的瞬間坐標，即所謂的直接法，文獻［2］詳細論述了其計算步驟。用廣播星歷直接計算GPS坐標，計算量大，過程復雜，需要在星歷文件與觀測文件之間不停地進行時間比對和衛星比對，效率低。并且由于廣播星歷數據更新周期為2h，用相鄰兩組星歷計算同一時刻坐標時會產生不同結果，這為臨界區域的坐標確定、周跳剔除以及觀測值殘差分析等帶來諸多不便。在實際應用中一般采用插值的方法獲取所需時刻的衛星位置坐標，因此有必要尋找一種計算過程簡便、占用內存小，且滿足精度要求的插值算法將特定時段衛星軌道用某些具有代表性的坐標點標準化。

2 三種常用插值算法

目前在利用廣播星歷計算GPS衛星坐標這一領域，最常用的插值方法是拉格朗日插值，拉格朗日插值模型比較簡單，但當需要進行增減節點時，所有的插值基函數將改變，原有公式必須重新建立，計算量大。當需要提高精度進行高階插值時，可能會產生龍格現象，并且在插值區間端點處容易產生震蕩。三種插值算法簡述為［3］

2.1 牛頓插值

牛頓插值將插值基函數定義成

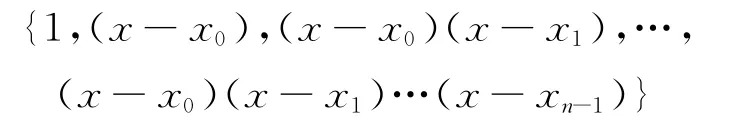
其多項式的系數是各階均差，定義為：

一階均差定義為

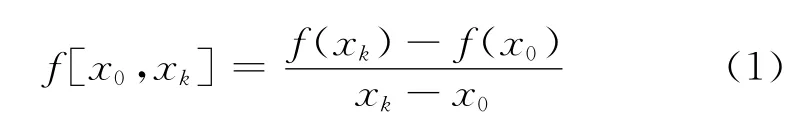
二階均差定義為

類似地，定義k階均差

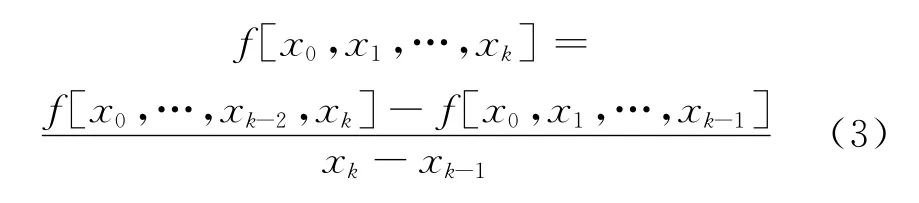
根據均差定義，高階均差是低一階均差的均差。定義牛頓均差插值多項式

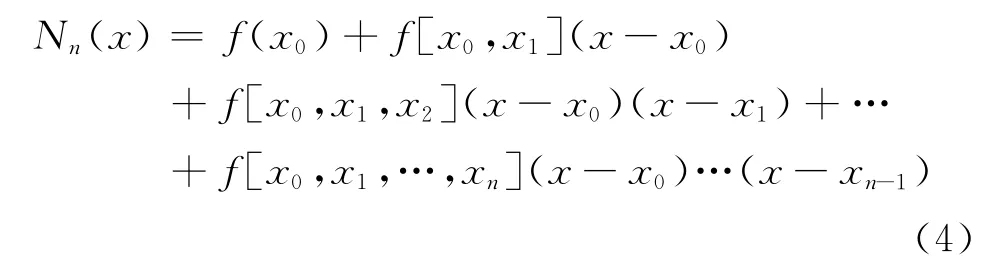
在實際計算中，當增加節點時，只需增加一個被加項，原來計算全部有效。這樣就避免了增減節點引起插值基函數的改變，導致整個公式的變化。

2.2 埃爾米特插值

埃爾米特插值也叫指定微商值的插值，是一種光滑的插值方法，不但要求在節點上函數值相等，而且為了保證光滑程度還要求對應的導數值也相等。首先構造埃爾米特插值多項式，設已知節點

a≤x0＜x1…＜xn≤b上，

yj＝f（xj），mj＝f′（xj），（j＝0，1，…，n），這里給出了2n＋2個條件，可唯一確定一個次數不超過2n＋1的多項式

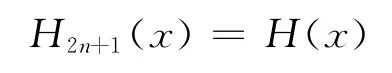
其形式為

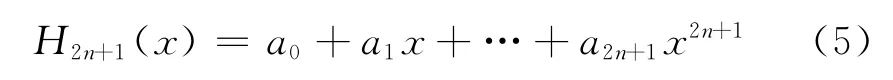
寫成用插值基函數表示的形式

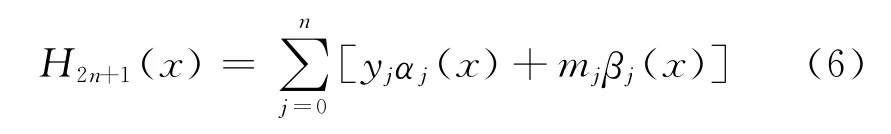
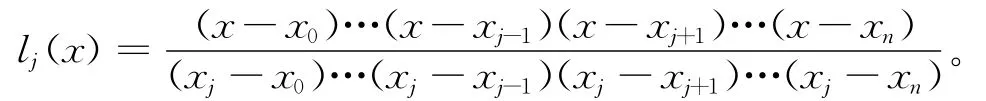
數學上可以證明這種插值函數具有一致收斂性。

2.3 樣條插值

樣條插值能用較低次數的多項式達到較高階的光滑度，若S（x）滿足以下條件：

（1）在給定區間［a，b］上有二階連續導數；

（2）給定節點a＝x0＜x1＜…＜xn＝b，在每個小區間 ［xi，xi＋1］上，S（x）是三次多項式。

稱滿足以上兩個條件的函數S（x）為節點x0，x1，…，xn的三次樣條函數。

若在節點xj上給定函數值

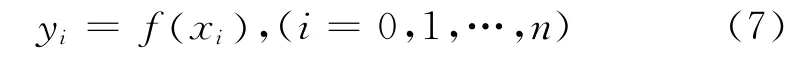
且S（x）＝yi，i＝ （0，1…，n）成立時，則稱S（x）為節點x0，x1，…，xn的三次樣條插值函數，其中x0，x1，…，xn為樣條節點。三次樣條表達式為

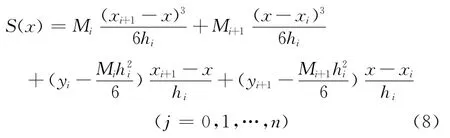
Mi在力學上解釋為細梁在xi截面處的彎矩，稱為S（x）的矩。文獻 ［4］通過M，T關系式法構造五次樣條插值函數。

3 三種算法插值計算GPS坐標

3.1 數值實驗

利用PRN1衛星在2007年5月7日歷元時刻10時的廣播星歷參數文件，直接法可計算出9時至10時30分之間的相關坐標值。本文等距選取插值節點時刻為9h：15m：10h30m作為訓練集，記作節點0：15：90，這樣選取的歷元時刻是整分鐘，可以避免出現小數位，導致插值時出現浮點運算，降低了計算復雜度，這也是采用偶數階插值的原因。等距選取測試歷元時刻為9h：5m：10h30m，記為節點0：5：90。

由于直接法得到的坐標值是離散的，因此在埃爾米特插值和樣條插值中，補充導數條件不能由直接法給出，現有的研究表明8階拉格朗日插值誤差達到厘米級［5-8］，可以滿足GPS普通用戶的應用需求，于是這里可以借助8階拉格朗日插值多項式對插值節點求各階導數作為補充條件。在進行誤差統計分析時，由于正負誤差效果等同，均先將原始誤差值取絕對值，并且根據插值的定義，這里還要剔除誤差曲線插值節點處的零值。

在牛頓插值中，利用7個節點構造6階牛頓均差插值。在測試集點0：5：90上，將6階牛頓均差插值廣播星歷所得坐標與直接法計算出來的真值做比較，圖1給出了三個方向上的誤差分布曲線，表1列出了三個方向上的誤差統計情況。

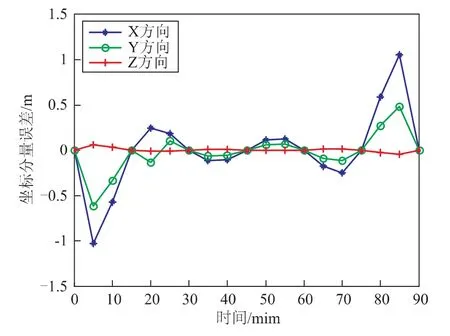
圖1 6階牛頓插值誤差曲線

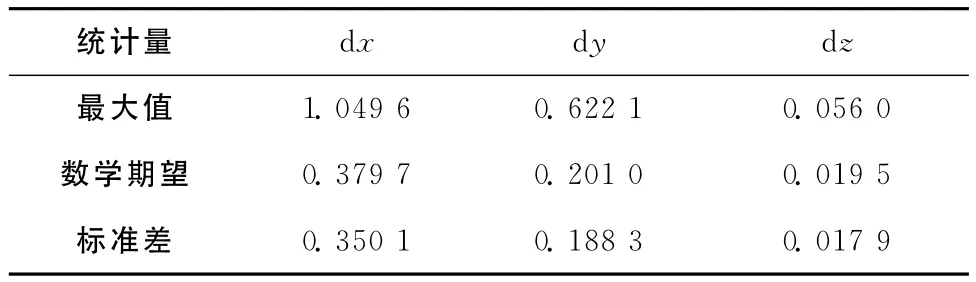
表1 6階牛頓插值誤差統計/m

同樣的方法，在節點0：15：90的基礎上，通過直接計算追加兩個節點，共9個歷元時刻作為訓練集節點，構造8階牛頓均差插值多項式。在測試集點0：5：90上，將8階牛頓均差插值廣播星歷所得坐標與直接法所得結果做比較，圖2給出了三個方向上的誤差分布曲線，表2列出了三個方向上的誤差統計情況。

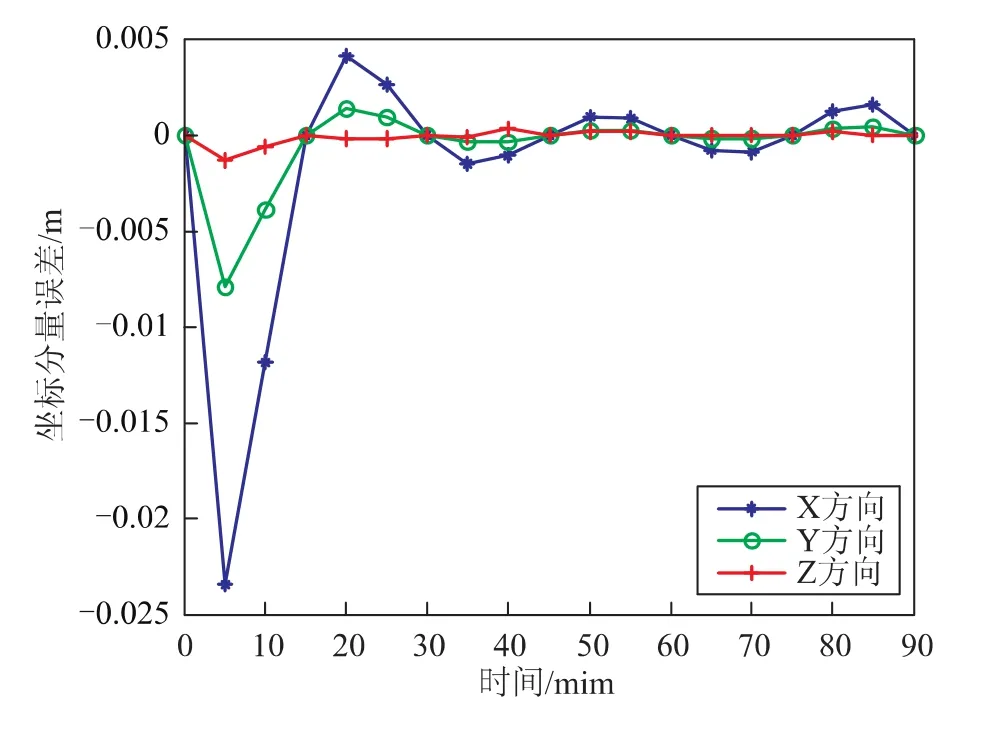
圖2 8階牛頓插值誤差曲線

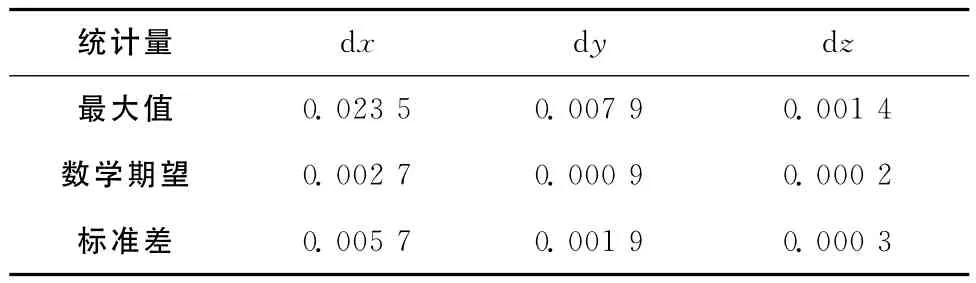
表2 8階牛頓插值誤差統計/m

在埃爾米特插值計算中，本文考慮插值精度的要求和便于比較，筆者在訓練集節點上分別構造了三點5次和四點4次埃爾米特插值多項式，并應用于衛星軌道插值。在測試集點0：5：90上分別將分段5次和7次埃爾米特插值所得結果與直接法計算出來的真值做比較。圖3給出了5次埃爾米特插值在三個方向上的誤差分布曲線，表3列出了5次埃爾米特插值在三個方向上的誤差統計情況，圖4和表4給出了7次的情形。

圖3 5次埃爾米特插值誤差曲線

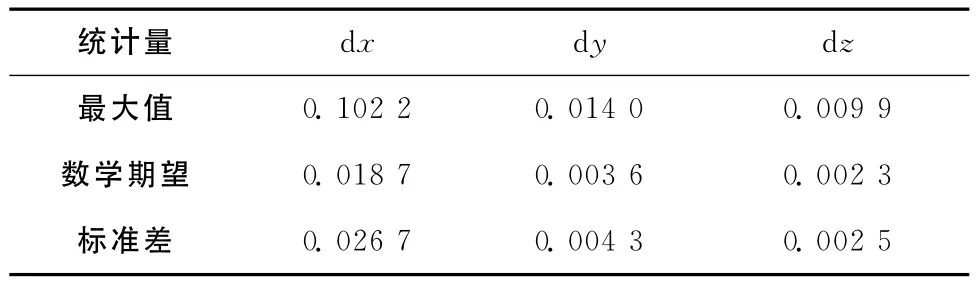
表3 5次埃爾米特插值誤差統計/m

圖4 7次埃爾米特插值誤差曲線

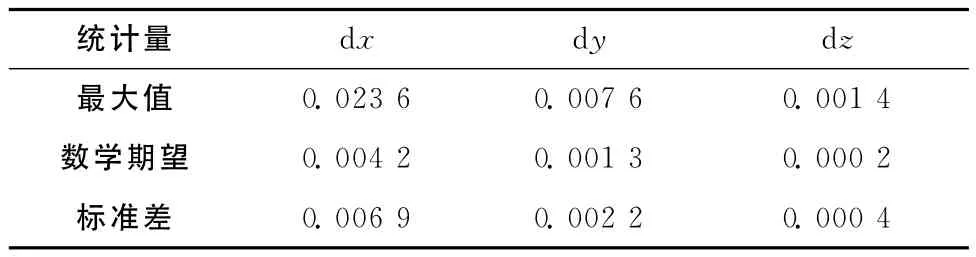
表4 7次埃爾米特插值誤差統計/m

在樣條插值中，筆者嘗試了3次樣條插值和5次樣條插值，在測試集點0：5：90上，將3次樣條和5次樣條插值結果與直接法計算出的真值做比較。圖5給出了3次樣條插值在3個方向上的誤差分布曲線，表5列出了3次樣條插值3個方向上的誤差統計情況，圖6和表6給出了5次的情形。

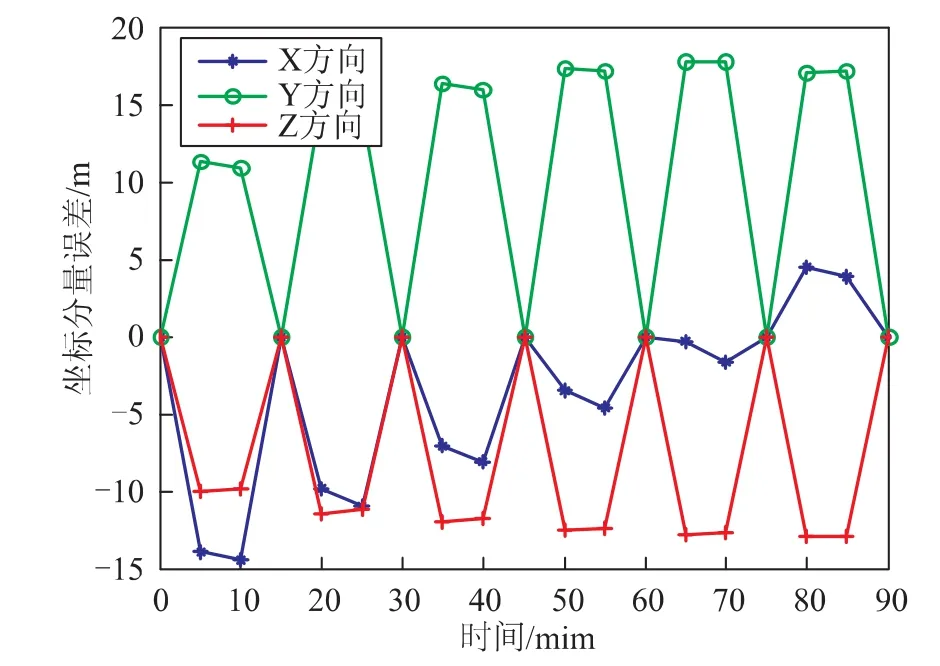
圖5 3次樣條插值誤差曲線

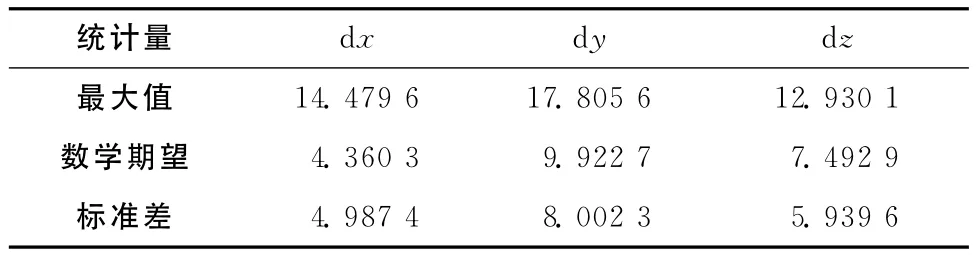
表5 3次樣條插值誤差統計/m

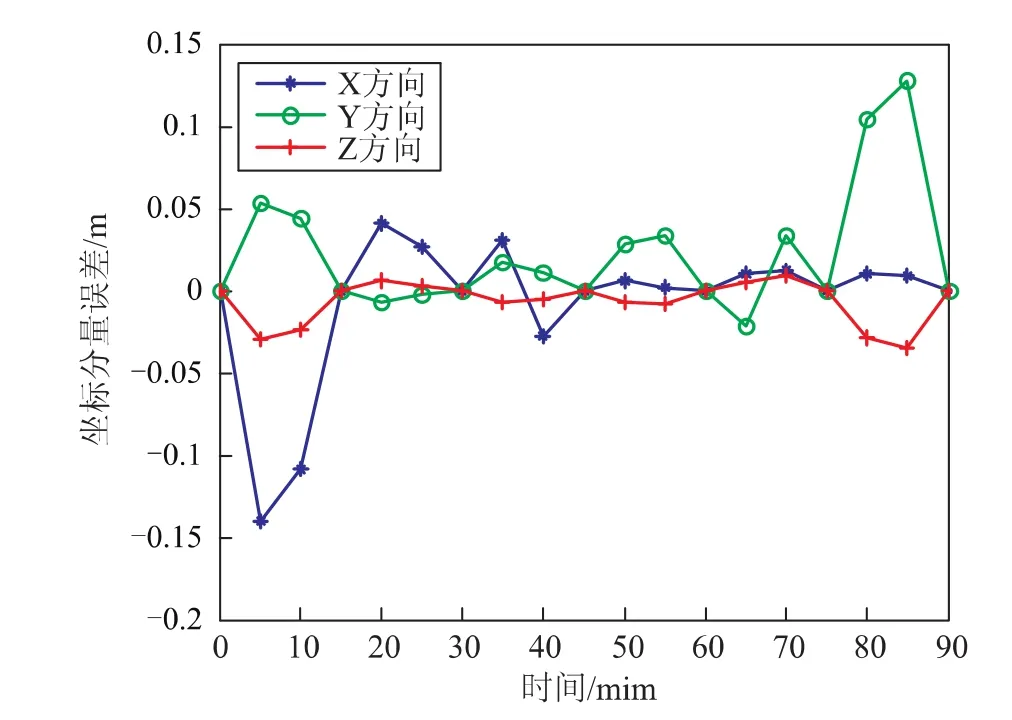
圖6 五次樣條插值誤差曲線

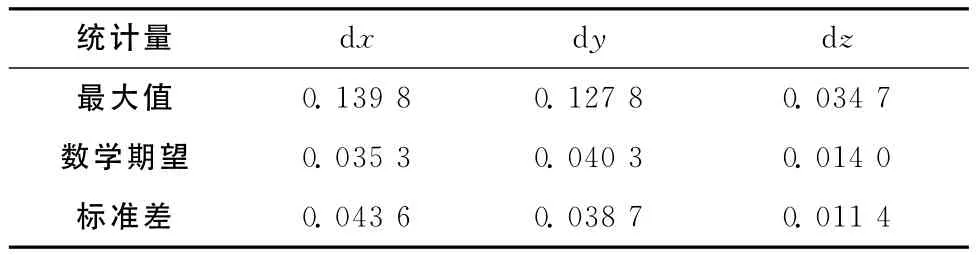
表6 五次樣條插值誤差統計/m

為了考察三種插值方法插值結果與直接法所得真值的離散程度，綜合考慮階數和精度的要求，下面選取6階牛頓插值、5次埃爾米特插值、五次樣條插值來計算在節點處的均方根 （root mean square，RMS），其公式是

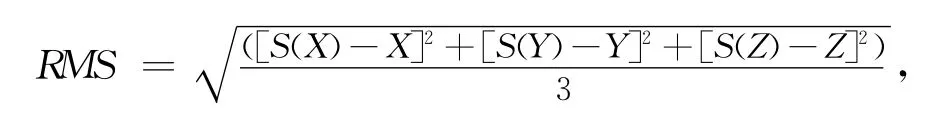
在同一坐標系中畫出三種方法的RMS分布圖如圖7所示。

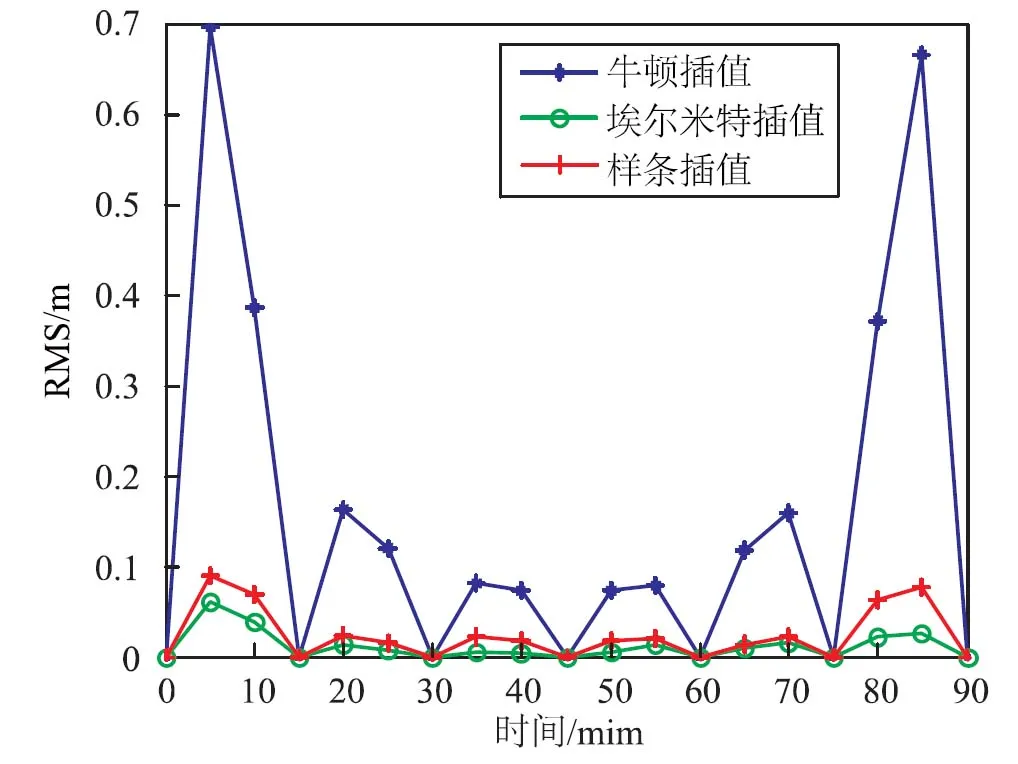
圖7 三種插值方法的RMS分布圖

3.2 精度說明

由圖1和表1可知，6階牛頓插值在Z方向上精度最高，達到厘米級，Y方向次之，為分米級，X方向僅為米級。由圖2和表2可知，8階牛頓插值在Y、Z方向上都達到了毫米級，X方向達到了厘米級。8階有小幅震蕩，6階的震蕩現象比較嚴重。三個方向上在插值區間中間部分精度都比端點出高一個量級，與插值的計算特點相符，下面埃爾米特插值和樣條插值的結果也有類型的現象。

由圖3和表3可知，五次埃爾米特插值在X、Y、Z方向精度分別為分米、厘米、毫米。由圖4和表4可知，7次埃爾米特插值誤差在X方向為厘米級，Y、Z方向達到毫米級。三個方向在插值區間左端點處仍有較明顯的震蕩現象。

由圖5和表5可知，3次樣條插值的計算精度在十米級，不能滿足用戶的精度需求，但是沒有震蕩現象發生。由圖6和表6可知，5次樣條插值精度在X、Y方向為分米級，在Z方向為厘米級，在插值區間端點處震蕩現象較不明顯。

由圖7三種插值方法的RMS分布圖知，區間內精度較高，區間端點處會產生震蕩。牛頓插值誤差斜率變化比較大，震蕩現象最為嚴重，而隨著插值階數的提高，震蕩也會更嚴重。埃爾米特插值比較好的處理了區間端點處的震蕩問題。

3.3 結果分析

拉格朗日多項式在增加新的節點時，原有基函數需要重新計算，而牛頓法通過構造差商，在加入新節點后，只需計算一次更高階的差商，原有差商結果仍可繼續使用，解決了動態增加節點的問題，使迭代方式具有承襲性，程序實現靈活，但其精度不高。

用分段低次埃爾米特插值可以做到降低插值階數情況下提高插值精度，這樣可以降低計算復雜度，降低了插值多項式階數還可以進一步避免了龍格震蕩現象的發生。增加1個節點時，埃爾米特插值可以提高2個階數，并且由于采用分段低次處理插值問題，可以較好的避免拉格朗日多項式在增加新的節點時，原有基函數需要重新計算的問題，只需局部改變多項式基函數，模型變化小，易于程序移植。

5次樣條插值方法模型簡單，精度高，可克服分段插值函數整體光滑性較差的缺點，同時計算復雜度比牛頓插值和埃爾米特插值降低了一個階［4］。5次樣條插值方法采用分段處理插值問題，各段都是相對獨立的，并且不涉及插值基函數，插值函數表達式形式固定，只需解方程求出區間內樣條節點的二階和四階導數值，較好的解決了動態增減節點的問題，程序實現靈活。

4 結論

三種插值方法各有特點，牛頓插值承襲性較強，但是精度沒有得到明顯提高，適應于衛星有限、點位快速計算且無需高精度；埃爾米特插值精度高，在節點處具有一階光滑度、整體逼近效果好并且一致收斂，適用于較多衛星位置計算或局部軌道計算；樣條插值在穩定性、震蕩性方面有其獨特的優勢，適合于軌道弧段邊界點的位置計算。在利用GPS廣播星歷對衛星軌道進行插值計算中，上述三種方法在一定程度上可以替代傳統的拉格朗日插值方法，在一定范圍內值得推廣。

［1］魏子卿，葛茂榮.GPS相對定位的數學模型［M］.北京：測繪出版社，1998.

［2］HOFNM ANN－WELLENHOF B，LICHTENEGGER H，COLLINS J.GPS Theory and Practice.Wien：Springer－Verlag，1997.

［3］李慶揚，王能超，易大義.數值分析［M］.4版.北京：清華大學出版社，2005.

［4］唐建國，蔣九林.五次樣條函數的構造［J］.鄭州大學學報：理學版，2005，37（3）：15－18.

［5］江國焰，李明峰，朱振宇，等.GPS衛星廣播星歷的Lagrange等距插值算法［J］.南京工業大學學報：自然科學版，2008，30（1）：34－38.

［6］萬亞豪，張書畢，侯東陽.基于GPS廣播星歷的衛星位置擬合精度分析［J］.測繪工程，2011，20（3）：36－40.

［7］陳劉成，韓春好，陳金平.廣播星歷參數擬合算法研究［J］.測繪科學，2007，32（3）：12－15.

［8］萬亞豪，張書畢，侯東陽.基于GPS廣播星歷的衛星位置擬合精度分析［J］.測繪工程，2011，20（3）：36－40.