讓“美麗的錯誤”裝點出“鮮活的課堂”——一道試題的錯誤生成與反思應對

☉江蘇省徐州市侯集高級中學 陳小祥

數學學習的過程，一定程度上說是一個不斷犯錯和糾錯的過程，學生是課堂的主體，同樣也應是糾錯的主體，如何利用寶貴的錯誤資源，抓住學生錯誤中的合理成分，挖掘錯誤成因，尋找解決策略，使得解題教學更生動活潑，又效果顯然？本文試圖從一道高一測試題的講評案例出發對此做一些探索，不當之處敬請指正.

一、試題講評實錄

有這樣一道高一數學測試題（學生已經學過三角函數、基本不等式等內容）：

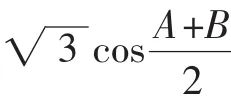
（1）求角C；（2）求△ABC面積的最大值.

教學思路設計：從三種源于學生試卷中的典型錯誤出發，引導學生去思考、辨析、探究、討論，找出錯因，尋求解法，總結策略，完善認知結構，課前請三位同學在前后黑板上分別板演好典型解題過程.

1.典型錯誤之不等式應用不到位

教學主要針對第（2）問，由（1）根據余弦定理可得a2+b2-ab=c2；又a+b+c=12，所以a2+b2-ab=［12-（a+b）］2，化簡得

師：請同學們看思路A，其結果是否正確，過程有沒有問題，是否嚴謹？

生1：結果是對的，過程看不出明顯問題，我認為是對的.

師：還有沒有不同意見？（等待）

師追問：為什么不能這么做，這不是對不等式中取等條件的運用么？

生2：要用不等式求最值，必須考察“正、定、等”這三個條件，這里并無“定”的形式出現，所以用不等式是無意義的.

師：非常好，你能舉例進一步說明不能這么做的原因么？（學生思考，教師可啟發）

師：非常好，生2舉例說明了這樣做是不對的，但為什么不對呢？還有其他的解釋嗎，即為什么不能將取等條件當成新條件代入運算？（視情況可以讓學生討論探究一下，多讓學生發言，之后再由教師精講）

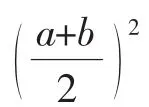
師：非常好，解釋得很清楚，有興趣的同學課后再研究，那么就不能用不等式解了么？

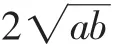
師：很好（停頓一會供學生反思理解），還有應用不等式求解的么？

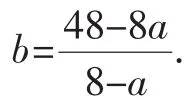
又 0＜a，b＜12，可解得 0＜a＜6，

令 8-a=t，則t∈（2，8），a=8-t，

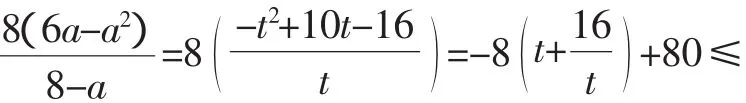
當且僅當t=4，即a=b=4時取等.

師：非常好，你是怎么想的？

生4：要求二元目標式的最值，想到消元思想，結合條件得到其關于a的函數關系式，界定定義域后，根據式子的結構特征，嘗試用一次式表示二次式，代換后發現符合使用不等式求最值的條件“正、定”，考察取等號后得到了最值.

師：這里應用的基本不等式求最值與上法中對基本不等式的應用有何區別？

師：很好，通過上面的論述，我們可做如下小結：

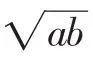
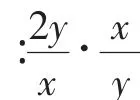
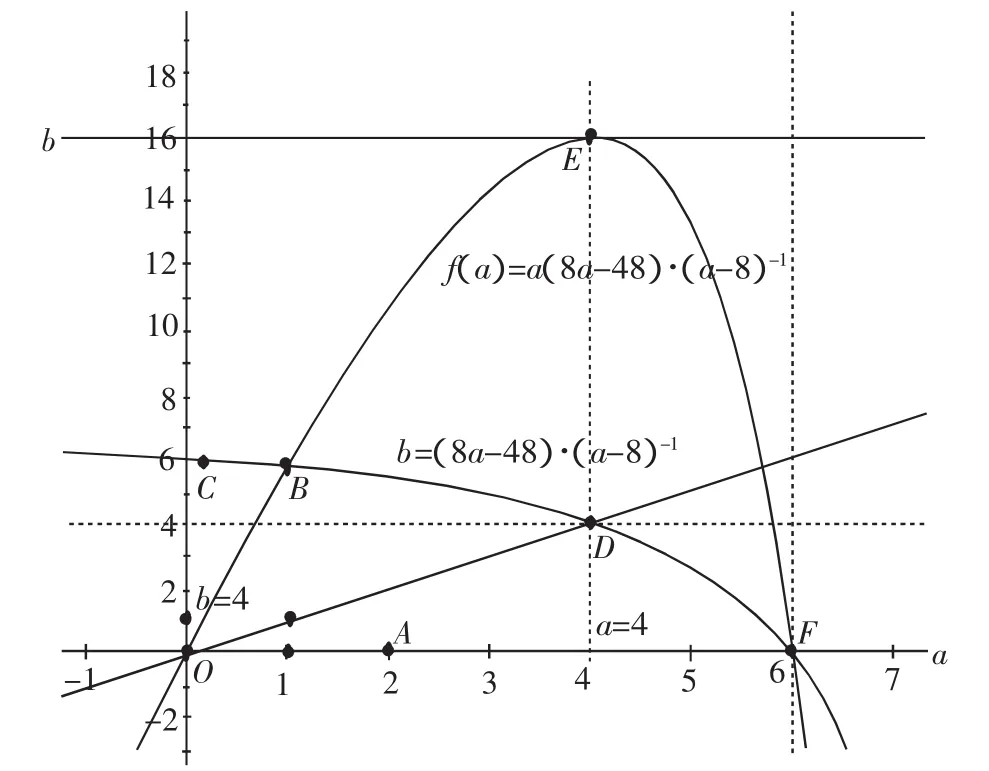
圖1

2.典型錯誤之函數轉化不徹底

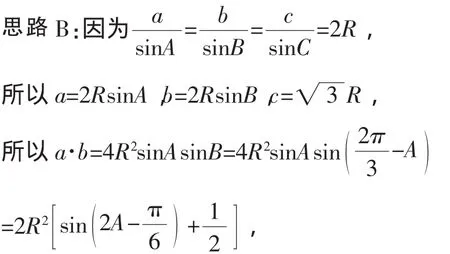
師：請看，這種解法是否正確，為什么？（學生思考，議論）

師：有道理，那怎么辦？能否將R也化成關于∠A的函數呢？

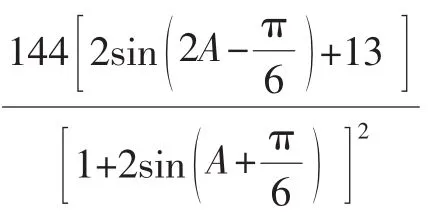
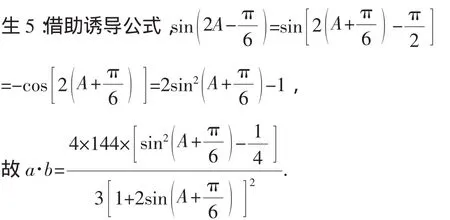
師：很好，利用三角函數中“化異為同”策略，使得式子更簡潔，接下來怎么辦？

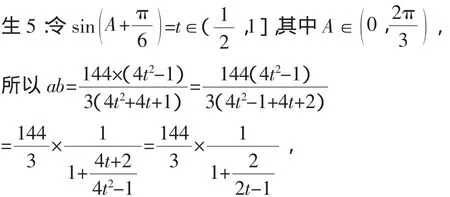
即a=b=c=4.

師：非常好，步步為營，環環相扣，兩次運用正弦定理將二元目標式轉化為了關于∠A的一元函數式，再根據式子結構，利用誘導公式化繁為簡，化異為同，再代換后分離常數進一步簡化式子結構，最后結合參數范圍和函數單調性求出最值，思路明確，基本功扎實，值得大家學習，此種思路下有沒有簡單些的方法？

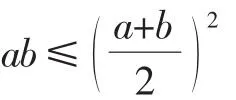
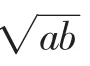
師：真不錯，很明顯解決過程簡化了許多，你能說說這兩種解法的聯系和區別嗎？

生10：兩種方法其實都用到了減元思想，都將二元（多元）的目標式轉化為單元函數式，都涉及了使用正弦定理進行“邊化角“處理，生6的解法其實是結合基本不等式先采用“一次和式”的邊角轉化求最值后再求原目標式的最值，結構上比“二次積式”的邊角轉化要簡單些，所得式子的最值求解也就簡單些.

師：分析得很好（如學生說不到，師再補充），還有要補充的嗎？

生7：老師，我是這么想的：

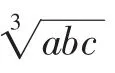
當且僅當a=b=c=4時取等，

師：很好的思路，同學們看有沒有問題.

生8：我有疑問，求解中，他將分子abc取到最大值的條件，直接用于求出其外接圓直徑，代入比式求得面積值，我覺得這不合理，因為除非分子取最大時分母取到最小，這樣比值才最大.

師：嗯，很有道理，那怎么解決呢？

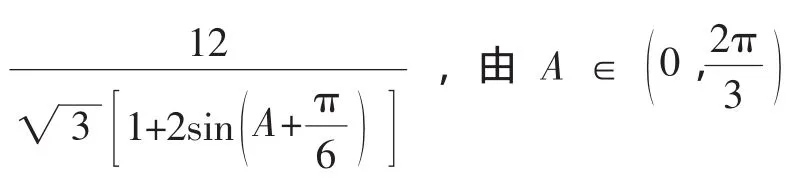
師：非常好的補充，這樣原解法才完整，將掌聲送給他，謝謝他的精彩闡述（掌聲）.

師：很明顯這幾種方法都涉及了一種常用的求二元目標式最值的方法——目標函數轉化法，利用條件將目標是減元后轉化為一元函數，再結合具體情況選擇方法求最值.

3.典型錯誤之數形結合不嚴謹

思路C：如圖2.

圖2

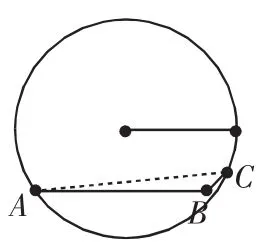
圖3

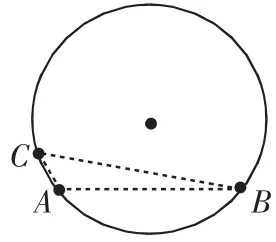
圖4

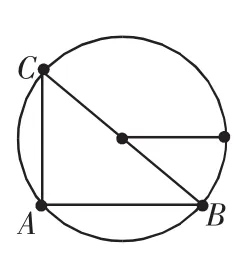
圖5

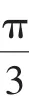
師：你們怎么看這種解法？有無問題？為什么？（留時間給學生思考探討，一番問答后）

生9：看似正確，但依上面的解法，

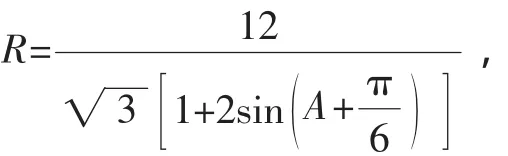
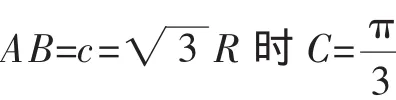
師：非常好，（留學生反思時間）那怎么辦呢？

生9：看來數形結合解不出來，那只能回到前面的解法中去.

師：那我們退一步，你能改變條件使得可以使用類似的幾何法嗎？

師：很及時的變化，非常棒，從上面的不同錯誤及其辨析過程以及多種解法的角度我們可以總結一下二元（多元）目標式最值求法的一般策略：不等式（基本不等式及變式、柯西不等式等）、線性規劃及相關知識、一元函數轉化等方法是高中多元函數式最值問題求解的常用策略，大體上可分為數與形兩類，從數的角度看多將多元目標式劃歸為一元函數式，或者利用不等式直接求最值；從形的角度則多從條件出發尋求目標式或其變形式的幾何意義如：為面積、距離、斜率等或劃歸為線性規劃問題求解，更多的時候往往綜合靈活運用以上策略以順利求解.下面請同學們整理反思這些解法，并完成下列相關練習：

（1）已知x>0，y>0，x+2y+2xy=8，則x+2y的最小值為______；xy最大值為______.

（2）已知x>0，y>0，4x2+y2+xy=1，則 2x+y的最大值為______；xy最大值為______.

（3）已知x>0，y>0，2x+8y-xy=0，則x+y的范圍是_____.

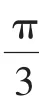
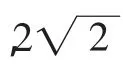
二、常用的錯誤應對策略

①充分預設，以誤引辯，辯在重點難點處.教師需充分篩選研究典型的、普遍的、有價值的錯誤，在課堂上通過各種方式引導學生于重難點處辯論，注意調控辨析走向，務必保證找準問題，辨清矛盾，得到確解.不同想法的碰撞不僅能凸顯問題的內在價值，而且會使得學生的知識和能力在辨析中內化和提升；

②動態生成，示誤引思，加深知識方法理解.教學應該是預設與生成的統一，生成才是課堂迷人的地方，因為總會有出乎你意料的想法出現，而當學生探究、評論有誤時，教師可以將其看成新的資源，繼續誘其深入，引其自糾，培養求異思維.如有必要還可繼續通過一題多解等形式將學生思維引領至更高的層次，引導學生糾正反思錯誤，進而總結知識方法，以加深理解；

③變式教學，糾錯鞏固，促進認知結構完善.通過適當的一題多解、一題多變與多題一解的題組教學與練習讓學生體會到變和不變之間的聯系，加深學生對各種解法及相關知識的深入理解，從而構建更完善的認知結構；

④二次練習，強化認識，防止錯誤反復.一周內再次給出關于典型錯誤的二次練習非常必要也非常有效，視情況再進行教學設計乃至三次練習，適度的重復練習對應試必要而有效.

綜上，教師應積極面對學生的錯誤，認真收集、整理、篩選有價值的錯誤資源，選擇合適的時機和方式，引導學生去辨析、思考、交流、探究、糾錯、拓展和反思，讓學生的思維在解題教學課上動起來、活起來，進而促進新的認知結構的完善和解題能力的提高.

1.張愛珠.淺談高中學生數學思維障礙及對策［J］.福建教育學院學報，2006（6）.

2.黃彩祥.高中數學解題心理性錯誤分析［J］.河北理科教學研究，2003（3）.

3.吳衛東.開啟從錯誤中學習的新視角［J］.新課程周刊，2009（3）.