因圖致誤問題的再思考

☉江蘇省姜堰市第二中學 丁連根

一、問題提出

《數學通訊》2012年第6期35頁一文《解法大同小異，結果大相徑庭》對問題217提供兩種解法，但是，結果卻不相同，誰是誰非？問題的癥結又在何處呢？

二、錯因剖析

通過分析，除給出的解法1和解法2之外還可以有第3種解法，我們可以利用解法3來檢驗解法1和解法2的正確性.

圖1

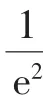
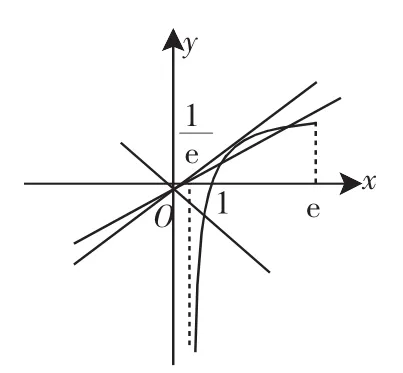
圖2

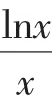
由此可見，問題的癥結在于“圖形”，解法1是“因圖致誤”，作圖時沒有把握住圖形的基本特征和關鍵點，簡單處理，想當然地得出答案，錯誤就在所難免了.

三、解法再探

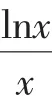
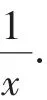
通過求導發現，解法5本質上與解法2是相同的，而解法4中導函數中仍然含有“lnx”，導函數的零點無法直接求出，進一步研究的價值不大.

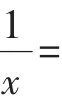
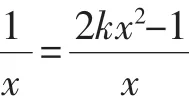
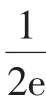
細細算來，這種解法要分8種情況進行討論，研究這種解法對于提高學生分類討論的能力，培養解題的意志品質有很好的幫助.

四、解后反思

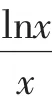
那么學生在解題時應該如何進行合理的選擇呢？我覺得首先要看函數的圖像是不是容易畫出，而容易畫出來的圖像又要看交點是否可以方便研究，如果是不熟悉的函數那就要看這個函數的性質是否方便研究，否則解題就解不下去.畫圖通常要遵循以下的幾個步驟：

1.確定定義域，也就是確定函數圖像的區域；

2.研究函數的性質：奇偶性、單調性、周期性等；

3.畫出關鍵點和關鍵線，如漸近線，對稱軸等；

4.根據函數的性質畫出草圖.