關注特征巧變形 有效拓展顯功能

☉江蘇省新海高級中學 王廣余（特級教師）

在數學課堂教學中，選擇課本中的典型例題（或習題），恰當實施探究與拓展是新課程背景下富有實效的創新教學，是提高學生思維水平、追求高效課堂的重要途徑，是變“教教材”為“用教材”、變“教結論”為“教過程”、創造性地使用教材的根本體現.下面呈現給大家的正是筆者研讀教材、悉心備課時，對一道不等式證明題進行變式探究、拓展創新的過程.

題目：普通高中課程標準實驗教科書（蘇教版）選修2-2第84頁練習第3題（直接證明與間接證明練習題）：

一、剖析原題證法，為后繼猜想奠基

由于要證的不等式是四個無理數的和式，用綜合法證明感覺困難，因而課本采取了分析法證明：

若注意到3-2=6-5的特點，可得到如下簡捷證法：

二、關注原題特征，猜想一般結論

題目看似簡單，但證明后總覺意猶未盡，從證法2可知隱含條件 3-2=6-5（即 2+6=3+5）及 2＜3＜5＜6 起到了關鍵作用，由此我們可想到把不等式一般化，猜想其一般結論.

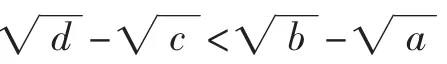
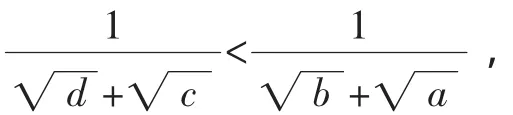
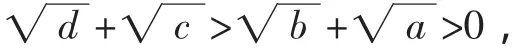
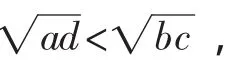
即ad＜bc.

令a+d=b+c=k＞0，

則ad-bc=a（k-a）-b（k-b）=（a-b）［k-（a+b）］，

由a+b＜a+d=k，知k-（a+b）＞0，又a-b＜0，

所以ad＜bc，故原不等式成立.

證法 3：同證法 2，即證ad＜bc，令b-a=d-c=t＞0，得

ad-bc=（b-t）（c+t）-bc=（b-c）t-t2，

因b-c＜0，故ad-bc＜0，即ad＜bc，

故原不等式成立.

證法4：由a+d=b+c平方得a2+2ad+d2=b2+2bc+c2，

（a2+d2）-（b2+c2）=（a+b）（a-b）+（d+c）（d-c）

由題設知a-b=c-d＜0，a+b-d-c=（a-c）+（b-d）＜0，

故（a2+d2）-（b2+c2）=（a-b）（a+b-d-c）＞0，

2（bc-ad）=（a2+d2）-（b2+c2）＞0，即ad＜bc，故原不等式成立.

證法 5：同證法 1，即證ad＜bc，令a+d=b+c=2k，a=kt1，d=k+t1，

b=k-t2，c=k+t2，由a＜b＜c＜d知t1＞t2＞0，

ad=k2-2-，故原不等式成立.

證法 6：同證法 1，即證ad＜bc，由于 0＜a＜b＜c＜d，故只

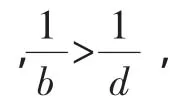
故原不等式成立.

三、拓寬思維途徑，深化結論形式

猜想1的六種證法都是從欲證不等式的結構特征出發，通過變更形式，并結合分子有理化、平方作差、引參換元等手段使問題得證，體現了數學轉化思想的重要作用.但六種方法有一個共同特點，即它們都得益于條件等式a+d=b+c的有效應用.因此，數學問題的求解與論證中，條件的運用是至關重要的.深入剖析等式a+d=b+c形式，它與等差數列有著內在的聯系，由此可得到如下的猜想：

注意到等差數列{an}中，當m+n=k+l時am+an=ak+al成立，故只需證

設等差數列{an}的首項為a1＞0，公差為d≠0.

法 1：aman-akal=［a1+（m-1）d］·［a1+（n-1）d］-［a1+（k-1）d］·［a1+（l-1）d］=［（m+n-2）-（k+l-2）］a1d+［（m-1）（n-1）-（k-1）（l-1）］d2.

因為m+n=k+l，所以由猜想1證法2知mn＜kl，

所以am an-akal=（mn-kl）d2＜0，所以am an＜ak al，

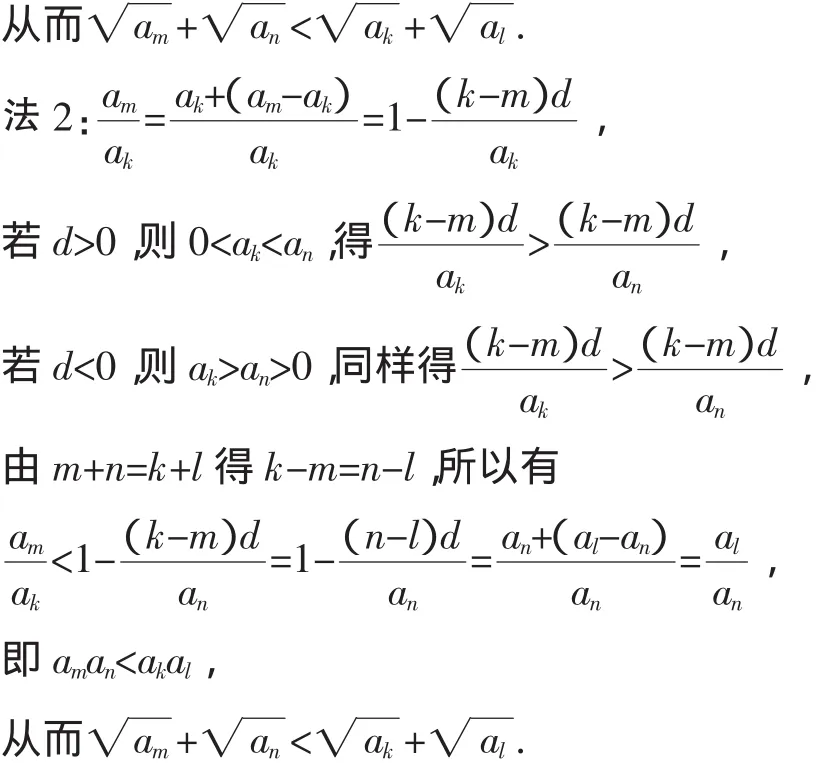
若改等差數列為等比數列，通過類比我們又可得到：

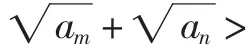
注意到等比數列{an}中，當m+n=k+l時aman=akal成立，故只需證am+an＞ak+al.

設等比數列{an}的首項為a1＞0、公比為q＞0，且q≠1.

由m+n=k+l知n-l=k-m，故有

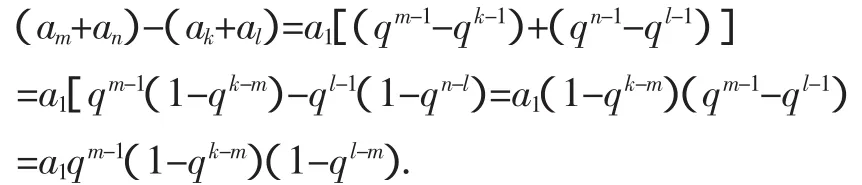
若q＞1，則由k-m＞0，l-m＞0 得qk-m＞1，ql-m＞1，從而（1-qk-m）（1-ql-m）＞0；

若 0＜q＜1，同理可得（1-qk-m）（1-ql-m）＞0，

所以am+an＞ak+al，

若深入思考，類比聯想，可進一步探究等差、等比數列的前n項和，得到：

猜想4：設{an}是正項等差數列，公差不為零，其前n項和為Sn.若正整數m，k，l，n滿足：m+n=k+l且m＜k＜l＜n，則Sm Sn＜SkSl.

證明：由等差數列的求和公式知要證SmSn＜SkSl，

即證mn（a1+am）（a1+an）＜kl（a1+ak）（a1+al）.

因為m+n=k+l且m＜k＜l＜n，

所以由猜想1的證法2可知mn＜kl，只需證

（a1+am）（a1+an）＜（a1+ak）（a1+al）.

又因為am+an=ak+al且aman＜akal，

所以（a1+am）（a1+an）-（a1+ak）（a1+al）=am an-akal＜0，

由此可知SmSn＜SkSl成立.

猜想5：設{an}是正項等比數列，公比不為1，其前n項和為Sn.若正整數m，k，l，n滿足：m+n=k+l且m＜k＜l＜n，則Sm Sn＜SkSl.

證明：由等比數列的求和公式得

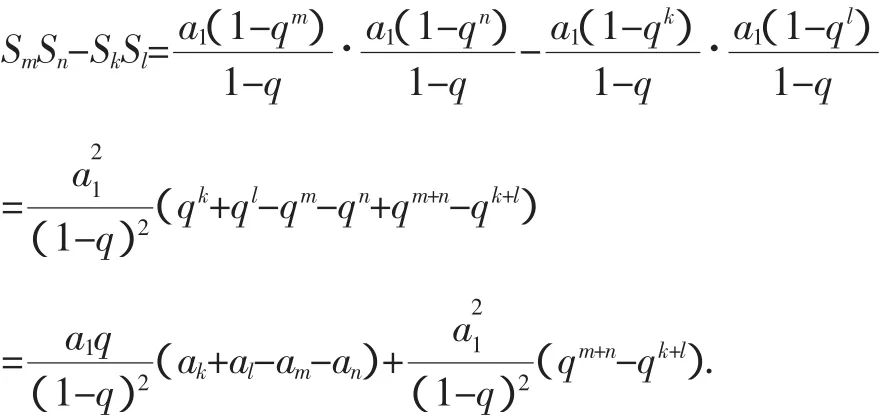
因為m+n=k+l且m＜k＜l＜n，

所以由猜想 3 知am+an＞ak+al且qm+n=qk+l，

從而有SmSn-SkSl＜0，即SmSn＜SkSl.

現行高中數學教材在“以人為本”這一新課程核心理念的引領下，為學生創設了多元化、多層次、有梯度、有意義的選擇資源，也為教者增添了擴充拓展、變式出彩的教學空間，因此教材中具有豐富的可供變式探究、拓展深化的素材，在數學課堂教學中，我們應充分運用這些素材，有針對性地引導學生開展自主探索，通過一題多解達到追求簡潔結果、優化解法的目的，通過一題多變達到舉一反三、觸類旁通、促進良好遷移之功效.