一道2013年安徽解幾高考題的推廣及背景

☉安徽省樅陽縣會宮中學 王懷明 汪玉生

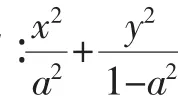
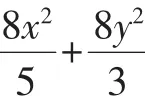
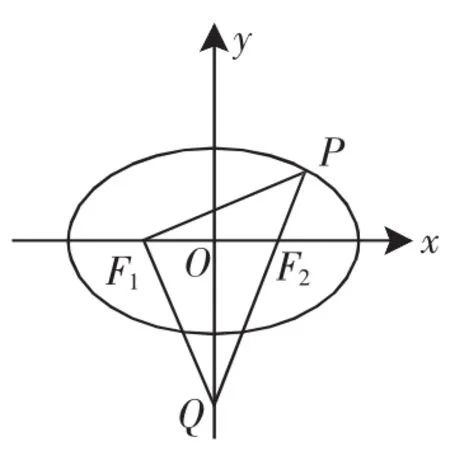
圖1

一、試題推廣

該題的長半軸與短半軸的平方和為a2+1-a2=1是定值，當長半軸的長度變化時，點P在定直線x+y=1上.那么對于任意橢圓，滿足條件的動點P是否在定直線上？經過探究，得到如下結論：

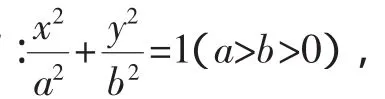
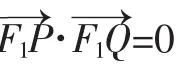
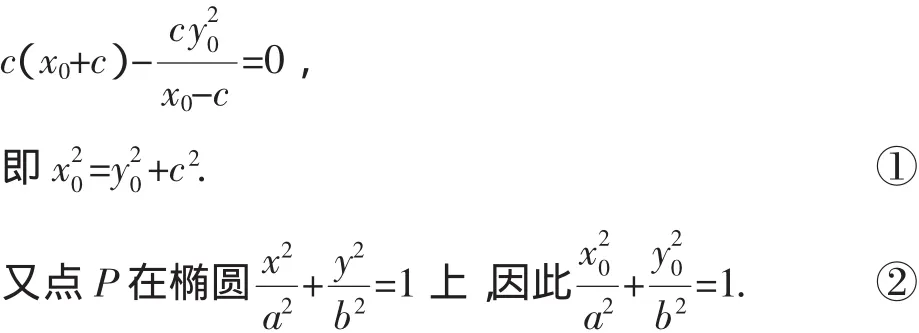
若點P在其他象限，也有類似結論，這里不贅述.類比橢圓，在雙曲線中是否也有類似結論呢？經過探究，得到如下結論：

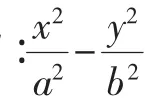
證明類似結論1，略.

二、背景分析

問題探究到此似乎應告一段落，但憑直覺，我們覺得對這個問題探討還不夠，認識還不深刻.安徽省近幾年解幾高考題都與切點、切線有關，而結論1和結論2中的兩條直線恰好是曲線在點P處的切線.為了說明這道高考題與以前的高考題以及圓錐曲線切點、切線之間的關系，下面以橢圓為例，先介紹有關知識.

1.圓錐曲線切點、切線的部分性質

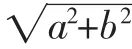
若改變條件和結論的順序，得到

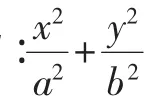
限于篇幅，以上性質的證明從略.

2.試題背景

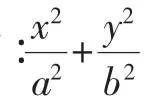
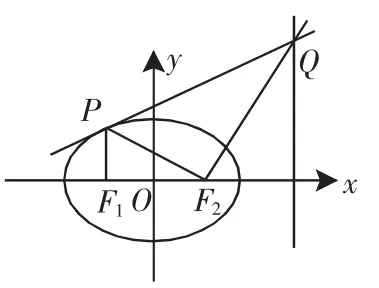
圖2

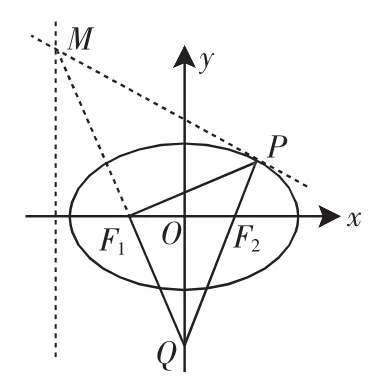
圖3

（1）若點Q的坐標為（4，4）；求橢圓C的方程；

（2）證明：直線PQ與橢圓C只有一個交點.

這道高考題的一般情形即為1中的性質②.我們再來看2013年的高考題（如圖3），若延長QF1交橢圓左準線于點M，則條件F1P⊥F1Q相當于F1M⊥F1Q.這道題相當于：

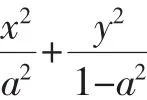
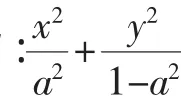
當然，還可以換成其他的敘述方式，這里不再一一列舉，同樣的，結論1和結論2也有多種敘述方式.無論怎樣的敘述，都能求得2013年高考題中點P的坐標為（a2，1-a2）.當然，這道題增加了一點難度，“證明：當a變化時，點P在某定直線上”.

通過對高考題分析發現，這道高考題保持了安徽省前五年解析幾何解答題的命題特色，即以“切點（極點）”、“切線（極線）”為背景，用初等數學知識方法解決具有高等數學背景的試題.可以預測，今后的安徽解析幾何解答題很有可能變換角度繼續考查與“切點（極點）”、“切線（極線）”有關的知識，希望引起大家的重視.這啟示我們，在高考復習中要反對搞題海戰術，要充分發揮高考試題的指導價值，選取有代表性的試題，深入研究，舉一反三，觸類旁通，理解本質，以不變應萬變.同時，這些試題又具有高等數學知識背景，試題之間也存在著緊密的聯系.作為教師，只有具備扎實的高等數學知識，才能高屋建瓴，研究命題思路，把握命題規律，注重通性通法.

1.方章慧，王懷明.一道解析幾何高考題的推廣及背景［J］.數學通訊（下半月），2012（12）.

2.梅向明，等.高等幾何［M］.北京：高等教育出版社，2000.

3.李文林.數學史教程［M］.北京：高等教育出版社，2000.