一道浙江競賽題證法的補充與引申

☉浙江省湖州市教科研中心 王勇強

☉浙江省湖州第五高級中學 計惠方

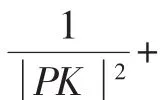
一、原證重現 彰顯通法 出現紕漏

1.原證：設K（a，0），過點K的直線方程為y=k（x-a），交拋物線于A（x1，y1），B（x2，y2）.

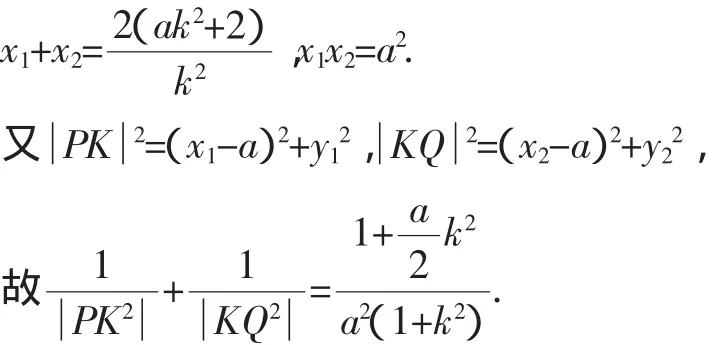
2.紕漏：過定點A（a，0）的直線y=k（x-a）中，不包含斜率不存在的直線，故必須單獨討論或驗證斜率不存在的情況.

二、證明補充 回歸一般 補充證法

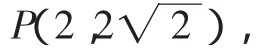
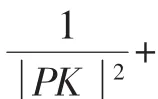
3.補充證法.

分析1：由于直線PQ的斜率可以不存在但不為零，為避免對斜率討論，一般宜設直線為x=ky+m.

證法1：設直線PQ的方程為x=ky+m，P（x1，y1），Q（x2，y2）.

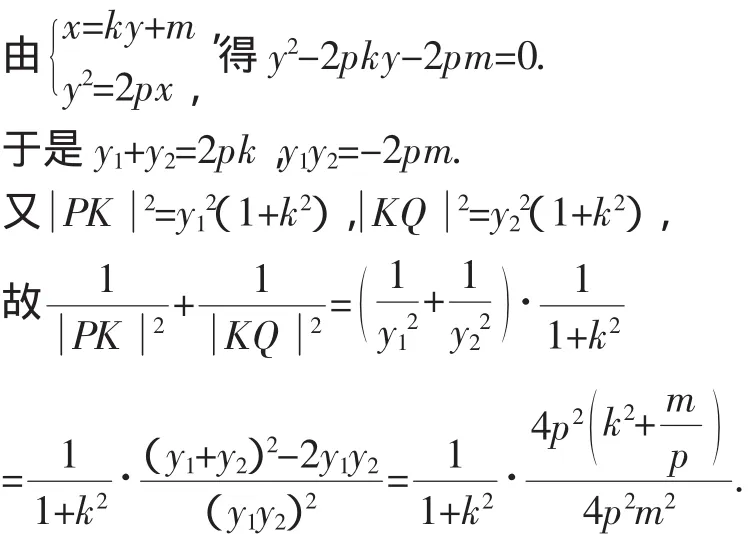
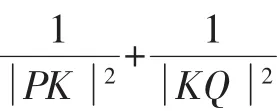
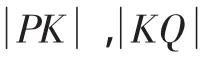
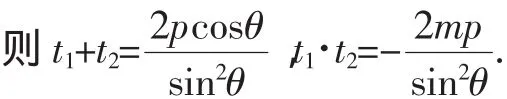
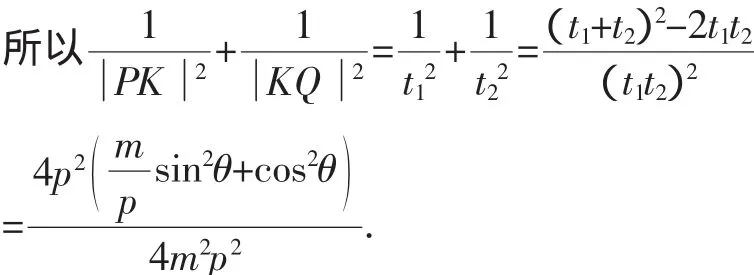
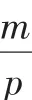
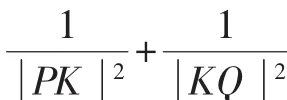
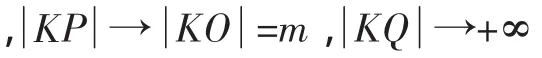
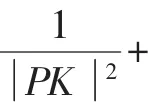
證法3：設直線PQ的方程為x=ky+p，P（x1，y1），Q（x2，y2）.

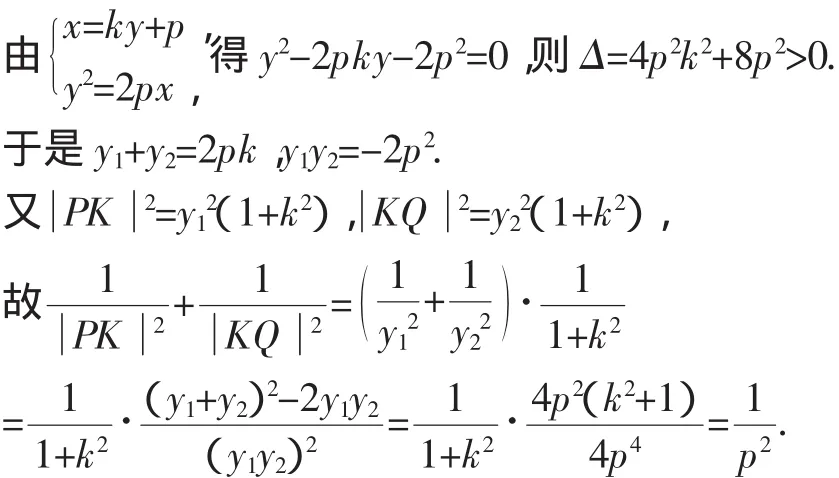
故存在唯一一點K（p，0），

三、先猜后證 引申變化 統一性質

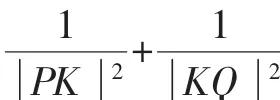
則當PQ垂直于x軸時，設P（m，n），則Q（m，-n），

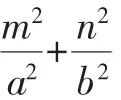
當弦PQ與x軸重合時，

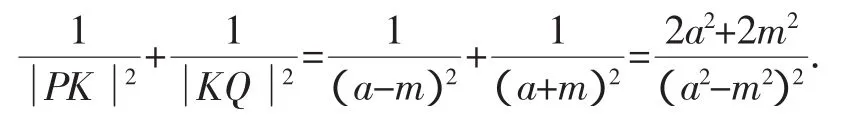
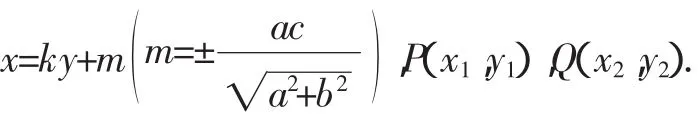
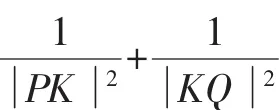
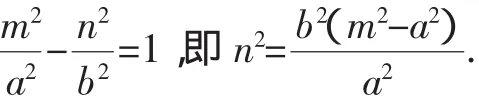
當弦PQ與x軸重合時，

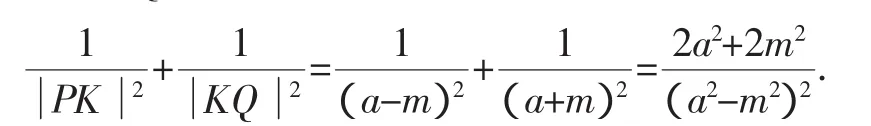
證明由讀者完成.