多元問題 “減元”處理——一道多元函數最值問題的多解及反思

☉湖南省衡陽縣職業中專 龍向東

學習數學的最終目的之一就是能夠用所學的數學知識解決問題.重視從不同的角度認識題目，并能夠充分揭示題目中蘊涵的信息，并從中獲得不同的解法，這無疑對培養學生思維的廣度、深度與靈活性，培養學生的創新精神，訓練發散思維，進而對學生綜合解題能力的提升起著重要的作用.

一、問題提出

已知x，y，z∈R，且x+y+z=1，x2+y2+z2=3，則xyz的最大值為______.

本題（源自2011年全國高中數學聯賽B，T9，原題：已知實數x，y，z滿足：x≥y≥z，x+y+z=1，x2+y2+z2=3，求實數x的取值范圍）條件簡潔明了，結構對稱優美，題意清晰而又內涵豐富.

二、解法探究

則①2-②，得2xy=（1-z）2-3+z2=2z2-2z-2，（*）

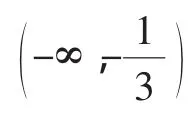
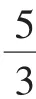
當且僅當x=y時取到等號.

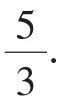
評注：目標式中有三個元，故從化歸轉化的角度看，減元轉化為單元函數的值域問題是方向，減元的技巧則是通過x+y與x2+y2的結構差異聯想到可用z來表示xy，另一個問題是如何準確界定z的范圍？解法1是通過（*）和②兩式結構特征聯想到它們之間隱含的均值不等式，從而得到關于z的另一個不等式.

解法2：由題意，將z=1-（x+y）代入x2+y2+z2=3，得

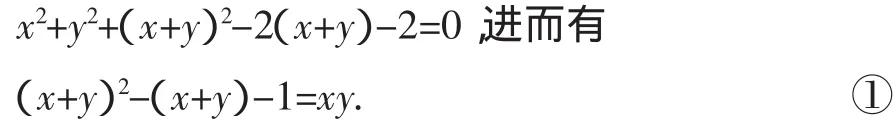
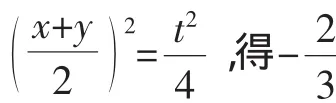
評注：本解法與解法1異曲同工，由于觀察的角度不同，所采取的換元思路是不一樣的，本法是用x，y表示z，再根據x+y與x2+y2的結構特征，用x+y整體表示xyz，而對于新元的范圍界定仍是通過不等式獲得，需要指明的是此類范圍限定中，往往需結合利用到兩個條件式的不等式才能獲得最終的范圍.

事實上，還有學生是這樣減元的：1=（x+y+z）2=x2+y2+z2+2（xy+yz+xz）=3+2xy+z（x+y），從而xy=-1-z（1-z）=z2-z-1，下同解法1.盡管過程未必簡潔，但卻透露重要的一點：至少學生發現了可以利用所學知識之間的結構特征聯系尋求解題的突破口，比如學生因為發現（x+y+z）2的展開式中含有xy，所以以此為開端逐步達到目的.G.波利亞在《怎樣解題》一書中這樣表述：“你應該考慮它，如果它看上去很有利，你應該考慮得更久一些；如果它看上去很可靠，你就應該弄清楚它能引導你到多遠，由于這個有用的念頭，整個情況已經發生了變化并從不同的方面重新考慮新的情況，尋找你與過去所獲知識之間的聯系.”或許有這方面的意思吧，教學中可以從題目的特點、條件結構等方面去指導學生解題.而對于解法1中函數f（z）=xyz=z3-z2-z中自變量z的范圍界定，還可以利用條件的結構特征求解.

解法3：由解法1可得

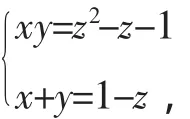
評注：通過x+y，xy與二次函數中根與系數關系式的結構相似性獲得構造的靈感，找到了突破口，可謂巧妙.類似地還可以采用解法4.

評注：此法從條件式本身的方程結構上聯想挖掘出了幾何圖形：直線與圓，結合題意轉化為相關解析幾何知識求解，巧妙的得到了范圍，其獨特的視角讓人叫好.

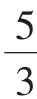
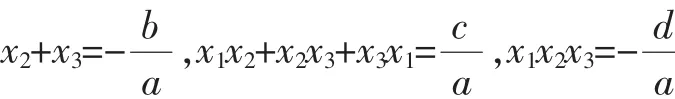
當然，就本題而言，從條件的結構特征角度觀察，是否還可以轉化為空間直角坐標系下平面x+y+z=1與球面x2+y2+z2=3有關的問題來求解，其中xyz是否可以理解為立方體的體積？是否可以通過選修教材中的球坐標方程來求解？是否還有其他的解法？這些都值得進一步研究.

三、反思

上述解法，體現了化歸思想的運用.化歸轉化思想是指運用某種手段或方法把待解決的較為生疏或較為復雜的問題轉化歸結為熟悉的規范性問題來解決的思想方法.化歸轉化思想是考生解決難題時常用的手段，也是高中數學思想方法的重要內容.在解題實踐中，大部分試題的條件與目標的聯系不明顯，能否根據問題的特點、條件與結論的結構和解題中出現的具體情況“隨機應變”，調整思路、轉換策略，是我們能否順利解題的一個關鍵因素，也是思維靈活性的一個重要體現，強化解題過程中的應變能力，有利于提高解決數學問題的思維能力.數學的符號化、形式化特征，為化歸思想的使用提供了便利條件，因為數學的符號語言具有演算性、形式化、符號化的特點，較易找到化歸的目標和方向.所以教學中：一方面，應該重視在化歸轉化思想指導下啟發引導學生從題目條件、結論的結構特征上去尋求解法，高中解題活動中經常能用到這樣的結構轉化，但如何能做到這樣的聯想呢？“其一能識別結構，特別是特征明顯的結構；其二能建立知識的框架體系，在這個體系下熟悉知識間的聯系、轉化、遷移、發展等，建立函數、不等式、方程的聯系，建立向量、幾何、代數、三角的聯系，建立求函數最值的模型結構與匹配的方法間的聯系等”；另一方面，應該鼓勵學生多角度、全方位地深入探索，“一題多解”作為訓練學生的發散性思維、培養和提高學生思維能力是一種很好的方法.另外還應注重解題后的反思歸納并注意突出通性通法，主要從解題結果、解題過程（對已有解法的回顧，包括計算是否正確，推理是否合乎邏輯，思維是否縝密等；探討解法的多樣性）、解題思想方法、習題特點等方面引導學生歸納反思，反思是學生提高解題能力的重要手段，本題解法較多，主要有基本不等式法和函數轉化法，這些方法將函數、三角、不等式乃至幾何的相關知識有機地聯系起來，這對于完善數學認知結構、提高思維的靈活性以及解題能力有著重要的意義.進一步地可從問題的結構特點、解題的思路和途徑等多種角度引導學生去觀察、感悟、聯想、歸納，要多問：解法結果有無問題？過程是否完整？哪種解法更簡單？哪種解法更常規，更巧妙，更典型？各解法的特點如何？阻礙解題的難點在哪里？能將上述解法分類么？解法中還涉及哪些知識？是否可以體會到解法中隱含的數學思想？

1.邊欣.一道2011年全國高中數學聯賽試題的簡解［J］.數學通訊，2012（2）.

2.沈良.略談數學結構觀下的解題與教學［J］.數學通訊，2012（12）.