創設概率背景 凸顯命題立意

☉江蘇省濱海中學 徐君華

瀏覽近年來高考試卷，不難發現概率統計題也融入新課標的教育理念，多角度、多視點地考查學生的數學素養，使學生的自主性和個性得以發揮，體現數學與社會、人與自然的和諧統一.許多試題體現了時代氣息，有創新特色.下面以2013年部分省市概率考題為例簡析如下.

一、關注熱點，聯系實際，極富時代氣息

例1 （2013年北京理）如圖1是某市3月1日至14日的空氣質量指數趨勢圖，空氣質量指數小于100表示空氣質量優良，空氣質量指數大于200表示空氣重度污染，某人隨機選擇3月1日至3月13日中的某一天到達該市，并停留2天.

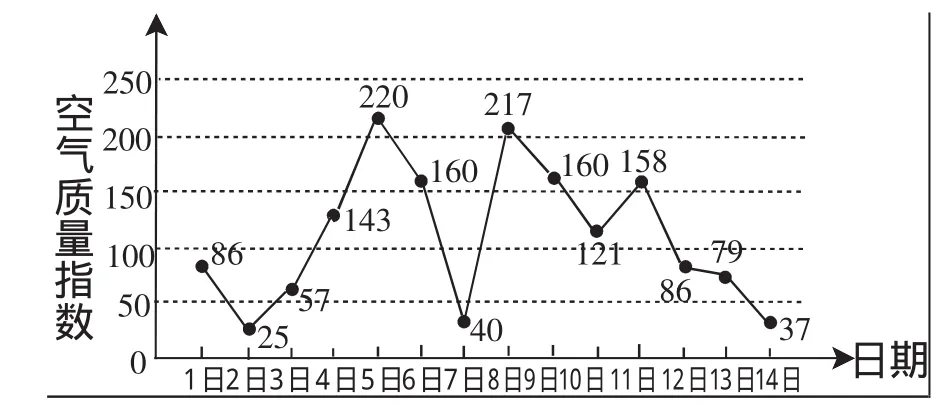
圖1

（1）求此人到達當日空氣重度污染的概率；

（2）設X是此人停留期間空氣質量優良的天數，求X的分布列與數學期望；

（3）由圖判斷從哪天開始連續三天的空氣質量指數方差最大？（結論不要求證明）

解析：設Ai表示事件“此人于3月i日到達該市”（i=1，2，…，13）.

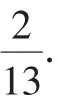
（2）由題意可知，X的所有可能值為 0，1，2，則

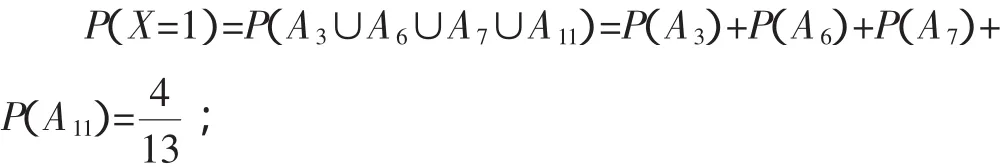
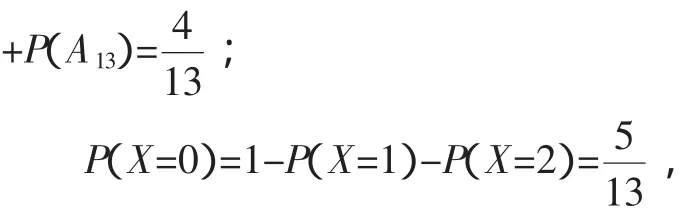
所以X的分布列為

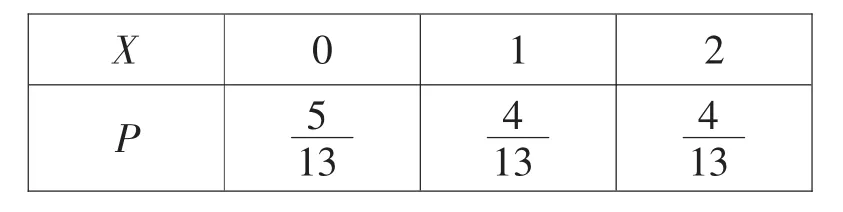
images/BZ_299_1402_1115_2187_1294.png

（3）從3月5日開始連續三天的空氣質量指數方差最大.

評析：該題直接關注當下的熱門“空氣質量”問題，引起了很多老師和學生的興趣，讓考生感到數學試題有了貼近生活的一面.它旨在教會學生學以致用，把知識運用到生活中.

二、代數幾何，交匯融合，命題立意深遠

近幾年的高考概率試題呈現出綜合性，如“概率與函數、不等式”、“概率與數列”、“概率與方程”、“概率與線性規劃”等相結合的應用題，也出現了與橫向學科相聯系的問題，體現了新課程的教育理念.

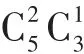
評析：本題以方程為依托，以排列組合和概率知識為工具，考查雙曲線的性質和分類討論思想，同時也對集合中的元素的分類進行了考查.

三、聯系生活，多向發散，意在創新能力

（1）若小明選擇方案甲抽獎，小紅選擇方案乙抽獎，記他們的累計得分為X，求X≤3的概率；

（2）若小明、小紅兩人都選擇方案甲或方案乙進行抽獎，問：他們選擇何種方案抽獎，累計的得分的數學期望較大？

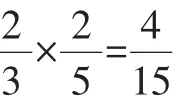
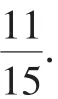
（Ⅱ）設小明、小紅都選擇方案甲抽獎中獎的次數為X1，都選擇方案乙抽獎中獎的次數為X2，則這兩人選擇方案甲抽獎累計得分的數學期望為E（2X1），選擇方案乙抽獎累計得分的數學期望為E（3X2）.

因為E（2X1）＞E（3X2），所以他們都在選擇方案甲進行抽獎時，累計得分的數學期望最大.

評析：本題是比較大小型試題，考查不放回的抽球、重點考查等可能事件、對立事件的概率，在知識應用上有一定的靈活性.

四、立足根本，回歸教材，展現命題理念

例4 （2013年湖北理）如圖2，將一個各面都涂了油漆的正方體，切割為125個同樣大小的小正方體，經過攪拌后，從中隨機取一個小正方體，記它的涂漆的面數為X，則X的均值E（）X=（ ）.

圖2

解析：X的可能取值為 0，1，2，3，分為以下情況：

當X=0 時，可看作切除“5×5×5正方體”的表面，得到一個“3×3×3 正方體”，故n（X=0）=3×3×3=27；當X=1時，一面涂色小正方體位于每個面的面心呈“3×3”分布，故n（X=1）=3×3×6=54；

當X=2時，兩面涂色小正方體位于每條棱上呈“3×1”分布，故n（X=2）=3×1×12=36；

當X=3時，兩面涂色小正方體位于每個頂點上呈“1×1”分布，故n（X=3）=1×1×8=8.

X的分布列為：

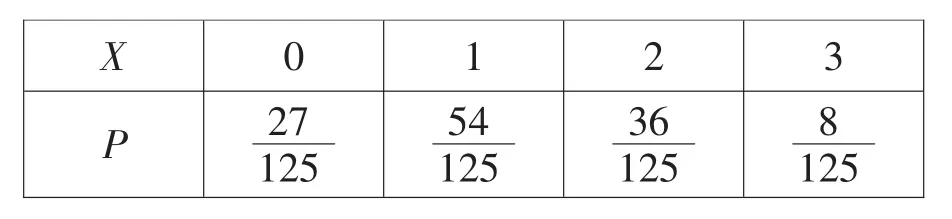
images/BZ_300_1397_1684_2298_1862.png

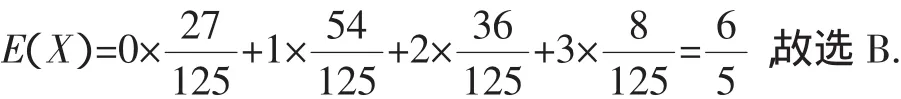
評析：本題源自人教A版必修2第36頁A組題9：一個紅色的棱長是4 cm的立方體，將其適當分割成棱長為1 cm小正方體，問：

（1）共得到多少個棱長為1 cm的小正方體？

（2）三面涂色的小正方體有多少個？表面積之和為多少？

（3）二面涂色的小正方體有多少個？表面積之和為多少？

（4）一面涂色的小正方體有多少個？表面積之和為多少？

（5）六個面都沒有涂色的小正方體有多少個？表面積之和為多少？

試題源于課本，高于課本.綜合考查了空間幾何體、古典概型和離散型隨機變量的分布列等知識，很好地整合了代數與幾何的交匯融合，立意深遠，有一定的區分度，屬中等難度題.

總之，近年來，以離散型隨機變量為平臺，以實際應用為背景，已經成為高考的熱點問題.這樣既能考查概率統計的核心內容和方法，又能考查綜合運用所學知識分析問題和解決問題的能力.