競賽中代數式求值的九種常用方法

☉江蘇省揚州市江都區實驗初級中學 李芳菲

在近幾年全國各地初中數學競賽中經常出現代數式的求值問題，這類問題涉及的知識面廣，技巧性強，方法靈活多樣，倍受命題者的青睞．解決這類問題的關鍵是理清已知條件與所求代數式之間的關系，然后選擇適當的方法求解．筆者結合近幾年各類競賽試題，歸納總結出解決這類問題的幾種常用方法，供讀者參考．

一、直接代入法

直接代入法就是將已知字母的值直接代入所求值的代數式中，通過化簡求得代數式值的方法．

點評：直接代入法是代數式求值中常用的方法之一，若已知代數式中所含字母的值，且直接代入后易求值時，可考慮利用直接代入法求解.

二、參數法

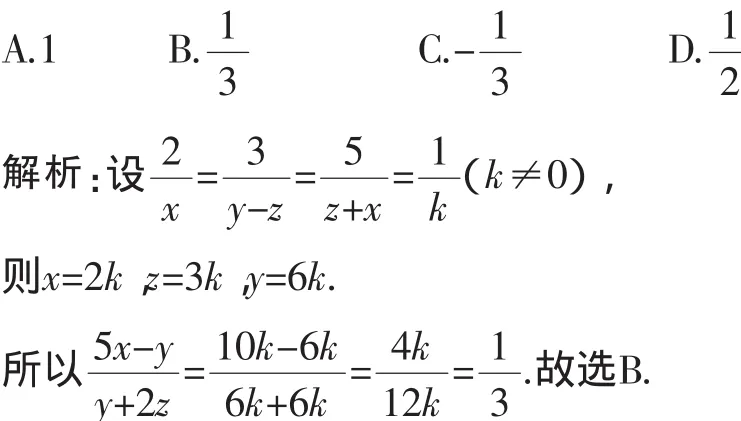
點評：參數法是解決這類問題的有效方法之一，利用這種方法求代數式值的關鍵是根據已知設出合理的參數．本題還可將x看作常數，然后用含有x的代數式表示y、z，直接代入所求值的代數式中化簡求值即可，但這種方法運算量比較大，沒有參數法簡便快捷．

三、整體代換法

若已知代數式中所含字母的值，但直接代入后不易求值時，可考慮利用整體代換法求解.

所以3a3+12a2-6a-12=3a（a2+2a）+6a2-6a-12=6a2+12a-12=6×6-12=24.故選A.

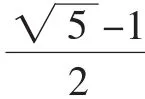
點評：整體代換法是解決這類問題最有效的方法，利用整體代換法求代數式值的關鍵是對已知條件和所求值的代數式進行適當的變形，然后整體代入求值即可．

四、利用非負數的性質

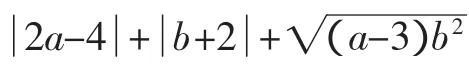
A.-1 B.0 C.1 D.2

解析：由二次根式中被開方數的非負性可知，（a-3）b2≥0，即a≥3.

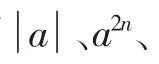
五、利用一元二次方程根與系數的關系

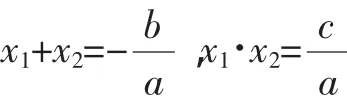
A.5 B.7 C.9 D.11

解析：由已知a2+1=3a，b2+1=3b，且a≠b，則a、b可以看作一元二次方程x2-3x+1=0的兩個實數根.由一元二次方程根與系數的關系，知a+b=3，ab=1.

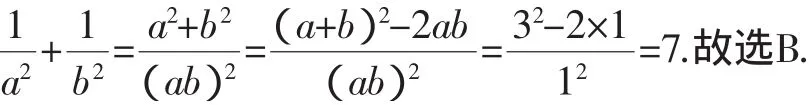
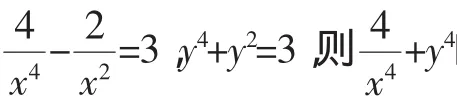
點評：利用一元二次方程根與系數的關系解決這類問題的關鍵是根據已知條件找出合理的一元二次方程，然后利用一元二次方程根與系數的關系列出相關字母之間的關系，再整體代入所求值的代數式中化簡求值即可.若直接根據已知條件求出相關字母的值直接代入所求值的代數式中，運算量會非常大，而且容易出錯.

六、利用方程組

例9（“《數學周報》杯”2010年全國初中數學競賽）若x2+xy-2y=1，y2+xy-2x=1，則x+y的值為______.

由①+②可得，x2+2xy+y2-2（x+y）=2，

即（x+y）2-2（x+y）-2=0.

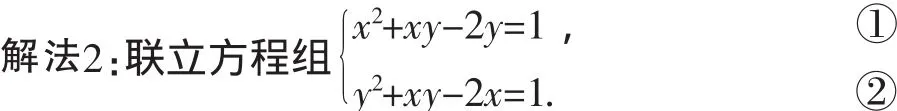
由①-②可得，x2-y2+2（x-y）=0，即（x-y）（x+y+2）=0.

所以x-y=0或x+y+2=0.

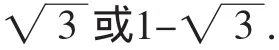
當x+y+2=0時，x+y=-2.由①知x（x+y）-2y=1，從而-2x-2y=1，即-2（x+y）=1，將x+y=-2代入得，-2×（-2）=1，這是不可能的，故x+y+2≠0.

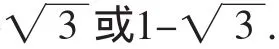
七、利用折項相消法

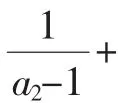
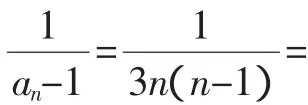
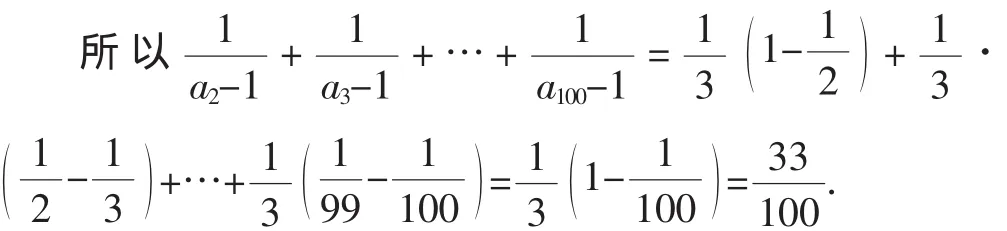
八、利用整體設元法

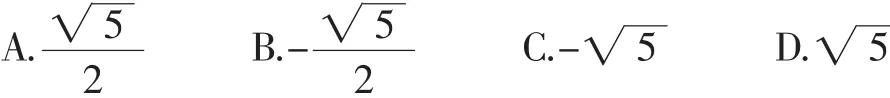
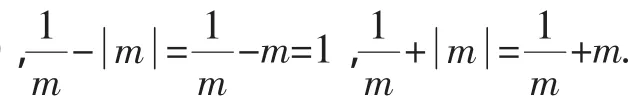
九、利用主元法

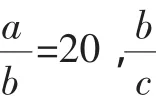
解析：以c為主元，則b=10c，a=20b=200c.

點評：當已知條件和所求值的代數式中字母較多時，可選定其中一個字母為主元，然后用這一主元的代數式表示其他字母，最后代入所求值的代數式中化簡約分，即可求得代數式的值．