“放”得妙解紛呈，“收”得精彩無限——例談一題多解教學中的“收”“放”策略

☉江蘇省連云港市新壩中學 周 楊 喬華利

“一題多解”是數學學習道路上最為絢麗的一道風景.就教學價值而言，我們可以利用問題解法的開放性，在發散思維（“放”）與聚合思維（“收”）的結合訓練中優化學生的思維品質，在對解法進行多角度的對比和優化中發展學生的元認知能力，在促進學生認知能力發展的同時，使學生的知識結構得到完善.

那么實際教學中，怎樣的“收”、“放”操作，才能讓“一題多解”的上述教學價值得到有效挖掘和充分體現呢？筆者在此結合一道例題的教學談談自己的一些淺見，與同行交流.

一、例題及簡析

圖1

簡析：本題作為一道填空題，通常會被認為是一道“小題”.然而筆者認為，本題雖然題設簡單，卻有一定的思維含量.初中階段學生對“圓”的認識限于“形”，對涉及坐標的直線問題多用“數”，本題將圓放入平面直角坐標系內，以點的坐標作為問題指向，題設中又暗含較多的特殊角，這使得問題體現出一定的綜合性的同時，“入口”也變得比較開放，學生可以利用多種知識和方法來切入問題.另外，本題的難度與思維含量合適，既能給學生一定的問題空間，又容易在教學中取得較廣的調動面.這些都決定了對本題的教學有必要“小題大做”！

二、教學中的“收”與“放”

1.在“百花爭艷”的“放”中顯化思想方法

每一個問題的解決過程中都悄悄地流淌著思想方法的潛流，教師的一個重要工作就是讓這些思想方法清晰起來，明亮起來.有一種觀點認為，數學思想方法在教學中應當多“意會”而不必“言傳”.筆者認同這一點，但我們也應當承認的是，在教學實踐中，特別是在具體問題解決的教學過程中，盡量讓數學思想方法顯化也是相當必要的.所謂“顯化”，不是把數學思想方法空洞地掛在嘴上，而是指在具體的問題解決過程中將不同的思想方法具體化為不同的解題思路，再將不同的解題思路以具體的解答過程呈現出來.顯然，如果能在同一個題目中對不同思想方法進行具體化呈現，帶來的“顯化”效果是更為突出的！

解法1（解析法）：如圖2，設Rt△AOB的斜邊AB的中點為M，則M是△AOB外接圓的圓心.

連接PM并延長交x軸于N點.

圖2

直線OP的解析式為y=x.

因為P點是直線OP與MN的交點，所以列方程組：

解法2（解直角三角形法一）：設Rt△AOB的斜邊AB的中點為M，則M是△AOB外接圓的圓心.

圖3

于是∠OPM=∠MOP=∠AOP-∠AOM=45°-30°=15°，OM=PM=2.

延長PM，作OT⊥PM，垂足為T，則∠OMT=30°.

過P作PH⊥x軸，垂足為H.

解法3（解直角三角形法二）：如圖4，作BS⊥OP，PH⊥x軸，垂足分別為S、H，連接PB.

因為∠AOP=45°，所以△BOS是等腰直角三角形.

圖4

所以∠BPS=∠BAO=30°.

解法4（構造方程法）：如圖5，連接PB、PA，作PH⊥x軸，垂足為H.

因為∠ABP=∠AOP=45°，AB是直徑，所以△PAB是等腰直角三角形.

圖5

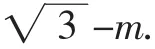
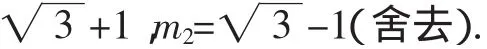
如圖6，連接PM、OM，作PH⊥x軸，垂足為H，作MR⊥PH，MT⊥OA，垂足分別為R、T.

圖6

在Rt△POH中，∠AOP=45°，則∠MOP=∠MPO=15°，則∠MPR=∠MOT=30°.

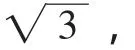
連接PM并延長交x軸于N點（如圖7）.

因為∠AOP=45°，所以∠AMP=90°.

所以△AMN∽△PHN∽△AOB.

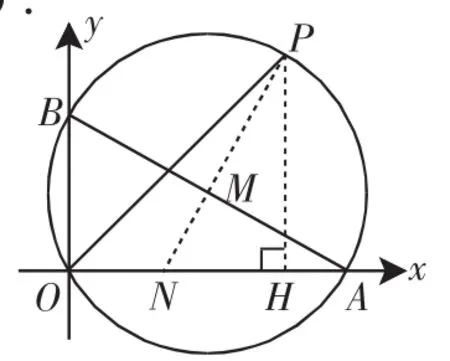
圖7

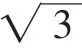
易得PH=OH.

解法7（全等變換法）：如圖8，作PQ⊥y軸、PH⊥x軸，垂足分別為Q、H，連接PB、PA.

因為OP是∠AOB的平分線，所以PH=PQ，四邊形OHPQ是正方形.

由∠AOB=90°，可得AB是圓的直徑.

又因為∠ABP=∠AOP=45°，所以△PAB是等腰直角三角形，PA=PB.

所以Rt△PQB≌Rt△PHA（HL）.

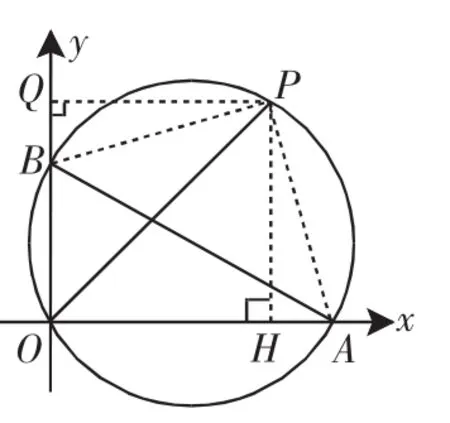
圖8

則有HA=BQ.

解法8（相交弦法）：如圖9，設OP與AB的交點為T，作TN⊥OA，PH⊥OA，垂足分別為N、H.

圖9

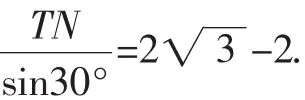
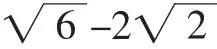
需要指出的是，在解法的教學呈現中，我們不應簡單地求“多”，而應當讓“多解”體現在不同的數學思想方法的運用，或者是解決方法體現不同的角度和高度.就本題而言，解法1作為“解析法”，體現的更多的是數形結合思想；解法2與解法3將問題轉化為求線段的長，然后利用角度的特殊性將問題再轉化為解直角三角形問題，體現的是化歸與建構模型的思想；解法4設立未知數，將未知量構造到一個直角三角形中，運用勾股定理列方程，體現了方程思想的運用；解法5通過構造三角形全等轉化未知量，體現了等量轉化的思想；解法6和解法7分別運用了構造相似圖形和全等圖形，體現了幾何變換的思想……當這些方法呈現在一起的時候，學生不僅看到了“百花爭艷”的精彩，更真真切切地感受到每一種思想方法的具體存在與運用，對于初中生來說，在一個問題上呈現多種思想方法，就像一個植株上開出了多色的花來！這種對比是鮮明的，這種印象是深刻的，這種體驗是無可替代的.

2.在集思廣益的“放”中實現廣泛的思維調動

數學課堂的一個永恒追求是廣泛的思維調動.相對于那些解法封閉的問題，多解問題往往往更容易調動學生的積極性.以本題為例，筆者在一次階段測驗中選用它，測驗的結果并不如人意，全班50名學生中，僅有8名學生正確解答了本題.在試卷講評時，筆者發現8名學生中有4名學生采用解法1，有2名學生采用解法2；另兩名學生分別采取全等變換法和構造方程的方法.幾位同學的解法呈現之后，立即激發了其他同學對試題進行再思考.一段時間之后，各種新解法如雨后春筍般“冒”了出來.比如，當一名同學向大家講解構造全等的方法之后，很快就有同學想到通過相似變換的方法，緊隨其后，幾種巧妙利用特殊角的方法就被其他同學想到，一時間，課堂上人人都參與進來，有人在相互交流；有人在獨自沉思；有人眉頭緊鎖；有人眉開眼笑……

其實很多時候，學生之間還會形成一種相互啟發的作用.就本題而言，大部分學生在考試的時候沒能解決問題，但他們往往對問題都有了較多的思考，他們往往就是在某一個關鍵處受阻，一個節點沒能打通.在課堂上，當某一位同學用一種方法擊破這個節點的時候，往往能帶來很好的啟發作用，帶來一種“連鎖反應”.就像一個人驚喜地找到一個蘑菇的時候，其他人也就能很快地在它周圍的土下找到成堆的蘑菇！教師要做的就是通過有效的課堂組織，為學生創造這樣的課堂氛圍，努力在這種集思廣益的“生生互動”或“師生互動”中調動學生“挖出更多蘑菇”的積極性！比如說，解法3呈現之后，很快就有同學受其啟發而提出如下兩種新解法.

解法9：如圖10，作AS⊥OP，垂足為S，連接AP.

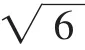
圖10

圖11

解法10：如圖11，作PH⊥x軸，垂足為H，設AB的中點為M，則M是圓心.連接PM，則∠AMP=90°，∠MPR=∠BAO=30°.

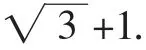
可以看出，上述兩種解法其實就是在“解法3”的啟發下，對“解直角三角形法”的再思考.筆者在實踐中發現，在諸如此類的“一題多解”問題的教學中，初中生較強的表現欲在互動探究的過程中表現得淋漓盡致，思維的調動既體現出了廣度，也體現出了深度.

3.在“殊途同歸”的“收”中完善認知結構

由一個問題的條件或事實出發，從各個方面思考，尋求多種解法.這樣的過程體現的是思維的發散性，一種思維的“放”；從各個方面去思考問題的過程中，多種方法最終要歸結到一個問題的有效解決，并且我們總是力求用最為簡捷有效的解決方法，這樣的過程又體現了思維的“收”，即是一種聚合思維.事實上，問題解決往往是依賴于發散思維與聚合思維的有機結合：一方面要能廣開思路，自由聯想，提出各種解決問題的設想與方法；另一方面，又要善于篩選解題方法，能選用一種最好的方案或辦法來解決問題.

就本題而言，首先應當引導學生認識到多角度獲解的可能性.比如，我們可以想到用解析法求兩條直線交點的坐標；我們可以想到圓中垂徑定理的運用；我們可能由OP的特殊位置（∠AOP=45°）想到構造全等變換；我們還可能由線段間特殊的位置關系想到構造相似變換；我們還可以由題中特殊角想到解直角三角形……這是讓思維盡可能地“放”，在這個“放”的基礎上，學生還應當認識到這些不同的方法能“殊途同歸”又體現了不同知識與方法之間存在著本質的關聯，比如全等與相似、方程與函數之間特殊與一般的關系；“數”與“形”本質上的統一.這樣的認識過程體現的是思維的“收”，“收”的過程，很大程度上就是不同知識溝通聯系的過程，是個體內部認知結構發生“順應”的過程.

4.在對比優化的“收”中發展元認知能力

即使在成功的解決問題之后，我們仍然需要思考：是否還有更為精致簡潔的方法，或者原本的方法中是否存在著某種迂回從而可以進一步簡化？這種思考方式是我們應當在數學教學過程中向學生不斷滲透的.如何讓學生產生這種努力尋求“最優化”的“心向”呢？筆者認為，解法對比就是一種最為有效的方法.我們容易發現，因為思維的慣性作用，個體對自己的解題過程往往很難作出有效的調整，而正是這種調整上的困難，使得我們在解決問題的時候陷入困境或者迷途難返.這也就是說，對自己的解題過程作出優化所需要的不僅僅是對問題的數學本質有更深的認識，更需要自我批判、自我反思、自我監控等元認知能力，而發展這種“元認知”能力的一個有效途徑就是將學生引入解法對比中.有對比才會感受到“優化”的存在，感受到“優化”才會有自我的反思，有自我反思才會有自我批判與自我監控能力的形成與發展.

本題的教學中，筆者發現正確解答本題的學生中采用解法1（解析法）的最多，其次是解法2，通過課后交流發現，最初想到用解法2（包括沒能成功的）的學生遠遠多于前者.隨著新方法不斷產生，我們很容易發現其實這兩種方法都顯得迂回煩瑣，于是有一個問題凸顯出來：為什么這兩種方法迂回煩瑣卻被很多學生采用呢？筆者研究發現，這兩種解題思路就其產生過程而言，都具有明顯的“合理性”.以解法2為例，欲求P點的坐標，很容易想到求出OP的長，而OP作為圓中的一條弦，學生容易想到利用垂徑定理；在構造出垂徑定理常用的直角三角形之后（圖3中的△MSP或△MOS），容易求出其中銳角（∠MPS或∠MOS）是15°，圓的半徑是2，于是問題歸結為能否利用這些條件求出直角邊（PS或OS）的長.但是，很多學生就是“堵”在這里了：他們不能找到合適的方法來利用這個15°角，試圖在垂徑定理的基礎上找到可利用的線段關系，也很難找到.從這個過程中我們容易發現，所謂解題思路的“合理性”，其實很大程度上又會表現為思維的定式作用，比如學生往往將“圓中求弦長”定式于垂徑定理.如果在陷入困境之后及時返回起點再分析，也就容易發現題中涉及45°、60°、30°等更為特殊的角，利用這些特殊角的三角函數來解直角三角形，就可能想到解法3.解法3就比解法2顯得更為簡捷，這一點，學生在解法對比時很容易感受到.筆者在課堂上發現，當一個學生在課堂上向大家呈現解法3的時候，有很多學生驚呼：“我怎么就沒想到呢！”同樣，當解法5呈現出來的時候，解法4因為解方程過程的煩瑣而黯然失色；當解法7巧妙地利用幾何變換思想與方程思想使問題輕松獲解時，全班同學一致叫好……這樣的對比過程中，學生不由自主地產生了這樣的感嘆與思考：原來思路可以這樣的開闊！我為什么就沒想到呢？顯然，這樣的感嘆與思考就是一種自我反思的具體表現.