勤提煉 活運用 促提高——“雙A”字基本圖形在解題中的應用

☉湖北省陽新縣白沙中學 羅 峻

☉湖北省陽新縣白沙中心校 馬先明

相似是初中幾何的核心模塊，是中考中的重要考點，也是考查學生分析問題和解決問題及綜合能力的重要載體．相似往往與三角形、四邊形、圓等幾何圖形結合，使問題的難度加大．要突破這一難點，不僅要牢固掌握三角形相似的基本判定、性質和相關定理，還需要借助豐富的圖形識別經驗．為此在平時教學中，我們要適當提煉一些基本圖形，并有意識地進行基本圖形專題方面的訓練，進行幾何基本圖形的識別和運用．下面結合近年的中考、競賽試題，提煉出相似問題中常見的“雙A”字圖形，讓我們體會基本圖形在解題中化隱為顯、化難為易的作用．

一、“雙A”字圖形及其基本結論

圖1

從上面基本圖形（圖1）的結構看，像兩個并排著的背靠背的英文字母“A”，我們暫且稱之為“雙A”字圖形.若熟悉上面基本圖形的結構特點，在平時學習中，對于幾何圖形比較復雜的試題，便能較快地分離出隱藏于其中的基本圖形，抓住問題的本質，從而快速解決問題.

二、直接運用基本圖形解題

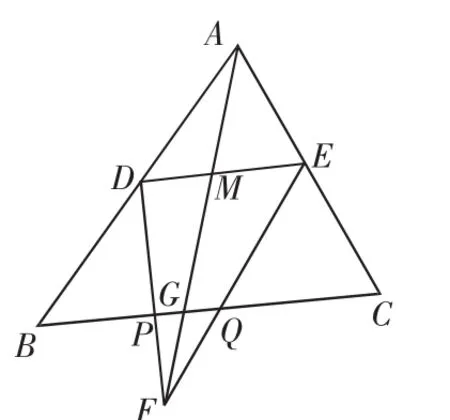
圖2

解析：所證的四條線段都在同一條直線上，無法直接運用相似的性質證明，可嘗試尋求過渡比實現解題．找出這四條線段所在的三角形，很快發現DM、ME與所證結論有關聯，且這六條線段存在于兩個“雙A”字圖形中，其中一個“雙A”字圖形是倒放著的．

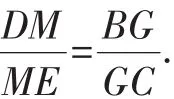
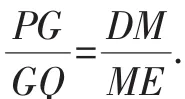
點評：根據所證結論并結合題設圖形的鮮明特征，找出其中隱藏著的“雙A”字圖形，運用該圖形的結論，得出比例式，利用過渡比便可快速證題.

例2（濟寧中考題）在一次數學課上，一位同學提出：“誰能幫我用一副沒有刻度的三角板找出線段AB的中點？”小華說：“我能做到，我的做法是，用這副三角板任作一條直線MN∥AB；在直線AB、MN的同側任取一點P，連接PA、PB，分別交直線MN于C、D；再連接AD、BC，相交于點E；畫射線PE交線段AB于點O，點O就是線段AB的中點.”你認為O是線段AB的中點嗎？說明理由.

解析：先按照題意畫出如圖3所示的圖形.

因為CD∥AB，結合“雙A”字圖形和結論（1），知：

圖3

點評：由兩條直線平行的條件可看出題設圖形中隱藏著的“雙A”字圖形，同時還隱藏著“8”字型的對頂三角形，這樣得出相關的比例線段，用過渡比實現證題．

例3 （武漢中考題）在△ABC中，∠BAC=90°，正方形DEFG的四個頂點在△ABC的邊上，連接AG、AF，分別交DE于M、N兩點.

（1）如圖4，若AB=AC=1，直接寫出MN的長；

圖4

（2）如圖5，求證：MN2=DM·EN.

圖5

又GF=DG=EF，即GF2=CF·BG.①

由DE∥BC，利用“雙A字”圖形及結論（1），知：

結合①和②，得MN2=DM·EN.

點評：本題是相似與三角形、四邊形相結合的綜合題，要運用相似的性質進行解題，而解題的關鍵在于運用基本圖形快速得出相關線段成比例.其中，第一問是“雙A”字基本圖形的直接應用；第二問除了“雙A”字圖形外，還蘊含有“兩角對應相等的三角形相似”的基本圖形，由相似的性質得出比例式，兩者有機結合，使問題易于解決.

從幾何圖形中直接分離出基本圖形，運用圖形的性質相對容易，而如何從幾何圖形中構造出基本圖形進行運用，是解題的難點所在.為此必須仔細觀察題目給予的圖形并研究圖形的結構特點，結合已知條件或所求、所證內容，產生豐富聯想，構造出能解決問題的基本圖形.

三、構造基本圖形解題

圖6

圖7

解析：（1）圖6中，由AB為直徑，AP為切線，易知AF⊥AB.又CD⊥AB，則CD∥AF.

在“8字”型的對頂三角形中，△ECF≌△EOB（SAS），因此∠FCE=∠EOB=90°，則直線CF是半圓O的切線.

（2）連接BC并延長交AP于點G，連接AC、CO（如圖7）.

由第一問的CD∥AF，CE=DE，利用“雙A”字圖形的結論（3），知FG=FA.

在Rt△ACG中，FC為斜邊AG的中線，因此FC=FA，則∠FCA=∠FAC.

又∠OCA=∠OAC，則∠FCO=∠FCA+∠OCA=∠FAC+∠OAC=∠FAO=90°，故FC是半圓O的切線.

點評：本題是一道探索性問題，第一問通過問題的特殊情形探究圖形的本質屬性，第二問從特殊化向一般情形拓廣，進一步探索結論的“不變性”．雖然能猜測結論不變，但求證它較難．此處由“CD∥AF”和“E為CD的中點”這兩個條件，聯想到構造出“雙A”字圖形，運用基本圖形的結論得出點F為AG的中點，再運用圓、直角三角形、等腰三角形的有關性質進行綜合運用．

例5 如圖8，在△ABC中，∠BAC=90°，AD⊥BC于D，P是AD的中點，BP的延長線交AC于E，EF⊥BC于F.求證：EF2=AE·EC．

解析：由已知條件AD⊥BC、EF⊥BC，知AD∥EF，延長FE交BA的延長線于點G，就可以構造出“雙A”字圖形．

由AD∥EF和AP=DP，利用結論（3），知EG=EF.

圖8

點評：根據條件“P是AD的中點”和AD∥EF，將圖形補全，便構造出“雙A”字圖形，再運用其性質可快速解題．可見，熟悉基本圖形的特征，是正確作出輔助線的前提．

例6（2003年全國數學競賽）如圖9，已知AB是⊙O的直徑，BC是⊙O的切線，OC平行于弦AD，過點D作DE⊥AB，垂足為E，連接AC，與DE交于點P，問：EP與PD是否相等？證明你的結論．

解析：由已知條件“AB是⊙O的直徑，BC是⊙O的切線”，易知：BC⊥AB.又DE⊥AB，所以DE∥BC．根據已有結果DE∥BC，以及圖形的結構特點，還有猜想的結論EP=PD，易聯想到“雙A”字基本圖形，由此延長AD、BC交于點F．

圖9

說明：本題是一道結論開放性問題，需用到兩個基本圖形：“雙A”字基本圖形和“單A”字基本圖形進行解題，難點在于作出合適的輔助線，這需要根據已知條件和所證結論逆向思考，產生聯想，讓看似并不存在的基本圖形顯露出來，產生作用．

四、綜合運用基本圖形解題

例7 如圖10，在△ABC中，BD=DC，O是AD上一點，BO、CO的延長線分別交AC、AB于F、E.求證：AD平分EF．

圖10

簡解：設AD與EF交于點G，過點A作BC的平行線，與CE、BF的延長線分別交于M、N．

點評：由已知條件和所證結論，猜測可能要用到本文中的基本圖形，但缺少平行線這個條件，故突破問題的關鍵在于證EF∥BC，為此過點A作BC的平行線，再運用相似的性質綜合解題．本題難度大，原因有三：一是構造“8”字型基本圖形；二是利用“雙A”字基本圖形的性質解題；三是圖10中出現多個基本圖形的疊加和隱藏.

在“雙A”字基本圖形中，由EF∥BC，BD=CD，運用結論（3），得EG=FG，即AD平分EF．

圖11

簡證：過點C作AB的平行線，交PA、PB的延長線于點F、G．

PA為⊙O的切線，由弦切角定理，知∠FAC＝∠ABC.

由AB∥CG，得∠BCG＝∠ABC.

因此∠FAC＝∠BCG.①

由切線長定理，知PA＝PB.又AB∥FG，則△PFG為等腰三角形，所以∠F＝∠G.②

點評：此題是一道頗有難度的競賽題，原解法運用相似三角形得出多個比例式，再將它們乘除運算，曲折迂回，不易思考．這里結合題設的圖形，構造出“雙A”字基本圖形，并利用結論（1）、相似三角形的性質和面積比進行證明，直觀明了，簡捷易懂．

例9（全國初中聯賽）如圖12，設凸四邊形ABCD的對角線AC與BD交于點M，過點M作AD的平行線分別與AB、CD交于點E、F，與BC的延長線交于點O，P是以O為圓心、OM為半徑的圓上一點.求證：∠OPF=∠OEP.

圖12

圖13

證明：如圖13，延長BC、AD交于點H.

又∠FOP=∠POE，利用“兩邊對應成比例且夾角相等的兩三角形相似”，得△OFP∽△OPE，因此對應角∠OPF=∠OEP．

五、教學反思

數學是關于數與形的科學，形是數學的重要表現形式，學習數學離不開對幾何圖形的研究．《數學課程標準》在幾何方面的學習要求是“能從較復雜的圖形中分解出基本的圖形，并能分析其中的基本元素及其關系，利用直觀來進行思考”．可見從復雜圖形中“離析”出基本圖形，是解決圖形問題必須具備的重要能力之一，也是解決幾何問題的重要方法．同時數學也是關于模式的科學，這反映在數學解題時，需要進行模式識別，需要構建標準的模型．當我們面對一個陌生的、看似復雜的幾何問題時，往往都可以將它轉化為已解決過的、較熟悉的、簡單的幾何圖形，這里用到的基本圖形就是解決問題的一個模式．用基本圖形來分析、解決問題，是解題的常用方法、通用方法，可以發揮數學教學的長期效益．因此，必須重視基本圖形在解題中的作用．

總體來說，數學中的基本圖形分為兩種：一種是教材中的定義、定理和性質所對應的圖形——單一型基本圖形，這些圖形一般都有與概念或定理的條件及結論的外形相呼應的結構特征，像直線、平行線、相交線、三角形、四邊形、點與圓、圓的切線、弦切角等都屬于單一型基本圖形；另一種基本圖形是例題和習題所對應的圖形——復合型基本圖形，它是單一型基本圖形內容的擴展與延伸，它常常把一些重要的、常用圖形加入到單一型基本圖形成為復合型基本圖形的一部分，一般而言復合型基本圖形都由兩個或兩個以上的單一型基本圖形組合而成，所蘊含的結論更豐富、實用性也比較強．比如：角平分線和平行線組合成為等腰三角形，一線三垂直（即在同一直線上，有三個直角）圖形可產生三角形全等或相似，圓的切線長基本圖形中蘊含有多對三角形全等、多對線段相等、多對角相等……復合型基本圖形在課本中以例題、習題的形式零散出現，我們應引導學生收集與歸納．

學生對于單一型基本圖形一般較熟悉，用的比較得心應手；而對于復合型基本圖形，雖然知道圖形與結論，但在解題時卻常常忽略它的存在，導致解題困難或失敗.為什么單獨把這些復合型基本圖形提出來，學生馬上就知道其結論，而解題時卻熟視無睹？這就要求我們在教學過程中，一方面應重視基礎知識、基本技能、基本方法的教學，注重對知識的發生、發展過程的揭示，因為定理、公式推證的過程就蘊含著重要的解題方法和規律，教師應該充分暴露思維過程，發掘其內在的規律.長此以往，學生便可以潛移默化，學會解決問題的思考方法.另一方面，注重對這些基本圖形的提煉并會靈活運用.要引導學生研究這些看似不起眼的復合型基本圖形，分析基本圖形的特征，歸納基本圖形的性質，深刻掌握基本圖形，理解基本圖形的性質都是以怎樣的方式發揮作用.

為此，在平時的教學中，應該培養學生對一些基本題型和基本圖形的敏銳觀察力，借給學生一雙“數學慧眼”.在每學習一部分課本內容后，可以嘗試以“專題講座”的教學模式，引導學生自主探索、自我總結、逐步提高，對課本的這部分例題、習題加以提煉并深刻研究，形成結論儲備起來，達到“見到圖形，想到性質；想到性質，想全圖形”的要求，在頭腦中形成系統完備的待用基本圖形庫，最終把基本圖形當作利刃，用到解題中去.

總之，引導學生提煉總結課本中的基本圖形，并運用基本圖形解題，不僅有助于激發學生的學習興趣，提高解題效率，而且對發展學生的數學思維能力，培養學生的創新意識具有重要的現實意義.