一次數學教研活動引發的探究

☉貴州省綏陽縣小關中學 梁可霜

在一次數學教研活動上，筆者遇到了這樣的問題：“有一個三角形，其內角分別為：20°，40°，120°.怎樣把三角形分成兩個等腰三角形？畫出圖形，試試看，將此題從特殊推廣到一般，可變為△ABC滿足什么條件，可以用過頂點的一條直線將它分割成兩個等腰三角形？如何分？有幾種分法？筆者對此問題進行了探究，現寫出來以供同行參考.

筆者認為，過最小角的頂點的直線不能把原來的三角形分割成兩個等腰三角形.這個“問題”與角有關，所以我們不妨從角的角度去思考，應當首先找到度數最小的角（后面簡稱“最小角”，其次，度數最大的角簡稱“最大角”，介于兩者之間的角簡稱“次大角”）.

已知：如圖1，△ABC中，∠ABC＜∠A，∠ABC＜∠C，∠ABC是△ABC中的最小角，過點B的直線BD把△ABC分割成△ABD和△CBD，則兩個三角形不可能同時是等腰三角形.

圖1

證明： 在△ABD中，∠A＞∠1，∠3＞∠C＞∠ABC＞∠1，在△CBD中，∠C＞∠2，∠4＞∠A＞∠ABC＞∠2，可見，只剩下∠3=∠A，∠4=∠C的可能性了，那么它們能不能同時成立呢？因為∠3+∠4=180°，所以∠A+∠C=180°，顯然這個結論是不可能的，所以，∠3=∠A與∠4=∠C不能同時成立.

于是得出以下結論：

結論1：過最小角的頂點的直線不能把原來的三角形分割成兩個等腰三角形.

結論2：三角形有三個相等的最小角，分割該等邊三角形為兩個較小的等腰三角形的直線不存在.

結論3：只有三個角都不相等和僅有兩個角相等的兩類三角形才有可能被分割成兩個等腰三角形.

下面，我們先從三角形三邊都不相等的三角形開始研究，還需要附加什么條件，使一個三角形具有過某個頂點的一條直線將它分割成兩個等腰三角形.

如圖2，在△ABC中，∠B＜∠ACB＜∠BAC，∠B為最小角，不能再分割，那么∠B將成為分割△ABC后得到的其中一個等腰三角形的角，運用分類討論思想，∠B可能是這個等腰三角形的頂角，也可以是底角，并且當∠B是底角時，又可以分為兩類：以AB為底邊或以BC為底邊.可見，就∠B而言，先分三大類：

1.當∠B為頂角時，以B為圓心，BA長為半徑作弧，交BC于D，作直線AD把△ABC分割成△ABD和△ACD，顯然△ABD是等腰三角形，欲使△ACD成等腰三角形，又可以分為三種情況考慮：∠C=∠DAC，或者∠C=∠ADC，或者∠DAC=∠ADC.但是，結合圖形仔細分析一下，因為∠ADB是銳角，所以∠ADC是鈍角，顯然只有∠C=∠DAC成立.

圖2

可以看出，當最大角是次大角的3倍時，從最大角中分割出一個與次大角相等的角，并且要求這個角與次大角有一條公用邊，那么分割最大角的這條直線把原來的三角形分割成兩個等腰三角形.

2.當∠B為底角且以AB邊為底邊時，作AB的垂直平分線DE交BC于點D，作直線AD，顯然△ABD是等腰三角形，欲使△ACD成為等腰三角形，也可分為三種情況考慮.

圖3

（2）當∠B為底角且以AB邊為底邊時，若∠C=∠ADC，設∠B=α（如圖4），則∠C=∠ADC=2α，所以∠C=2∠B.可以看出，當次大角是最小角的2倍時，從最大角中分割出一個與最小角相等的角，并且要求這個角與最小角有一條公共邊，那么分割最大角的這條直線把原來的三角形分割成兩個等腰三角形．

圖4

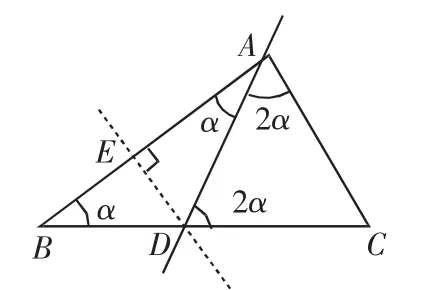
圖5

（3）當∠B為底角且以AB邊為底邊時，若∠DAC=∠ADC，設∠B＝α（如圖5），則∠DAC=∠ADC＝2α，所以∠BAC=α+2α=3α=3∠B.可以看出，當最大角是最小角的3倍時，從最大角中分割出一個與最小角相等的角，并且要求這個角與最小角有一條公用邊，那么分割成最大角的這條直線把原來的三角形分割成兩個等腰三角形．

3．當∠B為底角且以BC邊為底邊時，作BC的垂直平分線DE交AB于點D，過C、D兩點的直線CD把△ABC分割成△BCD和△ACD（如圖6），顯然△BCD是等腰三角形，欲使△ACD成等腰三角形，又可以分為三種情況考慮：∠A=∠ACD，或者∠A=∠ADC，或者∠ACD=∠ADC.但是結合圖形分析一下，因為∠A為最大角，∠ACB為次大角，所以淘汰掉∠A=∠ADC．

（1）當∠B為底角且以AB邊為底邊時，若∠A=∠ACD，設∠B＝α，（如圖6），則∠A=∠ADC＝2α，所以∠A=2∠B，可以看出：當最大角是最小角的2倍時，從次大角中分割出一個與最小角相等的角，并且要求這個角與最小角有一條公用邊，那么分割次大角的這條直線把原來的三角形分割成兩個等腰三角形．

圖6

圖7

（2）當∠B為底角且以BC邊為底邊時，若∠ACD=∠ADC，設∠B＝α（如圖7），則∠ACD=∠ADC=α+2α=3α，顯然∠ACB=3∠B.可以看出，當次大角是最小角的3倍時，從次大角中分割出一個與最小角相等的角，并且要求這個角與最小角有一條公用邊，那么分割次大角的這條直線把原來的三角形分割成兩個等腰三角形．

綜上所述，三個角都不相等的三角形分割成兩個等腰三角形的情形如下：

情形1：有一個角是90°.分割的方法：作斜邊上的中線所在的直線．

情形2：有一個角是另一個角的3倍（筆者為了能描述清楚，令這里的較小角叫“單倍角”，較大的角為“三倍角”）.有三種可能：最大角是最小角的3倍，或次大角是最小角的3倍，或最大角是次大角的3倍.分割方法：從三倍角中分割出一個與單倍角相等的角，并且要求這個角與單倍角有一條公用邊，即與這個角以單倍角為兩個內角構成一個較小的等腰三角形．

情形3：有一個角是最小角的2倍（筆者令這里的較大角叫“二倍角”，最大的角為“三倍角”，并且強調一下：必須是最小角的2倍）.有兩種可能：最大角是最小角的2倍，或次大角是最小角的2倍．分割方法：從第三個角（除最小角和“二倍角”）中分割出一個與最小角相等的角，并且要求這個角與最小角有一條公用邊，即以這個角與最小角為兩個內角構成一個較小的等腰三角形．

值得注意的是：當三角形的三個內角滿足上述的多種情形，比如既有3倍關系，又有2倍關系，那么分割方法可能不唯一．

接下來，我們研究：兩個角相等的等腰三角形，還需要附加什么條件，使該等腰三角形能分割成兩個較小的等腰三角形．

（1）當該等腰三角形只有一個最小角時，最小角必是頂角，另外兩個較大角是底角，如果我們把兩個相等的較大的底角，一個看成是最大角，另一個看成次大角，那么該等腰三角形上也有上面情形2、3的分割方法，只是要多考慮到等腰三角形的軸對稱性，分割該等腰三角形為兩個較小的等腰三角形的直線有兩條，研究過程與上面相似，這里就不一一敘述了．

（2）當該等腰三角形有兩個相等的最小角時，第三個角必是最大角且是頂角，兩個相等的最小角是底角，如果我們把兩個相等的最小的底角，一個看成是最小角，另一個看成次大角，那么該等腰三角形也有上述情形1、2的分割方法，當為情形2時，也要考慮等腰三角形的軸對稱性，研究過程與上面相似，這里省略．

問題1：在△ABC中，若過其中一個頂點的一條直線，將△ABC分成兩個等腰三角形，求△ABC各內角的度數．

解析：①如圖8，在△ABC中，若底角是頂角的2倍，設∠A＝α，∠B=∠C＝2α，則α＋2α＋2α＝180°，α＝36°，三內角的度數分別為：36°、72°、72°．

②如圖9，在△ABC中，若頂角是底角的2倍，設∠B=∠C＝α，∠A＝2α，則α＋α＋2α＝180°，α＝45°，三內角的度數分別為：90°、45°、45°．

③如圖10，在△ABC中，若頂角是底角的3倍，設∠B=∠C=α，∠A=3α，則α+α+3α=180°，α=36°，三內角的度數分別為：108°、36°、36°.

圖8

圖9

圖10

問題2：如果一個三角形有一個內角為40°，且過某一頂點能將該三角形分成兩個等腰三角形，則該三角形其余兩個角的度數是多少？

解析：①首先考慮，當這個三角形是直角三角形時，其余兩個角的度數是50°和90°.

②當這個40°的內角為最小角時，另外兩個較大的角可能與最小角有2倍或3倍關系，或者最大角是次大角的3倍，所以所得其余兩個角的度數為60°和80°.