基于遺傳自適應蟻群系統算法的中繼路由方法

陳可，胡曉光

(北京航空航天大學 自動化科學與電氣工程學院，北京，100191)

近年來，采用低壓電力線作為通信介質的傳輸技術具有充分利用現有資源、易施工、綜合成本低、不受環境條件限制等優點，是電力部門實現遠程自動抄表的發展趨勢，具有廣闊的應用前景。由于低壓電力線具有高噪聲、高衰減和高時變等特性[1-3]，使得集中器節點和目標電表節點之間直接通信成功概率較低，這不僅制約了信號傳輸的距離，同時嚴重降低了電力線通信的可靠性，進而影響抄表范圍和抄表成功率。因此在實際應用中，需要通過中繼技術來彌補以上缺憾。許多學者在這一領域進行了深入研究，提出了多種中繼路由方法，文獻[4]提出了具有中繼約束條件的自動中繼路由算法；趙杰衛等[5]采用蟻群算法及利用電氣距離作為約束條件候選集策略提高了中繼搜索的準確度和效率；劉曉勝等提出了一種適用于未知建筑物電力線拓撲結構條件下的蟻群電力線組網方法[6]，并通過仿真驗證了該組網算法的有效性和抗毀性；還提出了適用于低壓配電網電力線載波通信的類蟻群算法[7]，該方法可以有效延長電力線載波通信距離。以上這些方法在一定程度上解決了抄表范圍與抄表成功率等問題，但均有一些缺點：文獻[4]中的方法與一般自動中繼方法相比，雖然節約了抄表時間，提高了抄表成功率，但不具有動態適應電力線環境的變化能力；文獻[5-7]中的方法雖然能動態適應電力線環境的變化，但算法的收斂速度較慢，并且容易陷入局部極小值。針對以上問題，本文作者從提高抄表系統的時效性角度出發，將遺傳算法(Genetic algorithm，GA)和蟻群系統(Ant colony system，ACS)算法有機融合，提出了一種遺傳自適應蟻群系統(Genetic adaptive ant colony system，GAACS)算法。該算法利用 GA 的隨機搜索、快速性及全局收斂性等特點，獲得集中器到目標電表的初始中繼路由路徑并將其運用到蟻群算法初期信息素分布中，再利用蟻群系統算法的并行性、正反饋機制以及求解效率高等特性求出最終解。在求解過程中，為了防止算法陷入局部最優解，依據搜索情況對ACS算法中的狀態轉移概率因子、信息素揮發因子以及信息素強度等參數采取自適應調節策略。通過將本文算法、遺傳蟻群系統(Genetic ant colony system，GACS)算法、ACS和最大最小螞蟻系統(Max-min ant system，MMAS)算法進行對比仿真實驗，結果表明本文算法在收斂性、魯棒性、抗毀性及算法運行時間等方面均優于其他3種算法。

1 電力線載波抄表網絡拓撲結構

在低壓電力線載波抄表系統中，下行線路主要由集中器和一定數量的電表組成，在邏輯拓撲結構中可以將集中器視作網關，每個用戶電表視為可通信的終端節點。由于低壓電力線的干擾、信號衰減和負載的接入與切出等因素，使信號在電力線上的傳輸并不能和理想狀態時的傳輸距離相比，某些電表節點將不能直接與集中器節點進行通信。為了實現集中器對每一個目標電表的抄收，必須先建立集中器到部分電表之間的路由路徑，再將這些節點作為中繼節點進行數據的轉發，擴展通信距離，才可能將所有的節點連入低壓電力線抄表系統中，達到自動抄表的目的。抄表系統中，集中器與電表之間的樹形拓撲模型如圖1所示，集中器位于樹形拓撲結構的根部，即圖1中的0號節點，1～60號節點分別代表抄表系統中各電能表。

圖1 電力線載波抄表網絡樹形拓撲Fig.1 Power line carrier meter reading network tree topology

2 算法原理

2.1 遺傳算法原理

遺傳算法是一類可用于復雜系統優化的魯棒性搜索算法，它是模擬生物在自然環境中的遺傳和進化過程而形成的一種自適應全局概率搜索算法。遺傳算法是由可行解組成的群體逐代進化過程，選擇、交叉、變異是遺傳算法的3個主要過程[8-10]。

2.1.1 適應度函數及優化目標函數

適應度函數應該能夠反映出動態路由問題中解的優劣，通過群體的初始化，用式(1)計算每個個體的適應度F(X)，集中器到目標電表節點的路由路徑中，跳數相對越少，其適應度值越高，適應度函數定義為：

式中：F(X)為個體適應度值；Cmax為一個適當地相對比較大的數，本文所研究的抄表系統中，目標電表節點共60個，因此，Cmax取值為100；f(X)為個體相應的目標函數值，即動態路由路徑中源節點到目標節點的跳數。

2.1.2 選擇運算

為了加快遺傳算法的收斂速度，保留抄表過程中所獲得的較好路徑，本文采用精英選擇方法，該方法使適應度函數值高的個體不受交叉和突然變異的影響，而是無條件的遺傳給后代，由于作為最優個體的遺傳因子在群體中可能急劇地增多，算法能較快收斂到最優解或局部最優解。

2.1.3 交叉運算

該運算是交換2個染色體中的子路徑，其中用于交換的染色體必須擁有相同的源節點和目的節點。路徑交叉運算的交叉位置限制在2個染色體中都含有的節點(不包含源節點和目標節點)，從潛在的交叉位置中隨機選擇節點作為交叉位置，交換子路徑。圖2所示為將交叉運算應用于從集中器節點0到目標電表節點15的一對父代A1和A2的情況，父代潛在的交叉位置是中繼節點6，9和12，選擇中繼節點6作為交叉位置，圖2通過交換子路徑產生新的子代B1和B2。

圖2 交叉運算框圖Fig.2 Crossover operation figure

當一對染色體中的公共點不存在時交叉位置就不能選擇，因此也就不可能實施交叉運算。交叉概率pc取值過大會破壞群體中的優良模式，對進化運算產生不利影響；若取值過小，產生新個體的速度較慢。本文為了加快遺傳算法的收斂速度，交叉概率pc取值為0.5。

2.1.4 變異運算

該運算是從一個染色體產生另一個染色體。為了實現變異，從染色體中隨機選擇節點，該節點稱為變異節點，在滿足最小通信距離的條件下從與變異點相鄰節點中隨機選擇另一個節點，最后利用基于最小跳計數準則的Dijkstra算法分別產生從源節點到選擇點和從選擇點到目標節點的可選路徑。路徑變異運算如圖3所示，假設中繼節點6被選擇作為變異點，從變異節點的鄰點中選擇節點7，根據Dijkstra最小跳數算法產生源節點0到節點7的子路徑a及節點7到目標節點15的子路徑b，連接a和b，完成變異操作。為了避免路徑中的任何環，如果子路徑a和b中存在重復節點，子代B就不能產生。變異概率pm取值較大時，雖然能夠產生較多的新個體，但可能破壞很多較好的路徑，使得算法性能近似于隨機搜索算法的性能；若取值過小，則變異操作產生新個體的能力和擬制早熟現象的能力就會較差。本文為了加快遺傳算法的收斂速度，變異概率pm取值為0.01。

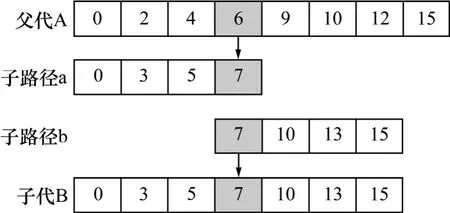
圖3 變異運算框圖Fig.3 Mutation operation figure

2.2 基本蟻群系統算法原理

蟻群系統算法是近年發展起來、受自然界螞蟻搜尋食物行為啟發得到的并行優化算法[11-15]。該算法具有采用分布式并行計算機制、易于與其他方法結合、具有較強的魯棒性等優點，但搜索時間長、易陷入局部最優解是其最為突出的缺點。

2.2.1 路徑構建

在ACS算法中，位于城市i的螞蟻k，根據偽隨機比例規則選擇城市j作為下一個訪問的城市，路徑轉移規則如下：

式中：q0(0＜q0＜1)是狀態轉移因子；q為0到1之間的隨機數；ηil為啟發式信息；β為期望啟發式因子；若y=f(x)，則argmax[y]表示當y取得最大值時x的值。當q≤q0時，按照先驗規律選擇路徑；當q＞q0時，按照概率進行路徑搜索。

轉移概率計算公式如下：

式中：τij為路徑(i，j)上的信息素大小；ηij為路徑(i，j)上的啟發式信息大小；α為信息啟發式因子；β為期望啟發式因子。

2.2.2 局部信息素更新

在路徑構建過程中，螞蟻每經過一條邊(i，j)，都將立刻調用局部信息素規則更新該邊上的信息素，規則如下：

式中：τij為路徑(i，j)上的信息素含量；ξ為局部更新揮發因子；τ0為信息素初始值。ξ的引入使被選擇過的路徑上的信息素減少。局部更新規則使螞蟻傾向于選擇沒有走過的路徑，避免搜索過于集中到同一條線路上，使得算法不會陷入停滯狀態，這種更新規則有利于新路徑的發現。

2.2.3 全局信息素更新

在ACS算法中，只有一只螞蟻(至今最優螞蟻)被允許在每一次迭代之后釋放信息素，全局信息素更新規則如下：

式中：τij為路徑(i，j)上的信息素含量；Δτij為路徑(i，j)上的信息素增量；ρ為信息素揮發因子；Q為信息素強度；Lbs為至今最優路徑長度。對至今最優線路進行信息素增加，可使搜索過程具有指導性，搜索范圍集中在至今最優線路。

2.3 自適應蟻群系統算法原理

基本蟻群系統算法在搜索初期，各條路徑上的信息素分布比較分散，在經過一定的迭代步數后，信息素會逐漸集中到少數路徑上，搜索的大致方向也就隨之確定，由于ACS算法的正反饋機制旨在強化性能較好的解，因此，在搜索后期，當某些路徑上的信息素強度明顯高于其余路徑時，繼續搜索將會總在少數路徑上進行，這樣會使解的結構過于相似，搜索過程也會停頓下來，算法容易陷入局部最優解。

本文采用遺傳算法得到集中器到某目標電表的初始路徑，并將其運用到蟻群系統算法初期信息素分布中，這將導致在算法初期，少數路徑上的信息素強度會明顯高于其余路徑，算法極易出現停滯現象并陷入局部最優解而無法跳出。為了解決這個問題，本文在ACS算法的基礎上，提出了根據解的搜索情況，動態自適應調整狀態轉移概率因子、信息素揮發因子、信息量強度等因素，可在一定程度上有效地克服 ACS算法的一些不足。

2.3.1 轉移概率因子的改進

在式(2)中，狀態轉移因子q0是一個非常重要的參數。當q≤q0時，螞蟻依據信息素的積累量和啟發式信息值確定要移動的下一節點；當q＞q0時，螞蟻依據概率有偏向性地探索各條邊。在基本蟻群算法中，q0是區間[0，1]上的固定常數，缺乏自適應性。本文通過自適應調整參數q0來調節算法對新路徑的探索度，從而決定算法是應該集中搜索至今最優路徑附近的區域，還是應該搜索其他區域，q0按下式進行選擇：

由于抄表系統中，終端電表的數量較多，因此，在算法執行初期，選擇相對較大的q0能加快算法的收斂速度，降低算法的隨機性，利于局部搜索；在算法執行中期，選擇相對較小的q0能提高算法隨機性，利于全局搜索；在算法執行后期，重新恢復q0的初始值，進一步提升收斂速度并最終找到全局最優解。

2.3.2 信息素揮發因子的改進

蟻群系統算法中信息素揮發因子ρ的大小直接關系到ACS算法的全局搜索能力及其收斂速度。在自動抄表系統中，如果終端電表數量比較多，由于ρ的存在，會使那些從來未被搜索到的路徑上的信息量減小到接近于 0，因而降低了算法的全局搜索能力，而且當ρ過大時，以前搜索過的路徑被再次選擇的可能性過大，也會影響到算法的隨機性能和全局搜索能力；反之，通過減小ρ雖然可以提高算法的隨機性能和全局搜索能力，但又會使算法的收斂速度降低。基于以上分析，本文采取自適應調整信息素揮發因子ρ的方法，在提高收斂速度的同時避免陷入局部最優解，當算法在連續N次循環迭代過程中，最優解都沒有變化，表明搜索過程可能陷入了局部最優解，此時ρ按照下式作自適應調整：

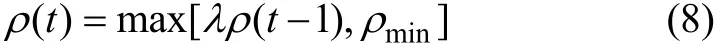
式中：ρmin為ρ的最小值，為了防止ρ過小降低算法的收斂速度；λ為預先設定的衰減系數，根據抄表規模調整。式(8)使得信息素揮發因子ρ從最大值逐漸降低，但又不至于太低而影響算法的收斂速度。與式(5)對比可以看出：改進前的ρ是一個固定值，而改進之后，在算法運行初期，ρ取相對較大值，提高算法的收斂速度，快速找到局部最優解；在算法運行后期，ρ取相對較小值，可以進一步提高隨機性能和全局搜索能力。

2.3.3 信息素強度的改進

信息素強度Q為螞蟻循環一周時釋放在所經過路徑上的信息素總量，其作用是為了充分利用路徑上的全局信息反饋量，使得算法在正反饋機制作用下以合理的演化速度搜索到所求問題的全局最優解。Q越大，則在螞蟻已遍歷路徑上信息素的累積加快，可以加強蟻群搜索時的正反饋性能，有助于算法的快速收斂，但此時算法的全局搜索能力變差，極易陷入局部最優解，計算性能也變得很不穩定；Q過小又會影響算法的收斂速度。針對以上問題，本文提出了一種根據蟻群算法搜索情況來自適應動態修改信息素強度的方法，可在一定程度上有效地解決擴大搜索空間和尋找最優解之間的矛盾，從而使得算法跳離局部最優解。當算法在連續N次循環迭代過程中，最優解都沒有變化，表明搜索過程可能陷入了局部最優解，則采用強制機制，減小要添加的信息素，使算法從局部極小值中逃脫出來。此時Q按照下式作自適應調整：

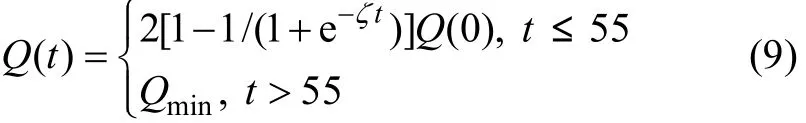
式中：ζ為正參數，控制Q(t)的下降速度；Q(0)為信息素強度的初始值；Qmin為Q(t)的最小值。采用時變遞減函數代替常數項Q，可以保證在路徑上的信息素隨搜索過程逐漸增多的情況下，繼續保持隨機搜索和路徑信息的啟發作用間的平衡，使算法能跳出局部最優，繼續尋找全局最優解。

3 基于 GAACS路由算法的特點及步驟

3.1 路由算法特點

電力線載波抄表系統中，集中器與各用戶電表的連接關系通常未知，通信網絡邏輯拓撲結構處于盲態，路由算法須具有如下特點：

(1) 算法能適應盲網絡狀態要求。在盲網絡狀態下，指定中繼方式已經不能滿足路由要求，路由算法須具有對抄表系統網絡探索和辨識的能力，找到集中器節點和目標電表節點之間路由線路，同時算法應具有路由優化能力，搜索并收斂于優良的路由線路。

(2) 路由算法能夠適應抄表系統中網絡邏輯拓撲的變化。抄表系統中不斷有新的用戶接入網絡，導致系統的邏輯拓撲不斷變化，路由算法要能夠適應該變化，對變化前后的邏輯拓撲結構，算法的路由能力不變。

(3) 路由算法有較強的抗毀性。低壓電力線具有負載多、噪聲強、衰減大、時延長等特征，抄表通信路徑易失效，網絡中電表節點本身也存在硬件故障等異常情況。要求路由算法能夠在抄表通信線路被破壞時迅速重構，提高抄表系統的抗毀性。

3.2 基于GAACS路由算法實現步驟

在闡述利用GAACS算法實現抄表系統動態路由過程之前，對本文常用的名詞進行定義。

定義1 搜索螞蟻壽命：是指搜索螞蟻數據幀能夠被中繼電表節點轉發次數的上限。在實際抄表系統中，數據幀不能被無限次轉發，尤其是對于窄帶電力線載波通信，通信速率較低，數據幀轉發次數受到較大限制，否則占用信道時間過長，同時也容易產生錯誤。考慮該約束條件，算法中定義螞蟻壽命變量為 7，表示每只搜索螞蟻最多能夠經歷7個不同的中繼節點，每轉發一次該值減1。如果在經歷了7個電表節點之后，該搜索螞蟻沒有找到目標電表節點，則設定該螞蟻死亡，不再繼續尋找，工程應用中表現為舍棄該數據幀不再轉發。

定義2 跳數：是指集中器節點與任意一個目標電表節點通信時，搜索螞蟻數據幀到達目標電表節點所需被轉發的次數。可以直接通信的節點，跳數為 0；需要通過1個中間電表節點轉發數據幀，跳數為1，以此類推。

定義3 通信距離：是指抄表系統中可以相互通信的兩個節點所跨過的節點個數加 1。該距離會隨著電力線信道質量而變化。本文規定任意一個節點最小可通信距離可以跨過2個節點，即通信距離為3，實際抄表系統中，各個電表節點的通信距離會遠大于3。

GAACS算法設計了合理有效地適應度函數和優化目標函數，并且采用通信距離、螞蟻壽命作為約束條件，力求在保證抄表正確和可靠的前提下盡量提高路由效率。在該算法中，約定如下：①在集中器節點控制范圍內每個電表節點有一個唯一的地址編號；②抄表系統邏輯拓撲圖為無向圖；③任意相鄰的兩個電表節點都能夠保證可靠通信。GAACS算法流程如下，其中，步驟1～8利用遺傳算法的快速全局搜索能力生成路徑初始信息素分布，步驟 9～15利用蟻群算法的正反饋收斂機制完成最終集中器到目標電表之間最優路徑的建立。

步驟1 參數初始化。主要包括以下幾方面：① 群體規模M、交叉概率pc、變異概率pm、信息啟發式因子α、期望啟發式因子β、信息素常量τC、等效信息素τG、信息素強度初始值Q(0)、信息素強度最小值Qmin、信息素揮發因子最小值ρmin、轉移概率因子最小值qmin、局部更新揮發因子ξ、系數σ，λ和ζ；② 集中器及各電表節點通信信息表、轉移概率表、啟發信息表、禁忌表初始化；③ 遺傳迭代次數NG、蟻群迭代次數NA、迭代螞蟻數m初始化；

步驟2 編碼。利用序列編碼方法，編碼位串的首個字符代表集中器編號，設定為 0，編碼位串最后一個字符代表目標電表節點編號，中間字符按照抄表路由路徑順序依次排列。如果路徑不符合最小通信距離的約束條件，則不能被編譯成一個染色體，這意味著路徑中的每一步都必須經過抄表系統中實質上的連接；

步驟3 初始化群體。針對某一目標電表節點，利用基于最小跳計數準則的 Dijkstra算法產生從集中器節點到目標節點的路徑作為初始路徑。為了提高遺傳算法的運行效率，避免搜索中繼路由路徑的時間過長，初始群體規模不宜太大；

步驟4 根據式(1)計算種群內個體適應度值、判斷迭代次數nG，若nG＞NG，獲得優化抄表路由路徑并轉向步驟9，否則轉向步驟5；

步驟5 記錄父代的精英個體，將父代中的精英個體直接復制到子代種群中；

步驟6 以概率pc對種群進行路徑雜交運算；

步驟7 以概率pm對種群進行路徑變異運算；

步驟8 由精英復制個體、交叉、變異后的個體構成下一代種群個體，轉入步驟4；

步驟9 經過遺傳算法得到集中器到目標電表的優化抄表路徑，并運用到蟻群算法初期信息素分布中，用下式更新各條路徑上的初始信息素分布：

式中：τC是給定的一個信息素常數；τG則是根據遺傳算法求得的初始抄表路徑所對應的等效信息素。

步驟10 集中器節點發起探索螞蟻數據幀。該數據幀包括集中器地址、目標電表地址、路由區及搜索螞蟻壽命。路由區在數據幀到達目標電表節點之前不斷填充其所經歷路由節點地址信息。依據算法運行時間，按式(7)自適應調整狀態轉移概率因子q0(t)，螞蟻按式(2)選擇下一個訪問的節點，并立即按式(4)更新局部信息素濃度；

步驟11 判斷是否為目標節點，如果是目標節點轉入步驟12，否則轉入步驟10；

步驟12 對每一只螞蟻執行步驟10和11，直到所有的螞蟻均迭代完成；

步驟13 找出至今最優螞蟻，并按式(5)和(6)進行至今最優路徑的全局信息素濃度更新；

步驟14 當算法在連續N次循環迭代過程中，最優解都沒有變化，表明搜索過程可能陷入了局部最優解，根據式(8)和(9)自適應調整信息素揮發因子ρ(t)及信息素強度Q(t)；

步驟15 判定算法是否達到設定的迭代次數NA，達到則記錄集中器節點到目標電表節點的最優路徑，并把最優路徑存到集中器節點的路由表中，否則轉向步驟10。

4 仿真結果

本文仿真實驗中各參數選擇為：種群規模M=20，交叉概率Pc=0.5，變異概率等效信息素τG=2，每次迭代螞蟻數m=15，螞蟻壽命N=4，NA=42。說明，在4.2和4.3中遺傳算法迭代次數NG取值為4；蟻群算法迭代次數NA取值為26；參數自適應調整時最大迭代次數N取值為3。

4.1 算法收斂性分析

算法的收斂性是衡量算法性能優劣的重要指標之一，本文采用MATLAB7.01為仿真平臺，對GAACS，GACS，ACS和MMAS 4種算法下，集中器節點0到目標電表節點60的抄表路由路徑尋優進行驗證，仿真采用的物理拓撲結構如圖 1所示，仿真結果如圖 4所示。

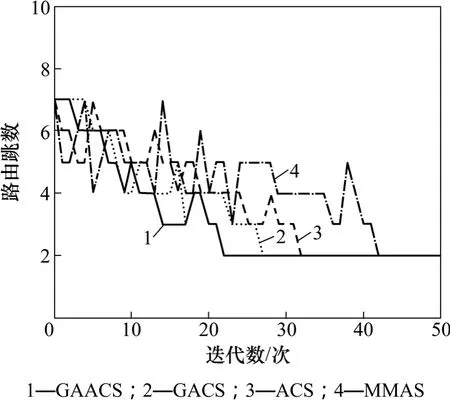
圖4 搜索電表節點60的仿真結果Fig.4 Result of simulation about searching meter node 60

從圖4可以看出：4種算法經過不同次數的迭代運算后均能收斂到最優路由路徑：0→19→51→60或者 0→19→50→60，從搜尋到最佳路由路徑的效率方面比較，顯然GAACS算法搜尋到最優解的效率最高，僅僅經過 22次迭代運算就收斂到最優解；其次是GACS算法，經過27次迭代運算收斂到最優解；再是ACS算法，經過32次迭代運算收斂到最優解；搜索效率最低的是MMAS算法，經過42次迭代運算才最終找到最優解。因此，相比其他 3種算法，GAACS算法能更好地適用于電力線載波抄表系統中繼路由問題，該算法具有較高的動態路由尋優效率，能夠確保抄表路由路徑的質量。

4.2 算法魯棒性分析

算法魯棒性是指算法適應不同網絡拓撲結構的能力，在實際抄表系統中，集中器與各電表之間的物理拓撲結構非常復雜，由于低壓電力線信道質量的變化引起電表節點通信距離的變化，導致抄表系統的物理拓撲結構隨之變化；此外，隨著電表節點的加入與退出也會導致物理拓撲結構的變化。GAACS算法能否適應這種復雜性，是該算法能否運用到實際電力線載波抄表系統的重要評判標準。

為了更好地反映電力線載波抄表系統中通信網絡邏輯拓撲的時變性，設某時刻各電表節點通信距離是在一定范圍內的隨機值，仿真分析這種情況下GAACS算法搜索最佳路由路徑的能力。仿真中仍然采用圖 1所示的拓撲結構，但每個電表節點的通信距離為 1～5之間的一個隨機值。表1所示為仿真實驗中各電表節點隨機產生的通信距離表，其中N表示電表節點號，D表示該電表節點通信距離。

圖5所示為采用表1中的電表節點隨機通信距離(集中器節點的通信距離設定為 2)，運用 GAACS，GACS，ACS和MMAS等算法求取集中器節點0到目標電表節點60的抄表路由路徑尋優仿真結果。

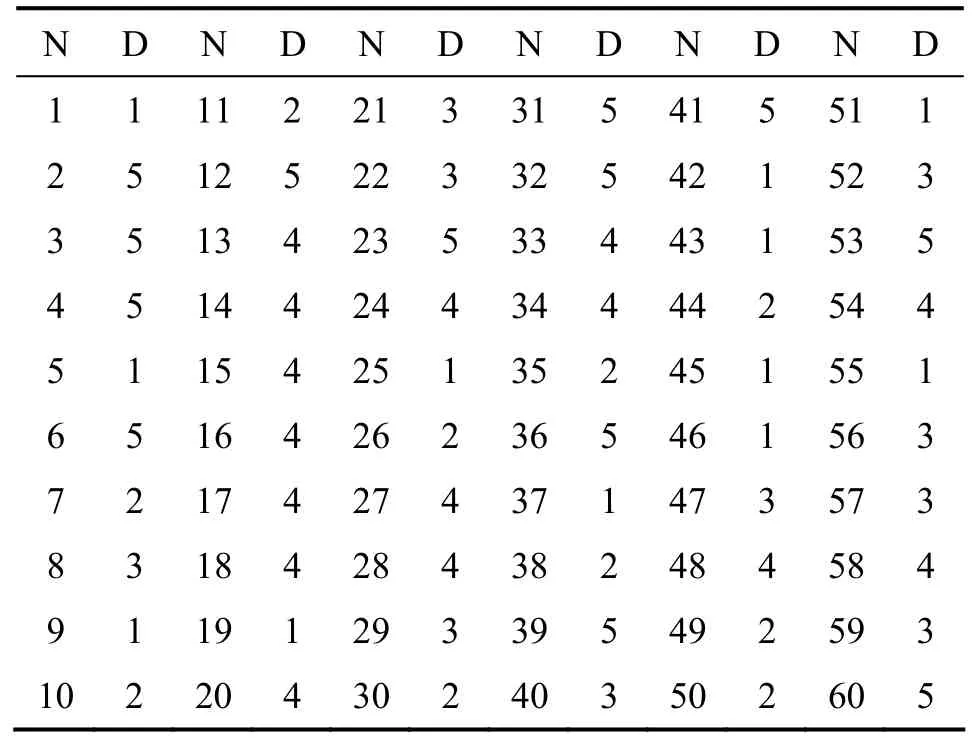
表1 各電表節點通信距離隨機值Table 1 Random value of meter node communication distance

圖5 隨機通信距離仿真結果Fig.5 Result of simulation about random communication distance

從圖5可以看出：在實際低壓電力線載波抄表系統各電表節點通信距離隨機的情況下，只有 GAACS算法能夠最終搜索到最優路由路徑，即：0→8→41→60或0→2→41→60，算法收斂到最少路由跳數2跳時所需的迭代數僅為 13次。而 GACS，ACS和 MMAS 3種算法對于節點通信距離隨機的抄表系統，均未能收斂到最優路由路徑并全部陷入局部最優解。原因是GAACS算法能夠依據當前的搜索情況自適應地改變狀態轉移因子、信息素揮發因子、信息素強度等參數，使得在算法陷入局部最優解后，仍然能夠跳出局部最優解，繼續尋找全局最優解，在保證收斂速度的條件下提高了解的全局性。因此，可以得出以下結論：GAACS算法的魯棒性能最好，GACS，ACS和MMAS 3種算法的魯棒性能大致相當。

4.3 算法抗毀性分析

低壓電力線具有噪聲強、衰減大、負載多、時延長等特征，通信路徑易失效，抄表系統中，電表節點本身也存在硬件故障等異常情況。要求路徑尋優算法能夠在系統中部分通信線路被破壞時迅速重構，提高抄表系統的抗毀性。

仿真中仍然采用圖1所示的拓撲結構，假設某個時刻19號電表節點發生故障，喪失通信功能，則此電表節點在系統網絡邏輯拓撲中消失，此時含有19號電表節點的路由線路將不再適用，某些集中器到目標電表節點的抄表路徑需要重新組建。對該情況進行仿真實驗，假設節點的通信距離為3，以60號電表節點作為目標節點，分別采用GAACS，GACS，ACS和MMAS算法，仿真結果如圖6所示。

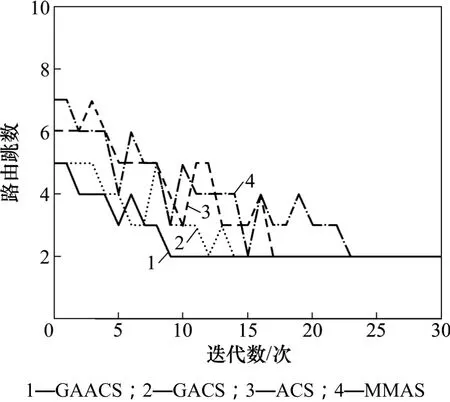
圖6 節點失效仿真結果Fig.6 Result of simulation about node failure

從圖6可以看出：在19號節點發生故障的情況下，GAACS，GACS，ACS和MMAS算法再次搜索到最優路由路徑所需的迭代數分別為9，14，17和23次，顯然GAACS算法具有更高的搜索效率。GAACS算法僅僅需要9次迭代搜索，路由跳數就最終收斂到2跳，多次仿真實驗輸出的路由線路均為以下7條線路中的1 條，即 0→8→41→60，0→8→50→60，0→8→51→60，0→30→41→60，0→30→50→60，0→30→51→60 和0→30→57→60。這些路徑均為最優路由路徑。因此，在實際低壓電力線載波抄表系統中，因某電表節點自身發生故障或線路故障引起整個抄表系統拓撲結構發生變化時，GAACS算法不僅能夠針對新的拓撲結構迅速找到最優路由路徑，提高抄表系統的抗毀性，而且與其他3種算法相比，GAACS算法能夠以相對較少的迭代次數收斂到最優路徑，從而縮減集中器到目標電表的中繼路由路徑尋優時間，提升整個抄表系統的時效性。

4.4 算法性能指標比較

為了綜合比較GAACS，GACS，ACS和MMAS 4種算法的性能，本文依然采用圖1所示的網絡拓撲結構，分別選取31～60號節點作為目標節點，采用上面 4種算法對每一個目標節點進行一次路徑尋優實驗，實驗結果如表2所示。

表2 實驗結果Table 2 Experimental results

從表2可以看出：對30個目標電表節點路由路徑尋優實驗中，在收斂到最優解節點數量方面，如果采用GAACS算法，集中器節點對其中25個目標電表節點能搜索到最優路由路徑，僅對5個目標電表的尋優陷入了局部最優解，而采用 GACS，ACS和 MMAS 3種算法，收斂到最優解的節點個數分別為23，20和19，收斂到次優解的節點個數分別為7，10和10；對于所有節點收斂時迭代次數平均值方面，GAACS算法所需的迭代數平均值最少，僅為12.16次，遠低于MMAS算法的36.28次；對于收斂到最優解所需平均運算時間方面，GAACS算法的平均運算時間也明顯優于其他3種算法。這是因為GAACS算法利用了遺傳算法的快速全局搜索能力，并在迭代過程中依據搜索情況對蟻群系統算法的相關參數作自適應調整，有效地克服了蟻群算法搜索時間長、易陷入局部最優解等缺點。

5 結論

(1) 針對實際電力線載波抄表系統中現有中繼路由算法的不足，提出了一種基于遺傳自適應蟻群系統算法的動態中繼路由方法，利用遺傳算法的快速全局搜索能力獲得路徑信息素的初始分布，再結合蟻群算法的正反饋收斂機制，同時依據搜索情況對狀態轉移概率因子、信息素揮發因子、信息素強度等參數進行自適應調整，最終獲得最優路由線路。

(2) 將GAACS與GACS，ACS和MMAS算法在算法收斂性、魯棒性、抗毀性以及運算時間方面進行了比較。結果表明GAACS算法不僅具有動態路由路徑尋優功能，而且有效地克服了基本蟻群系統算法收斂速度慢、易陷入局部極小值等問題，提高了整個抄表系統的時效性。隨著抄表系統中目標電表節點的規模增大，改進的效果越明顯。

[1]趙陽, 董穎華, 陸婋泉, 等.EMI噪聲分離網絡在電力線噪聲分析中的應用[J].中國電機工程學報, 2010, 30(21)∶ 114-120.ZHAO Yang, DONG Yinghua, LU Xiaoquan, et al.EMI noise discrimination network applied to power-line EMI noise analysis[J].Proceedings of the CSEE, 2010, 30(21)∶ 114-120.

[2]羅文亮, 柯熙政, 馬鳴.基于低壓電力線通信信道的自適應估計研究[J].儀器儀表學報, 2009, 30(8)∶ 1623-1629.LUO Wenliang, KE Xizheng, MA Ming.Study of adaptive estimation based on low-voltage power-line communication channel[J].Chinese Journal of Scientific Instrument, 2009, 30(8)∶1623-1629.

[3]徐志強, 翟明岳, 趙宇明.基于電力線信道作用的能量時頻分布及其能量分配[J].電力系統自動化, 2009, 33(1)∶ 75-80.XU Zhiqiang, ZHAI Mingyue, ZHAO Yuming.Energy time frequency distribution based on power line channel effect and its application in energy assignment[J].Automation of Electric Power Systems, 2009, 33(1)∶ 75-80.

[4]陳可, 胡曉光.基于電力線寬帶載波集中器設計與中繼算法[J].電力自動化設備, 2011, 31(9)∶ 115-120.CHEN Ke, HU Xiaoguang.Design of concentrator based on electric line broadband carrier and relay routing algorithm[J].Electric Power Automation Equipment, 2011, 31(9)∶ 115-120.

[5]趙杰衛, 盧文冰, 李賢亮.電力線載波自動抄表動態路由技術研究[J].電力系統通信, 2007, 28(11)∶ 1-5.ZHAO Jiewei, LU Wenbing, LI Xianliang.Research of dynamic routing technology in automatic meter reading system based on power line carrier[J].Telecommunications for Electric Power System, 2007, 28(11)∶ 1-5.

[6]劉曉勝, 戚佳金, 宋其濤, 等.基于蟻群算法的低壓配電網電力線通信組網方法[J].中國電機工程學報, 2008, 28(1)∶ 71-76.LIU Xiaosheng, QI Jiajin, SONG Qitao, et al.Method of constructing power line communication networks over low-voltage distribution networks based on ant colony optimization[J].Proceedings of the CSEE, 2008, 28(1)∶ 71-76.

[7]劉曉勝, 周巖, 戚佳金.電力線載波通信的自動路由方法研究[J].中國電機工程學報, 2006, 26(21)∶ 76-81.LIU Xiaosheng, ZHOU Yan, QI Jiajin.Method study of automatic routing for power line communication[J].Proceedings of the CSEE, 2006, 26(21)∶ 76-81.

[8]Murat A, Novruz A.Development a new mutation operator to solve the traveling salesman problem by aid of genetic algorithm[J].Expert Systems with Applications, 2011, 38(3)∶1313-1320.

[9]Semya E, Jacques T, Taicir L.Multiple crossover genetic algorithm for the multiobjective traveling salesman problem[J].Electronic Notes in Discrete Mathematics, 2010, 36(1)∶939-946.

[10]雷友誠, 涂祖耀, 桂衛華, 等.基于遺傳蟻群算法的樹枝型鐵路取送車問題優化[J].中南大學學報∶ 自然科學版, 2011,42(8)∶ 2356-2362.LEI Youcheng, TU Zuyao, GUI Weihua, et al.Optimization of placing-in and taking-out wagons on branch-shaped railway lines based on genetic and ant colony algorithm[J].Journal of Central South University∶ Science and Technology, 2011, 42(8)∶2356-2362.

[11]YANG Jingan, ZHUANG Yanbin.An improved ant colony optimization algorithm for solving a complex combinatorial optimization problem[J].Applied Soft Computing, 2010, 10(2)∶653-660.

[12]ZHAO Dongming, LUO Liang, ZHANG Kai.An improved ant colony optimization for the communication network routing problem[J].Mathematical and Computer Modelling, 2010,52(11)∶ 1976-1981.

[13]WANG Hua, XU Dong, YI Shanwen, et al.A tree-growth based ant colony algorithm for QoS multicast routing problem[J].Expert Systems with Applications, 2011, 38(9)∶ 11787-11795.

[14]焦亞萌, 黃建國, 侯云山.基于蟻群算法的最大似然方位估計快速算法[J].系統工程與電子技術, 2011, 33(8)∶ 1718-1721.JIAO Yameng, HUANG Jianguo, HOU Yunshan.Fast maximum likelihood direction-of-arrival estimation based on ant colony optimization[J].Systems Engineering and Electronics,2011, 33(8)∶ 1718-1721.

[15]張煜東, 吳樂南, 韋耿, 等.基于自適應蟻群算法的軟硬件劃分[J].控制與決策, 2009, 24(9)∶ 1385-1389.ZHANG Yudong, WU Lenan, WEI Geng, et al.Hardware/software partition using adaptive ant colony algorithm[J].Control and Decision, 2009, 24(9)∶ 1385-1389.