一種K－分布雜波參數估計方法

徐 偉，陳永森

（船舶重工集團公司723所，揚州225001）

0 引 言

在K－分布雜波背景中進行恒虛警處理或者信號檢測時，需要準確估計其分布參數，較大的估計誤差會導致較高的虛警概率。國內外學者對K－分布的參數估計進行了大量的研究，目前最有效的參數估計方法是最大似然法。由于K－分布的解析形式相對復雜，最大似然估計的解析式很難獲得，其參數估計需要用數值方法在二維參數平面內進行搜索［1］，計算量較大。此外，基于最大期望值（EM）的方法［2］以及基于神經網絡估計的方法［3］需要多次迭代，實現復雜，收斂時間較長，因此工程上大都采用運算相對簡單的矩量法［4－5］。這種方法受噪聲和數據長度的影響較大，個別樣本甚至無法得出計算結果。Blacknell將矩量法進行了推廣［6］，即利用xln（x）的各階期望進行參數估計，但仍然無法滿足實際雜波處理要求。本文針對該問題，從工程應用角度出發，提出利用ln（x）的一、二階矩求解K－分布雜波的形狀參數和尺度參數的方法，這種方法受噪聲影響較小，能夠有效避免錯誤估計的發生，仿真和實測雜波數據處理表明了該方法的準確性和有效性。

1 參數估計

K－分布的概率密度函數為［4］：

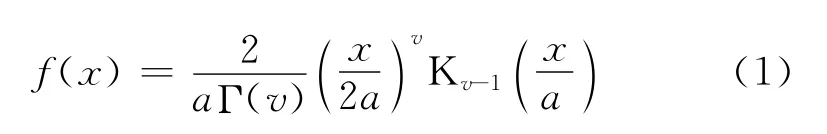
式中：Γ（·）為伽馬函數；Kv－1為v階第二類修正貝塞爾函數；a為尺度因子，a＞0；v為形狀參數，v＞0，v越大，f（x）越向右偏離，x＞0。

K－分布的r階矩［4］為：

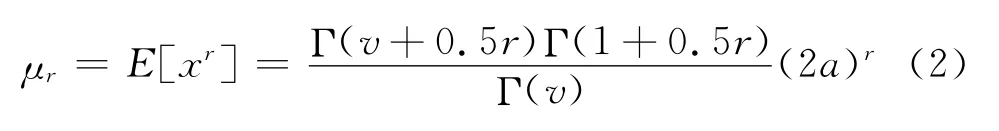
文獻［4］提出利用K－分布的各階矩估計其參數的方法，即：

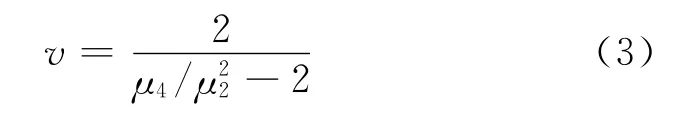
由式（2）得：

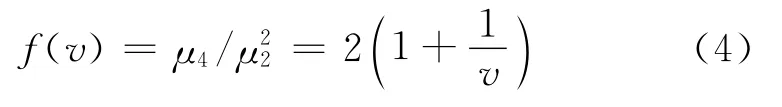
實際雜波處理中，當雜波的形狀參數v較大時，由式（4）知，f（v）≈2。當受到噪聲和有限數據長度的影響時，通過數值方法獲得的二、四階矩存在誤差，個別樣本出現的情況，此時利用式（3）進行估計，會得出的錯誤估計結果。文獻［6］提出的基于xln（x）的方法亦是如此。針對該問題，本文提出利用xln（x）的一、二階矩估計K－分布參數估計方法，避免錯誤估計的發生，提高估計精度。

令z＝ln（x），由式（1）得z的一階原點矩為：

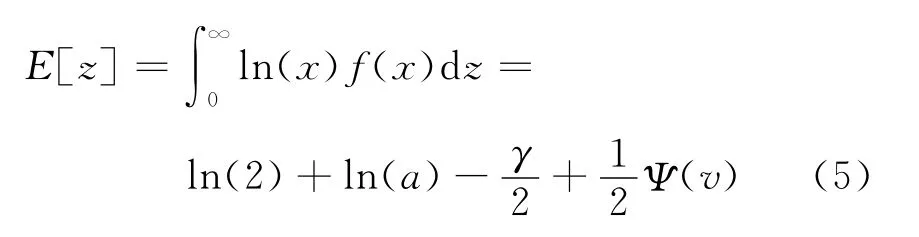
式中：γ為常數；Ψ（·）為Psi函數。

z的二階原點矩：

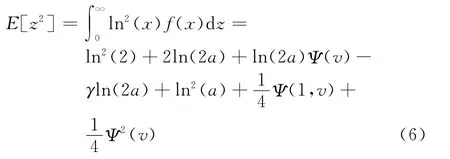
由于ln（2a）＝ln（2）＋ln（a），故可得：

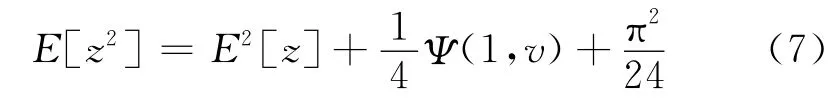
式中：Ψ（1，·）為一階Psi函數。

式（7）即為形狀參數的估計表達式，利用數值方法獲得z的一、二階原點矩求解式（7）即可得到估計值）的值可以通過查表獲得。由式（4），得尺度參數a的估計值：

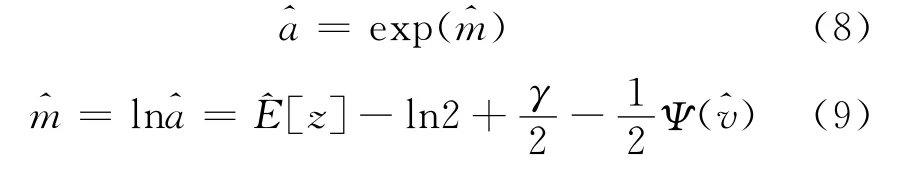
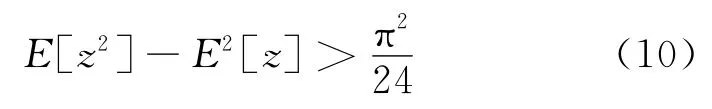
當通過數值方法獲得的z的一、二階矩存在誤差時，該方法在E［z］和E［z2］之間提供了余量，保證估計式（7）有解，減少了錯誤估計的出現。

2 有效性與精度分析

由于K－分布的形狀參數v＞0，設估計結果0的為有效估計，定義估計有效率ρ為有效估計次數與總估計次數之比。為驗證本文方法的估計有效率和估計精度，進行了仿真分析，利用計算機生成不同形狀參數的K－分布數據，數據樣本點數512個，采用本文方法、常規矩估計方法和xln（x）方法分別進行參數估計，對每個形狀進行1 000次仿真，3種方法的估計有效率ρ隨形狀參數的變化關系如圖1所示。

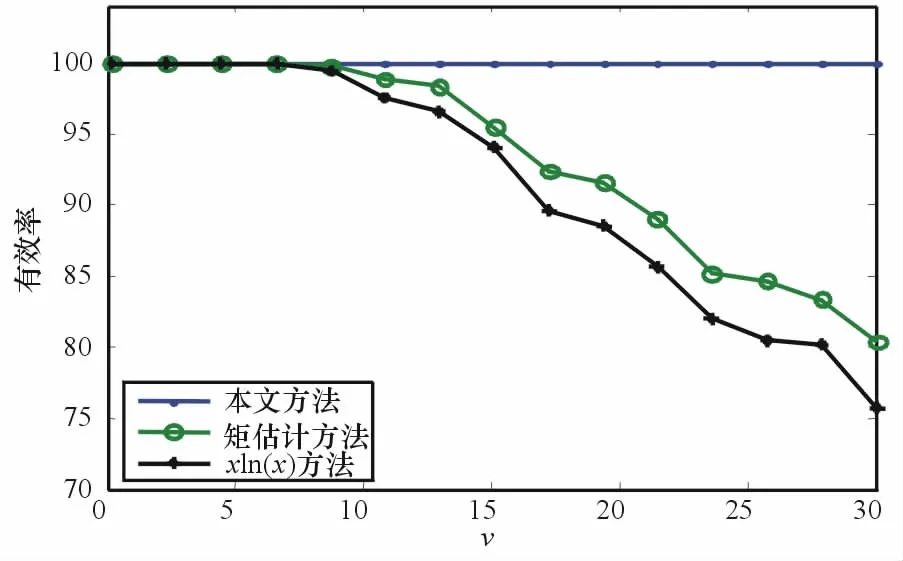
圖1 估計有效率

可以看出，當v較小時，3種方法均能以較高的ρ進行估計，但隨著v的增大，矩估計方法和xln（x）法的估計有效率逐漸減小，這與分析一致，而本文方法不受此影響。圖2給出了3種方法的估計精度，估計精度通過相對誤差表征，可以看出3種方法估計精度受形狀參數v的影響較大，當v＜15時，xln（x）法具有較高的估計精度，本文方法的相對估計誤差較大，但在30%以內，能夠滿足工程要求；當v＞15時，本文方法或矩估計方法給出最小的估計誤差。

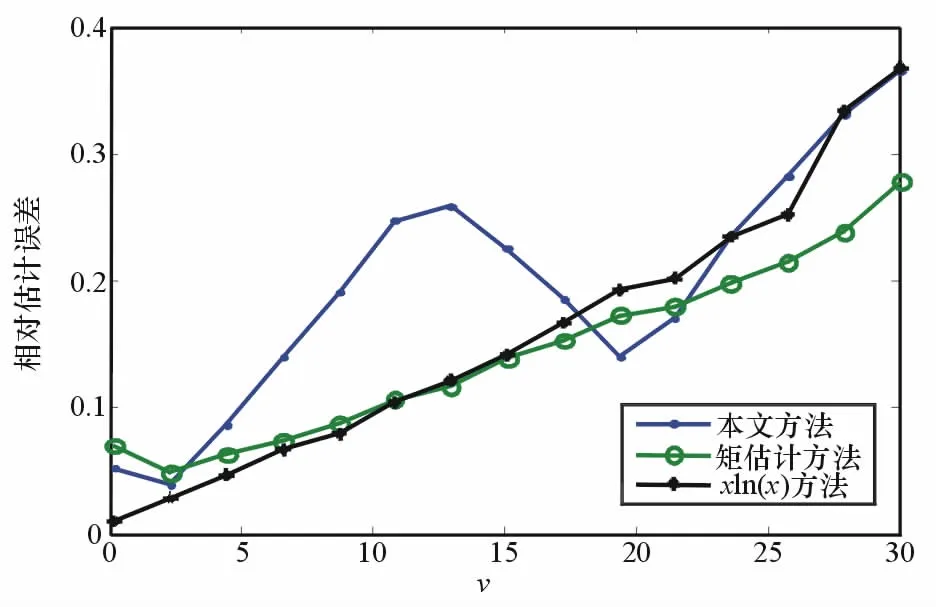
圖2 估計相對誤差

3 實測數據分析

為驗證本文方法的有效性，對169組不同距離單元的實測海雜波數據進行了分析。數據采集條件為：雷達距海面7m，H 極化，脈寬0.5μs，重頻5kHz，2級海情。圖3所示為第60距離單元的雜波幅度波形和功率譜密度，幅度分布直方圖如圖4所示，其分布特性偏右，形狀參數v較大。

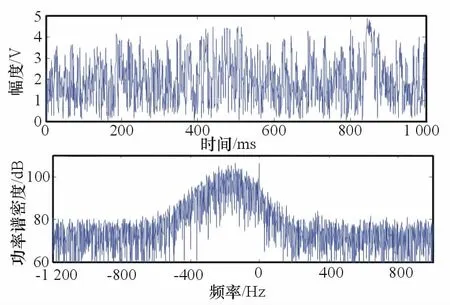
圖3 實測雜波數據時域頻率波形

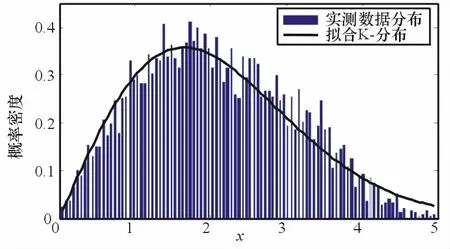
圖4 雜波幅度分布特性

采用不同方法對該組數據進行參數估計，結果列于表1中。可以看出，矩估計方法和xln（x）法對形狀參數的估計結果為負，為錯誤估計。而本文方法能夠給出了v和a的估計結果，按照該估計參數對數據進行K－分布擬合，結果如圖4所示。可以看出，擬合結果能夠很好地和實測數據相吻合。

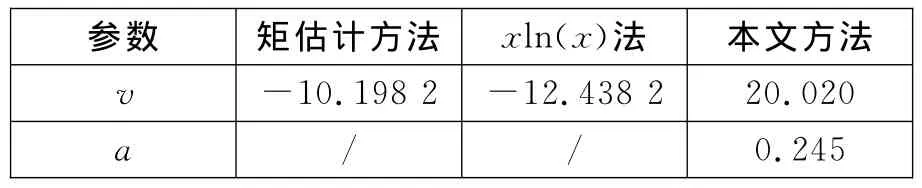
表1 雜波數據參數估計結果

對全部數據進行分析，統計有效估計次數和平均擬合誤差，擬合誤差的計算方法為：

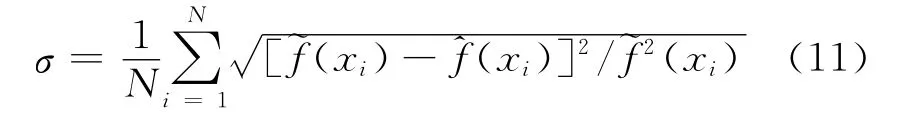
統計結果如表2所示。

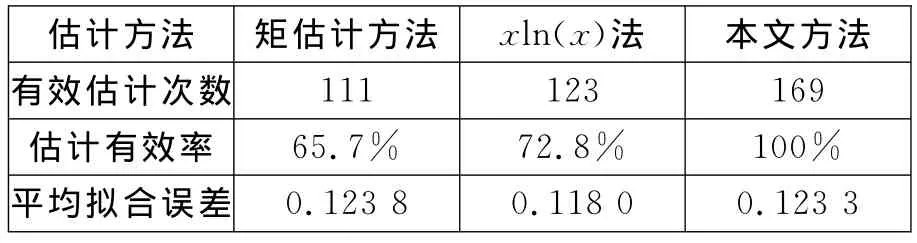
表2 數據處理結果

可以看出，矩估計方法和xln（x）法無法對全部數據進行有效估計，矩估計方法的估計有效率為65.7%，xln（x）法的估計有效率為72.8%；而本文方法對所有數據進行了有效擬合，平均擬合誤差介于xln（x）法和矩估計方法之間，能滿足工程要求。

4 結束語

本文利用ln（x）的一、二階矩之間的特定函數關系求解K－分布雜波的形狀參數和尺度參數，避免了常規方法在處理雜波數據時由于數據長度有限和噪聲所導致的錯誤估計的發生。利用該方法對不同形狀參數的K－分布數據進行了參數估計，結果表明該方法具有很高的估計有效率，利用實測海雜波數據對本文方法進行了處理，說明了本文方法具有很高的工程實用價值。

［1］Joughin I R，Percival D B，Winebrenner D P.Maximum likelihood estimation of K－distribution parameters for SAR data［J］.IEEE Transactions on Geosciences and Remote Sensing，1993，31（5）：989－999.

［2］Roberts W J J，Furui S.Maximum likelihood estimation of K－distribution parameters via the expectation maximization algorithm［J］.IEEE Transactions on Signal Processing，2000，48（12）：3303－3306.

［3］Wachowiak M P，Smol kov R，Zurada J M，Elmaghraby A S.Estimation of K distribution parameters using neural networks［J］.IEEE Transactions on Biomedical Engineering，2002，49（6）：617－620.

［4］Iskander D R，Zoubir A M.Estimation of the parameters of the K－distribution using higher order and fractional moments［J］.IEEE Transactions on AES，1999，35（4）：1453－1457.

［5］Raghavan R S.A method for estimating parameters of K－distributed clutter.［J］.IEEE Transactions on AES，1991，27（2）：238－246.

［6］Blacknell D，Tough R J A.Parameter estimation for the K－distribution based on［zlog（z）］［J］.IEE Proceedings－Radar，Sonar and Navigation，2001，148（6）：309－312.