基于積分的級數斂散性判別方法
2013-08-11 07:12:28朱智慧長江大學一年級教學工作部湖北荊州434025
長江大學學報(自科版) 2013年31期
朱智慧 (長江大學一年級教學工作部,湖北 荊州434025)
無窮級數與微積分是數學分析的2大基本內容,它們在方法和理論上是共同發展和成熟起來的,兩者都以極限為工具從收斂與發散2方面研究函數,在一般教材中積分的應用比較多談到的是幾何應用[1-3],而利用積分判定級數斂散性則很少提及。下面,筆者通過應用定積分與反常積分對級數斂散性的判定進行了探討。
1 級數與定積分
定義1 若函數f(x)在[a,b]上有界,在[a,b]中任意插入若干個分點:
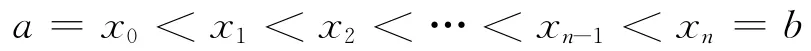
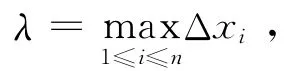

由定義1可以看出,定積分是積分和的極限,因此可對無窮級數前n項的和構成的數列極限問題轉化為定積分來解決。
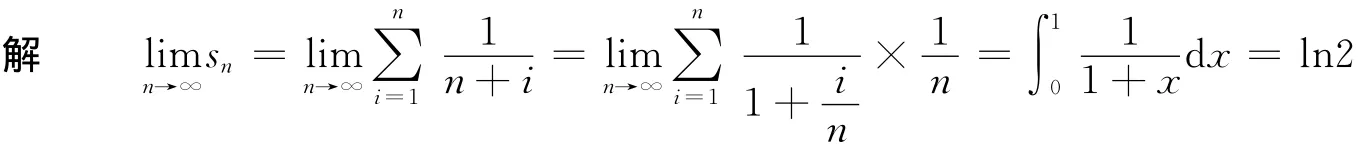
2 級數與反常積分
2.1 級數與無窮限反常積分
由數學分析中的歸結原則[1]可得以下定理:
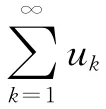
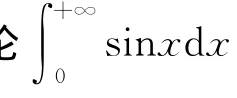
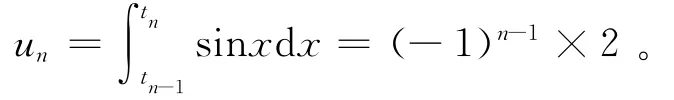
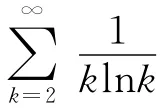
2.2 級數與無界函數的反常積分
3 結 語
在高等數學的學習過程中,可以通過一定條件下級數與積分的內在聯系,使得所遇級數問題與積分問題可以得到相互轉化,從而解決問題。同樣,在高等數學教學過程中,更加應該加強對知識點的串聯,從而培養學生知識的遷移能力,更好的掌握所學知識,達到知識的融會貫通。
[1]華東師范大學數學系 .數學分析 [M].北京:高等教育出版,1991.
[2]同濟大學數學系 .高等數學 [M].北京:高等教育出版,1978.
[3]陳傳璋 .數學分析 [M].第2版 .北京:高等教育出版社,1983.
猜你喜歡
海峽姐妹(2020年9期)2021-01-04 01:35:44
甘肅教育(2020年14期)2020-09-11 07:57:50
VOGUE服飾與美容(2020年9期)2020-09-02 14:47:26
甘肅教育(2020年12期)2020-04-13 06:25:34
東方教育(2017年19期)2017-12-05 15:14:48
唐山文學(2016年2期)2017-01-15 14:03:59
山東青年(2016年1期)2016-02-28 14:25:25
當代修辭學(2014年3期)2014-01-21 02:30:44
體育師友(2013年6期)2013-03-11 18:52:18
公務員文萃(2013年5期)2013-03-11 16:08:37

