基于時間序列模型預測汽車銷量研究
郭順生,王磊,黃琨
(武漢理工大學 機電工程學院,武漢 430070)
1 引言
2013 年初,中國汽車工業協會信息發布會在京召開。中國汽車工業協會副秘書長師建華發布了2012 年汽車市場運行情況概述及2013 年汽車市場形勢預測。數據顯示,2012 年全國汽車產銷1927.18 萬輛和1930.64 萬輛,同比分別增長4.6%和4.3%,比上年同期分別提高3.8和1.9個百分點。我國汽車的銷量再創新高,穩居全球產銷第一。
雖然我國2012 年的汽車銷售量很好,但是也的確暴露出了很多的問題。例如,很多制造商在上半年對于整個汽車銷售市場盲目樂觀,造成了2012 年汽車市場高庫存的局面,最后演變成了大打價格戰的結局,對整個汽車銷售市場產生了巨大沖擊和影響,這一教訓在制定2013 年汽車銷售目標時,能否吸取教訓還難說,能否客觀、冷靜、實際地制定2013 年計劃,也很難說。
汽車的銷量也就是汽車的增加量,可以準確地反映人們對汽車的需求。相比于以往文章中預測我國汽車市場的年銷售情況,本文引入時間序列模型,以月份為單位,對2013 年上半年整個中國汽車市場的月銷量進行了一個預測,這樣更有利于企業根據每個月份的預測結果快速地調整庫存以及整個供應鏈,從而更好地適應市場變化。
本文嘗試用自回歸移動平均模型(ARMA)通過Eviews軟件[1],建立我國汽車銷量預測模型,希望可以對企業在根據預測值進行產量和庫存安排的同時、及時地調整市場戰略提供一定的幫助。此外,政府相關部門在交通布局、道路整改、停車位增設、城市綠化等政策的制定上參照預測結果進行相應調整。
2 ARMA 模型概述
ARMA 模型全稱為自回歸移動平均模型(Auto-Regressive Moving Average Model,簡稱ARMA),是由Box和Jenkins 于1970 年代初提出的著名時間序列預測方法,又稱為box-jenkins 模型、博克思-詹金斯法[2]。ARMA 模型可分為三種類型:自回歸(AR:Auto-Regressive)模型、移動平均(MA:Moving-Average)模型和自回歸移動平均(ARMA:Auto-Regressive Moving-Average)模型[2]。
(1)AR 模型。時間序列用前期值和隨機項的線性函數表示,是系統對過去自身狀態的記憶。p階自回歸模型記為AR(p),其式為[3]:
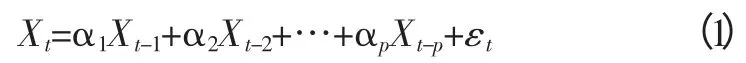
(2)MA 模型。用當期和前期的隨機誤差項的線性函數表示,是系統對過去時刻進入系統的噪聲(隨機擾動項)的記憶[3]。q階移動平均模型記為MA(q),其式為:
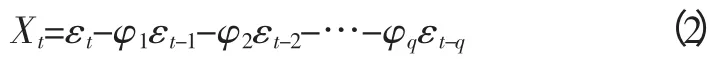
其中,εt為隨機擾動項。
(3)ARMA 模型。用當期和前期的隨機誤差項以及前期值的線性函數表示,是系統對過去自身狀態以及進入系統的噪聲的記憶[3,4]。ARMA(p,q)的形式為:
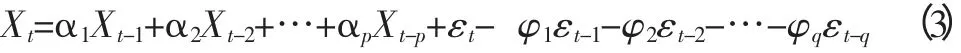
3 ARMA 模型的建立與檢驗
3.1 時間序列平穩性分析
集合ARMA 模型的使用條件,選用2009 年1 月到2012年12 月中國汽車月銷售量,見表1,構成時間序列{sh}。
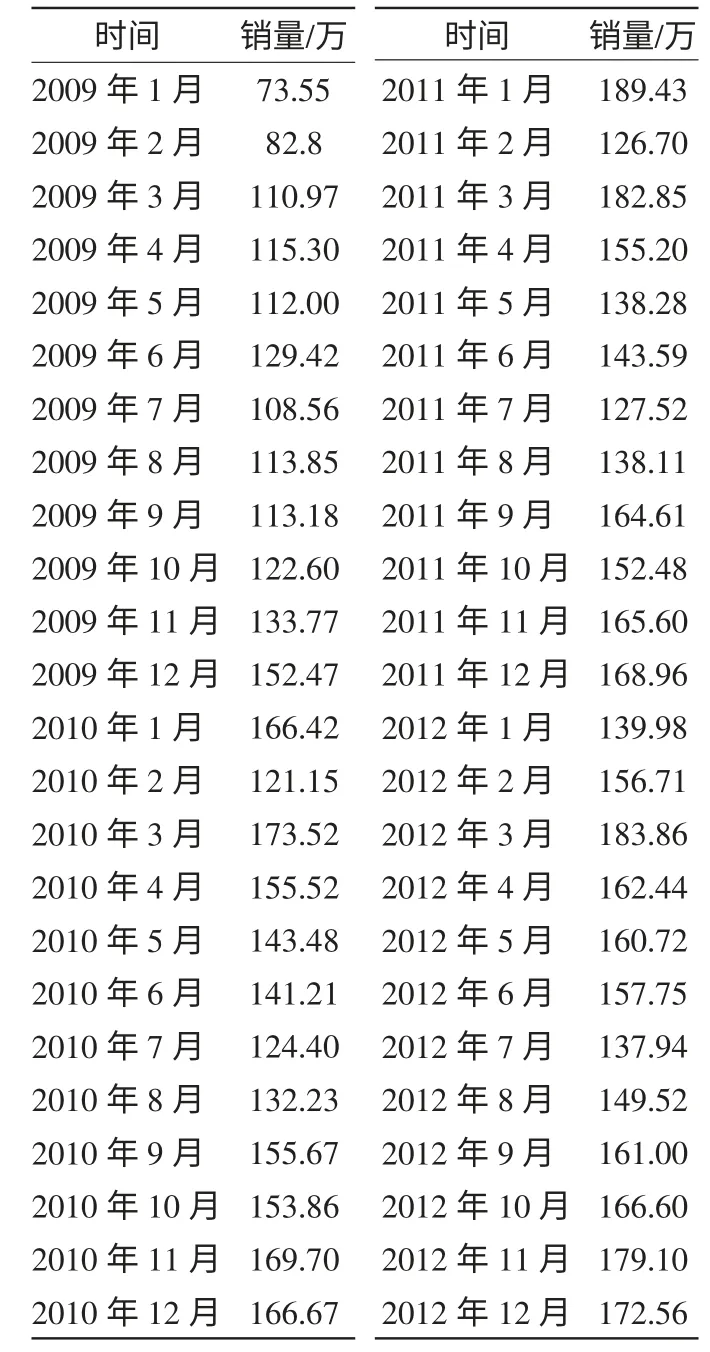
表1 2009 年1 月-2012 年12 月中國汽車月銷量
根據表1中的時間序列,做出中國汽車月銷售量時間序列圖(見圖1),由圖1 可以看出該序列自2010 年之后有明顯的季節性規律,每年的年初和年末,汽車銷售量都會較高,而年中則會比較低靡。并且在2 月份,由于過年放假的原因,汽車銷售市場也會冷淡,所以每年的前三個月波動會比較大。根據圖1,做出時間序列{sh}的自相關以及偏相關函數圖(圖2),由于序列的自相關系數不是很快地(如滯后期K=2,3)趨于零,即緩慢下降,表明序列是非平穩的。
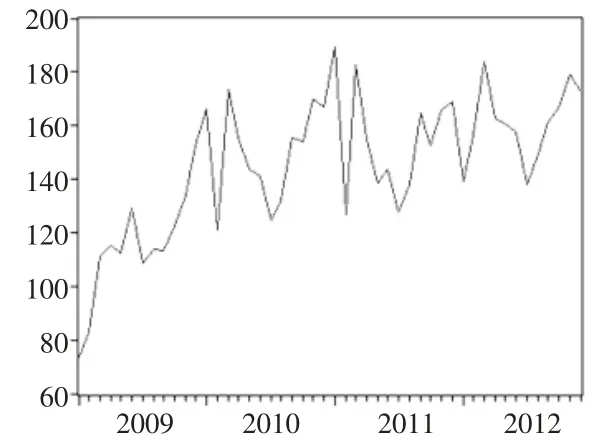
圖1 序列{sh}走勢圖
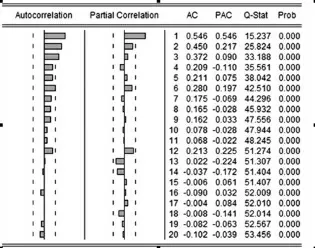
圖2 序列{sh}的自相關及偏相關分析
因非平穩序列{sh}存在異方差,且2009年的數據對于季節性很不明顯,因此除去2009 年,并對序列{sh}取 對 數做差分運算再進 行 ADF 檢驗,經過差分運算后,記時間序列為{sh1},該序列的自相關系數(圖3)很快地趨近于零,可初步表明該序列為平穩序列。
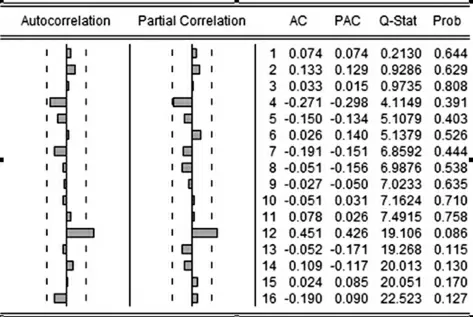
圖3 序列{sh1}的自相關及偏相關分析
將該序列進一步進行ADF 檢驗(表2),原假設為該序列存在單位根,而檢驗結果t 統計量值為-5.748626,低于顯著水平為1%的臨界值。這表明可以在99%的置信水平下不接受原假設,也就是該序列{sh1}不存在單位根,是平穩序列。

表2 序列{sh1}的ADF 檢驗
3.2 模型識別及定階以及檢驗
通過圖3 判斷,該序列在滯后期12 處的自相關系數和偏相關系數顯著異于零,因此可認為該序列存在一個周期為12的季節性變動。建立模型時,可在模型中加入周期為12的SAR 或SMA 項。
而AC 在滯后期k>4和PAC 在滯后期k>5 時出現結尾現象,具有ARMA 模型的特征,同時采用Akaike 提出的AIC 準則和Schwartz 提出的SC 準則,對序列{sh}的ARMA 模型進行逐步比較定階。當p=2,q=5 時,達到可以取得的最大值(R2=0.994596),AIC 與SC的一組值達到最小值(AIC=-5.912577,SC=-5.467391)。對該模型的殘差序列{ε1}進行自相關分析(圖4),由圖中可看出殘差序列的自相關系數都均勻的分布在置信區間內,并趨近于零,這表明該序列通過白噪聲檢驗。由上述分析可確定{sh} 適合ARMA(5,2)模型。

圖4 序列{εt}的自相關及偏相關分析
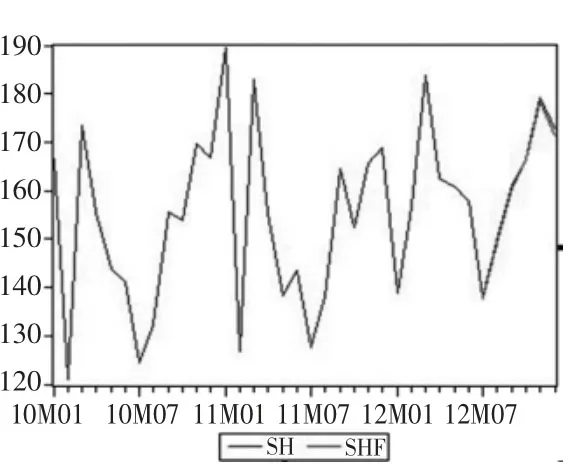
圖5 2012 年下半年預測結果與真實結果
3.3 模型的評估
利用該模型預測2012 年7 月 到2012 年12 月汽車月銷量,與真實值擬合(圖5,表3),由圖中可以看到預測結果與真實結果擬合度非常好,預測誤差也都控制在了3%以內,而預測結果的Theil 不等系數為0.002075,因此認為該模型預測在短期內具有較高的精度。
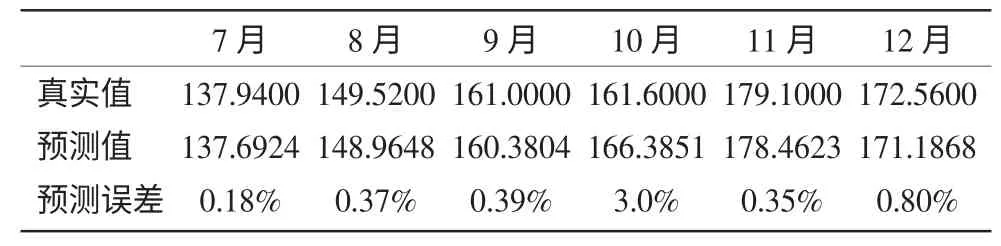
表3 2012 年下半年預測結果與真實結果
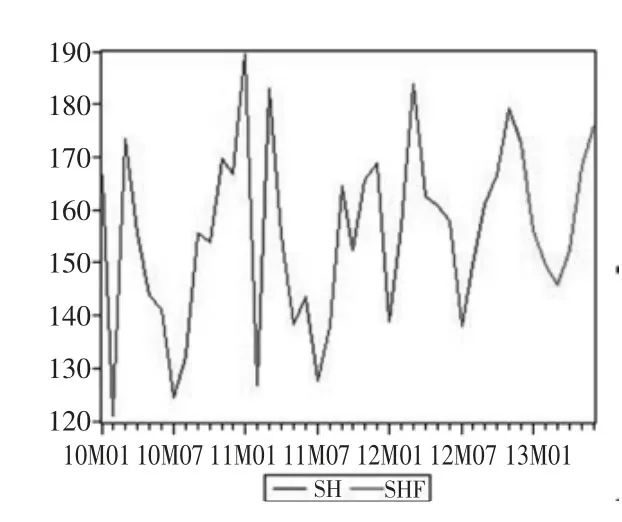
圖6 2013 年上半年預測結果
4 模型的預測
由于該模型在短期內具有較高的精度,且不利于長期預測,因此將擴展樣本至2013 年6 月,利用ARMA(5,2)模型,以及2009 年1 月到2012 年12 月的有關數據,對2013 年上半年汽車月銷量進行預測,結果如圖6、表4所示。

表4 2013 年上半年預測結果
5 結語
通過ARMA(5,2)模型預測的結果表明,2013 年上半年中國汽車銷量會有一個先降后升的趨勢,但是由于原時間序列較少,對預測精度是一個不利的影響,本次預測只考慮了歷年數據的變化趨勢,沒有考慮市場中一些隨機因素,如節能減排的壓力以及世界經濟的影響,求出的預測值只是一個大概值,因此筆者認為如果考慮將ARMA 模型與其他模型混合使用,同時考慮時間序列以及隨機因素并且增加樣本,那么應該優于此模型,并大大提高預測精度。
[1]李敏,陳勝可.Eviews 統計分析與應用[M].北京:電子工業出版社,2011:112-142.
[2]LIM C,et al.Forecasting h(m)otel guest nights in New Zealand[J].International Journal of Hospitality Management,2009(28):228-235.
[3]李根,趙金樓,蘇屹.基于ARMA 模型的世界集裝箱船手持訂單量預測研究[J].科技管理研究,2012(16):217-220.
[4]盧小麗,何光.基于ARMA 模型的四川省農村居民收入趨勢預測[J].中國農學通報,2012,28(5):110-114.

