深海聲速剖面結構變化對會聚區偏移特性的影響分析

莊益夫，張旭，劉艷

（中國人民解放軍91550部隊，遼寧 大連 116023）

聲速剖面反映了一定范圍海區的聲速垂直結構，對于水下聲傳播有重要影響。會聚現象是深海海洋中特有的聲傳播現象。當聲源和接收器都位于海洋近表層時，向深海中發出的聲波會再次折回海面，在間隔約60～70 km的海面附近形成寬度為3～4 km的較高聲強環帶狀區域，稱為會聚區（Urick，1983）。會聚區是深海中良好的聲信道，很多文獻中對會聚區聲傳播的理論特性進行了廣泛的研究（Urick， 1983；Brekhovskikh， 2003；張 仁 和 ，1980， 1982；Zhang et al， 1995；趙 申 東 等 ，2003），但目前對于聲速剖面結構變化對會聚區影響的認識仍不夠充分（張旭等，2010）。中國周邊海域幅員遼闊，海洋地理、氣象、水文特征復雜，海洋聲速場的區域性、季節性特征變化顯著。研究不同類型聲速剖面結構條件下的會聚區特性對于海洋工程和國防領域的應用具有重要意義。

中緯度海洋的聲速剖面大多是由混合層、主躍層和深海等溫層的“三層結構”構成（Urick，1983）。目前主要有兩類參數化模型可用于描述這種聲速剖面結構。第一類是基于一定數量聲速剖面樣本的經驗正交函數（EOF）模型，這種方法將一定數量的聲速剖面樣本序列分解成正交的時間向量和空間向量，只需要用前幾階函數就可以較為準確地重構序列中的任一剖面，大大減少了描述聲速垂直結構所需要的參數。LeBlanc等（1980）的研究表明，EOF是描述聲速剖面最有效的基函數，一些研究中已證明了這種方法的可行性（沈遠海等，1999；Peng et al，2003；何利 等，2006）。另一類模型是基于一系列數學表達式及系數的解析函數模型，比較典型的有Munk模型和GDEM模型。Munk（1974）根據實測深海密度結構的層化特征，提出了一種適用于中緯度深海海區的經典聲速剖面模型。這種指數表達式的描述方式適用于深海聲道型的剖面結構，在近幾十年的相關研究中被廣泛引用。Davis等（1986）提出了GDEM（Generalized Digital Environmental Model）模型，用更復雜的函數組合描述水溫和鹽度剖面，再利用經驗公式計算得到聲速剖面。Teague等（1990）曾證明，GDEM模型對不同海域的真實海洋環境具有廣泛的適用性。

然而，這幾種模型目前都存在著明顯的不足。EOF模型必須以一定數量的樣本作為基礎，且參數不具有直觀意義，無法通過調節參數對聲速剖面的結構形態進行控制。Munk模型對聲速剖面的描述過于理想化，對于真實海洋環境的描述誤差較大。GDEM模型雖具有廣泛的適用性，但由于需要通過先計算水溫和鹽度才能得到聲速剖面，使用的參數過多，且參數的直觀性不強。近期提出的分層聲速結構模型（LSSPM，Layered Sound Speed Profile Model）模型（張旭等，2011）用不同類型的函數分別描述混合層、主躍層、深海聲道層和深海等溫層，各層函數參數與聲速垂直結構有較好的對應關系，可實現對聲速剖面結構進行較好地控制。本文采用LSSPM模型對不同類型聲速剖面結構的典型變化引起的會聚區偏移特性進行研究。

1 分層聲速剖面模型（LSSPM）

對于“三層結構”的典型聲速剖面，LSSPM模型采用5個特征深度z0、z1、z2、z3、z4分別表示海面、混合層底、主躍層底、深海等溫層上邊界和海底的位置，根據4個水層不同的聲速結構特征建立擬合函數F（z）隨水深z的變化關系。這5個特征深度構成了聲速剖面各層的邊界： [z0，z1]為混合層， [z1，z2]為主躍層， [z2，z3]為深海聲道層， [z3，z4]為深海等溫層。假設深海聲道軸深度（剖面中聲速最小值所在深度）為zm，則zm∈ [z2，z3]。

對于混合層，聲速通常為正梯度結構，層中梯度值變化緩慢，擬合函數由二次多項式表示：

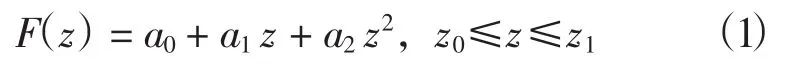
式中：a0、a1、a2為多項式系數。

對于主躍層，聲速為較強的負梯度結構，由GDEM模型中描述上層水溫剖面的冪函數形式表示：

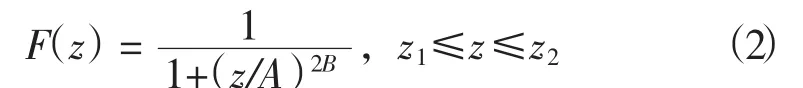
式中：系數A和B的意義與GDEM模型中的表達式相同（Davis，1986），A表征躍層的核心位置（聲速梯度極大值所在深度），B表征躍層核心位置附近的聲速梯度強弱。

對于深海聲道層，由Munk經典深海聲道模型的表達式描述：

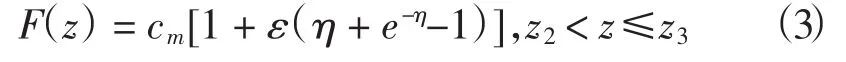
式中：η表示無量綱化的深度，η=2（z-zm）/D；zm和cm分別為聲道軸處的深度和聲速；D表示聲道厚度尺度；擾動系數ε=D·γA/2，其中γA為絕熱速度梯度（γA=0.011 4 km-1）。

對于深海等溫層，聲速為正梯度結構，梯度值變化緩慢，由二次多項式表示：

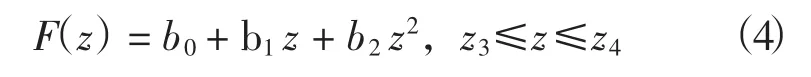
式中：b0、b1、b2為多項式系數。

分段函數建立之后，采用線性變換的方法使聲速剖面在4個水層的邊界處保持連續，將第i層擬合函數F（z）變換為聲速剖面函數c（z）的表達式為：

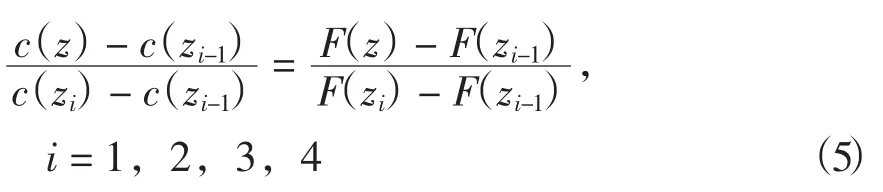
由式（1-5）構成的LSSPM模型共含有9個參數。在具體計算過程中，首先要根據聲速剖面樣本確定各特征深度的位置：z0和z4分別為海面和海底深度；混合層底深度z1可由近表層聲速極大值的位置確定；主躍層底的深度z2和深海等溫層上邊界的深度z3由深海聲道層來確定（文中取比聲道軸處聲速cm大5 m/s的聲速值作為參考聲速值cr，根據cr在深海聲道軸兩側限定的深度范圍確定z2和 z3的位置）。

2 結果分析

采用BELLHOP高斯束射線模型（Porter et al，1987）來計算聲場。傳統射線模型通常受到高頻近似的限制，而且不能有效計算焦散線附近的傳播損失。BELLHOP模型由Porter等提出，通過引入地聲學中的高斯近似方法較好地解決了聲線焦散對聲場計算的影響，在處理聲線能量焦散和完全影區等問題方面相對于傳統模型有明顯地改進，并且能夠適用于距離相關條件和復雜三維環境下的聲場計算（Bucker，1994；Weinberg et al，1996）。

在以下的分析中，首先根據LSSPM模型建立一個參考剖面（參數設置見表1），通過改變模型參數控制剖面的結構變化，進而討論這些變化對會聚區產生的影響。在計算聲場時聲源深度取20 m，頻率取1 kHz，采用半相干的方法計算傳播損失，根據傳播損失曲線遠場出現極大值的位置確定匯聚區距離（接收深度同聲源深度）。圖1給出了參考聲速剖面的結構及聲場示意圖。

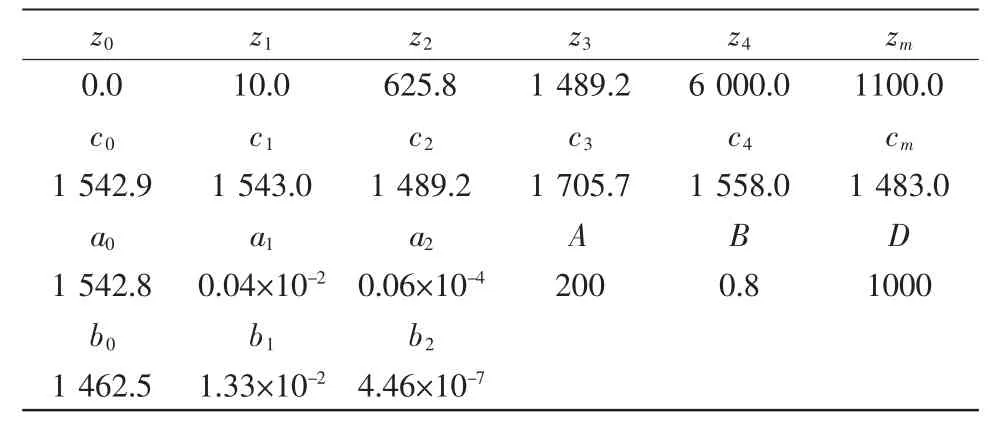
表1 基于LSSPM模型的典型中緯度聲速剖面的參數設置

2.1 聲速值變化的影響

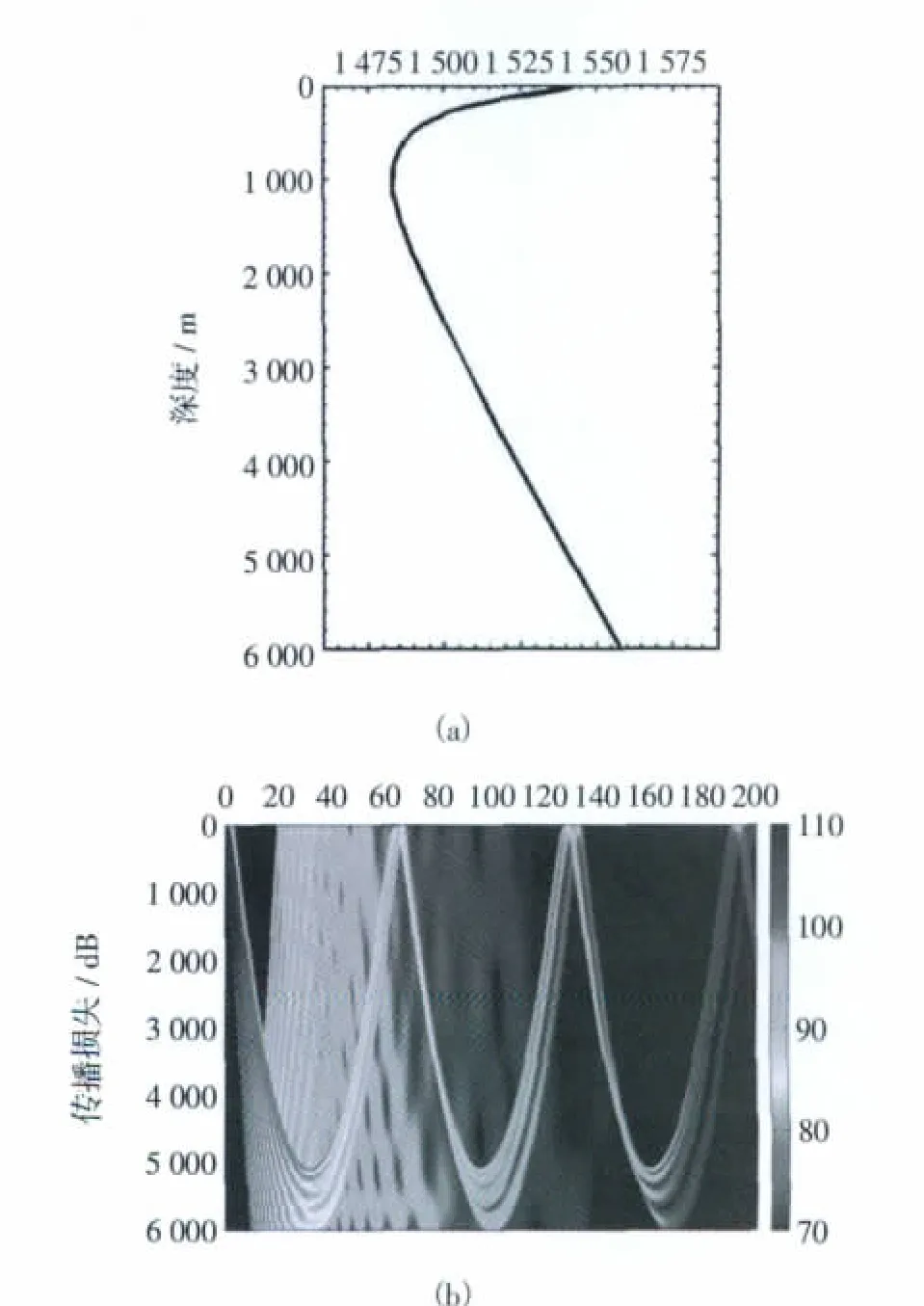
圖1 典型聲速剖面及傳播損失

首先考慮剖面聲速值整體變化（剖面各層聲速值同時增加）但聲速梯度保持不變的情況。表2給出了取±5 m·s-1和±10 m·s-1時會聚區的變化，圖2為聲速剖面及相應的傳播損失變化。根據表2，在聲速梯度不變的條件下，剖面聲速值每增加5m·s-1，第一會聚區向遠離聲源方向偏移0.1 km，第二、第三匯聚區的偏移量分別為0.2 km和0.3 km。可見，剖面的聲速值本身并不是會聚區發生偏移的主要原因。

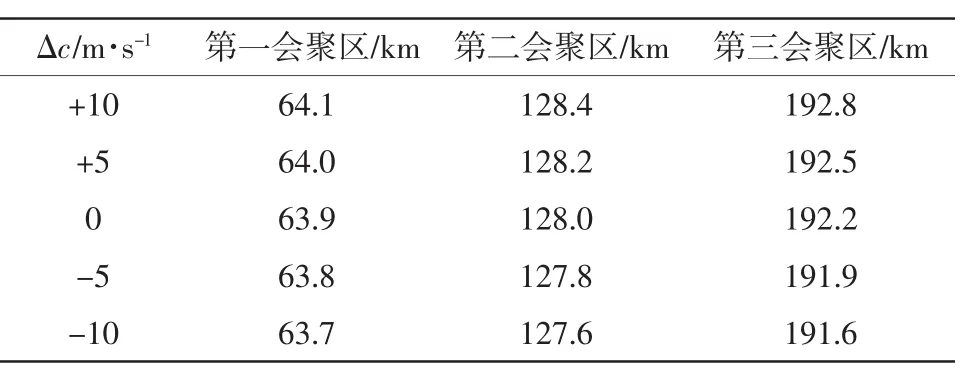
表2 聲速值平移引起的會聚區偏移

2.2 混合層變化的影響

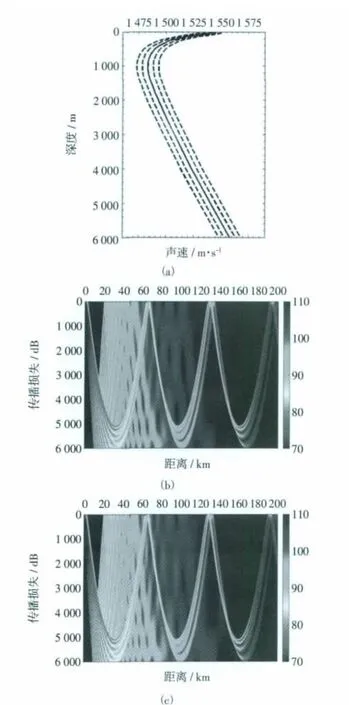
圖2 聲速值平移對應的剖面結構及傳播損失變化（b中Δc為10 m·s-1，c中為-10 m·s-1）

假設混合層的厚度發生變化，而混合層底的最大聲速值不變。這種情況描述了中、小尺度海洋現象伴隨的海-氣熱通量變化導致的混合層深度改變。表3給出了混合層厚度取10 m，50 m，100 m，150 m和200 m時會聚區的變化，圖3為聲速剖面及相應的傳播損失變化。根據表3，混合層每加深50 m，第一會聚區向遠離聲源方向偏移0.5～1.0 km，而第三匯聚區的偏移量可達2.0～3.0 km。隨著混合層的加深，伴隨有表面聲道的產生。然而，表面聲道與會聚區的偏移并無明顯關系，混合層加深引起的主躍層結構形態的變化是會聚區偏移的主要原因。

中緯度大洋海區的混合層通常具有明顯的季節性變化，夏季較淺，冬季較深，而其下的主躍層結構往往季節性變化較小。鑒于此，考慮另一種類型的混合層變化：假設主躍層的結構形態不變，而混合層隨聲速值的減小而加深。表4給出了混合層厚度取10 m，50 m，100 m，150 m和200 m時會聚區的變化，圖4為聲速剖面及相應的傳播損失變化。這種情況得到的結果與前一種假設條件下的結果剛好相反，混合層每加深50 m，第一會聚區向靠近聲源方向偏移1.0～2.0 km，第三匯聚區的偏移量約為2.0～4.0 km。這種情況雖未改變主躍層的結構形態，但卻改變了主躍層的強度。實際上，這兩種混合層變化的假設導致的會聚區偏移都是通過改變主躍層引起的。

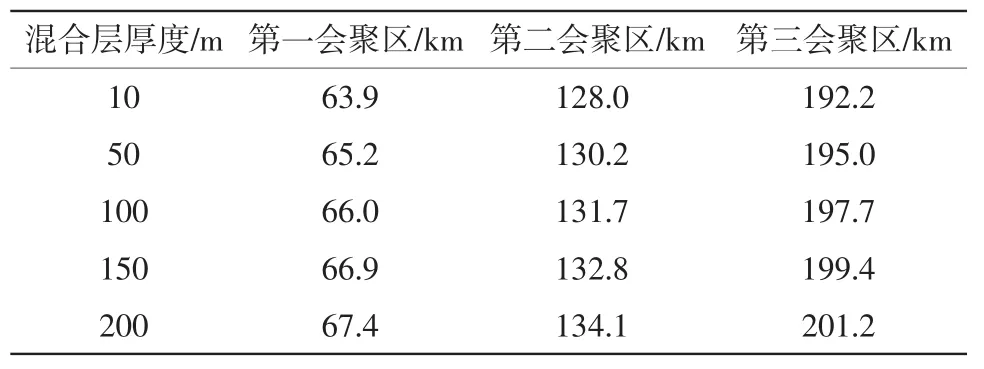
表3 混合層變化引起的會聚區偏移（假設條件1）

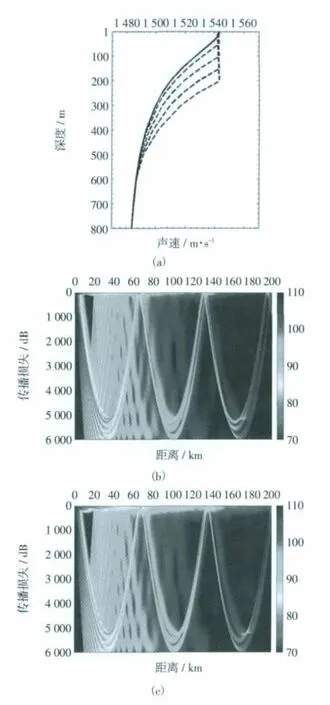
圖3 混合層變化對應的剖面結構及傳播損失變化（b中混合層為50 m，c中為200 m）

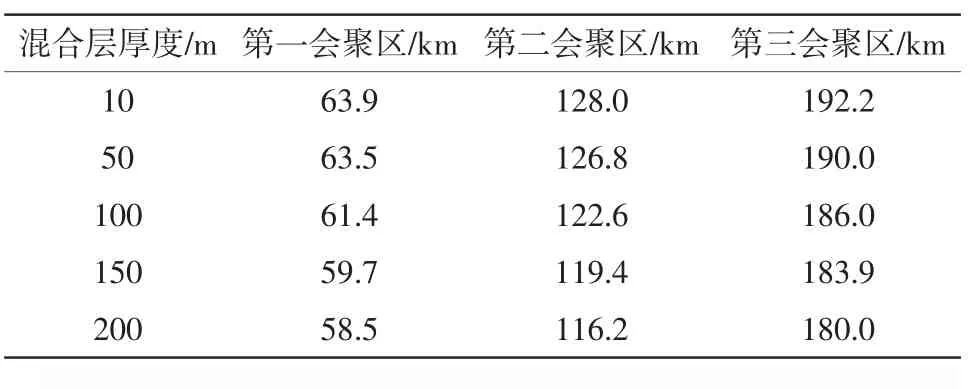
表4 混合層變化引起的會聚區偏移（假設條件2）

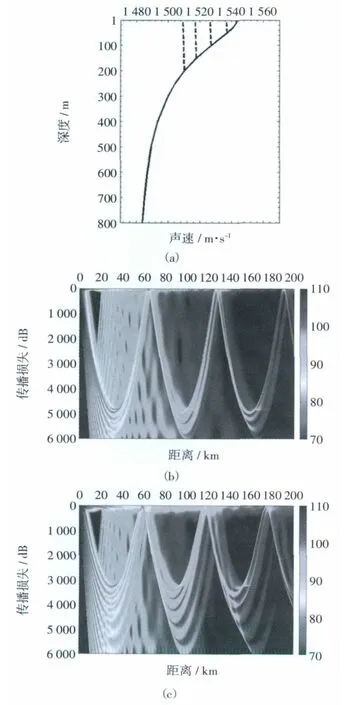
圖4 混合層變化對應的剖面結構及傳播損失變化（b中混合層為50 m，c中為200 m）

2.3 主躍層的影響

假設主躍層底的位置和聲速保持不變，主躍層強度以及形態結構隨近表層聲速的變化而變化。這種情況描述了不同緯度主躍層中的水團差異導致的聲速剖面變化。表5給出了近表層聲速極大值變化取±5 m·s-1和±10 m·s-1時會聚區的變化，圖5為聲速剖面及相應的傳播損失變化。根據表5，近表層聲速增加5 m·s-1（聲速梯度約增大0.01 s-1）使第一會聚區向遠離聲源方向偏移1.0～2.0 km，而第三會聚區的偏移量可達3.0～5.0 km。典型中緯度海區冬季與夏季的近表層聲速可相差15～20 m·s-1，這將使第一會聚區出現3～5 km的偏移。可見，主躍層的結構及變化對于會聚區聲傳播有重要影響。

表5和圖5表明，主躍層越強，會聚區的位置偏離聲源越遠。在近場，主躍層越強，聲線偏折越大，會聚區的位置應更靠近聲源而不是遠離聲源。然而，主躍層在引起近場聲線折射差異的同時，還會造成聲線進入深海等溫層時入射角度的不同。在近場折射較強的聲線進入深海等溫層時獲得了較大的入射角，因此在深海折回的過程中獲得了更大的水平位移。由于不同角度的聲線在深海的偏移差異在量值上大大超過了近場，使得較強的主躍層最終將會使會聚區偏向更遠的位置。由此可以進一步解釋圖3和圖4中的兩種情況：對于第一種情況，混合層的加深使主躍層受到了“壓縮”，其厚度減小，強度變大，因此會聚區向遠離聲源方向偏移；對于第二種情況，雖主躍層聲速梯度不變，但混合層的加深使近表層聲速和躍層厚度明顯減小，因此實際上躍層的整體躍變程度減小了，因此會聚區向靠近聲源方向偏移。

2.4 深海等溫層的影響

假設深海等溫層上界位于4 000 m，其上的聲速剖面結構保持不變，其下聲速值有所變化，但保持相同的聲速梯度。這種情況反映了不同類型的深海水團中溫、鹽特征值不同導致的聲速差異。表6給出了深海等溫層上界聲速變化取±2 m·s-1和±4 m·s-1時會聚區的變化，圖6為聲速剖面及相應的傳播損失變化。可見，深海等溫層聲速增加2 m·s-1（聲速梯度約增大0.001 s-1）使第一會聚區向靠近聲源方向偏移1.0～1.5 km，第三會聚區的偏移量約為2.0～3.0 km。根據前文的分析，聲速值的整體變化引起的會聚區偏移很小。因此，這種條件

下會聚區的偏移主要是由聲速剖面在深海聲道軸與深海等溫層上界之間的聲速梯度差異造成的。這種梯度差異在真實的海洋中是存在的，因為中層水與深層水之間的溫、鹽特征值的過渡需要經過一個很厚的水層。這種情況下環境變化對會聚區的影響類似于主躍層，但由于聲線向海面方向偏折，因此與主躍層引起的聲線偏折方向相反。

表5 主躍層變化引起的會聚區偏移

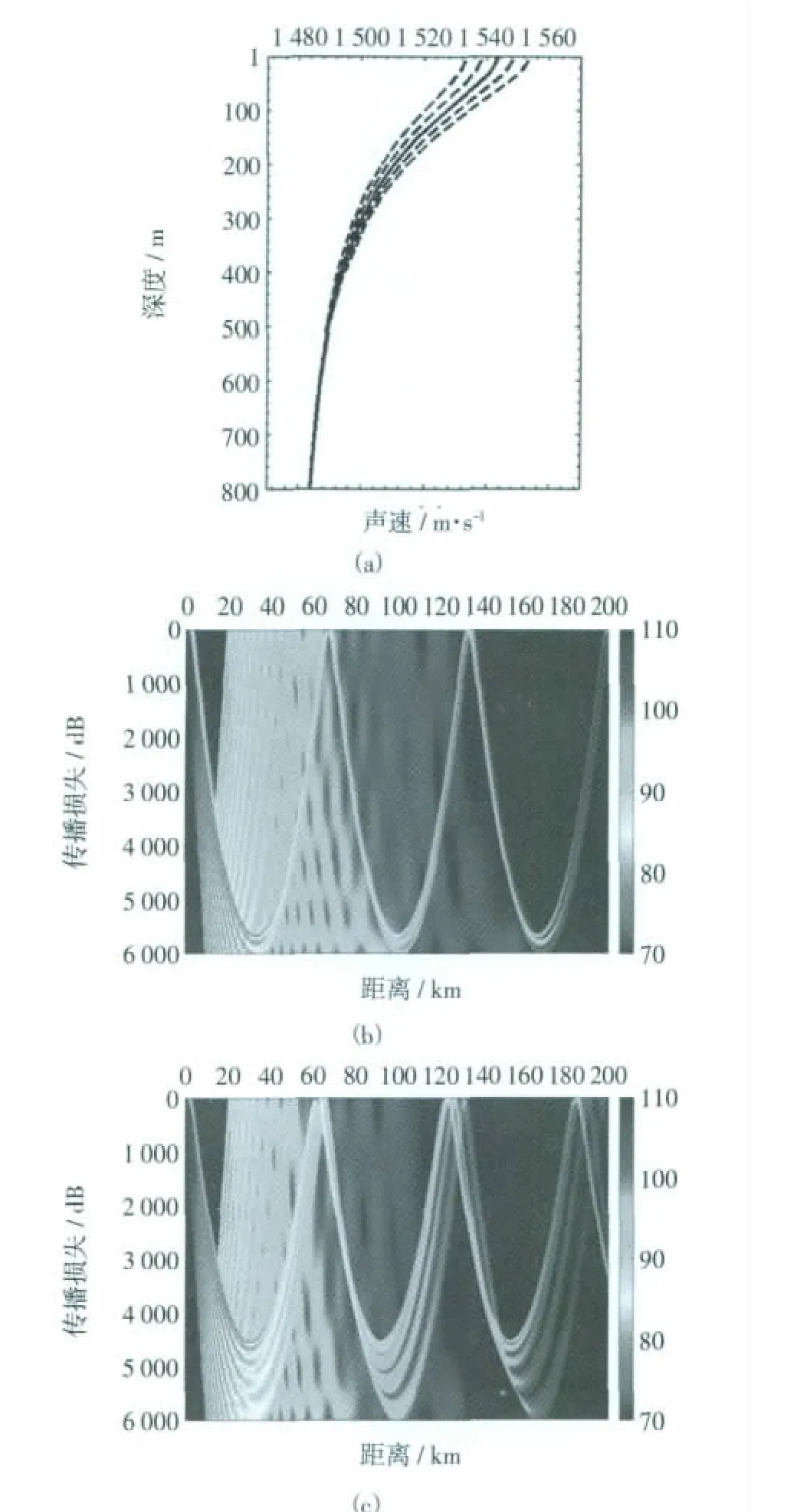
圖5 主躍層變化對應的剖面結構及傳播損失變化（b中為10 m·s-1，c中為-10m·s-1）

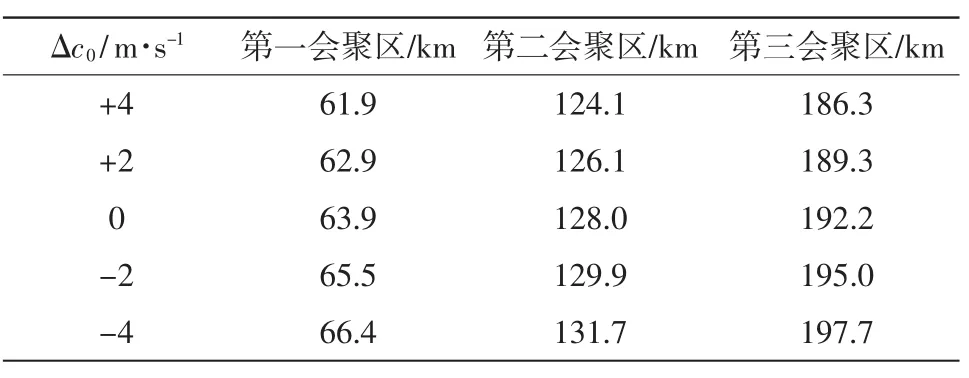
表6 深海等溫層聲速變化引起的會聚區偏移

圖6 深海等溫層變化對應的剖面結構及傳播損失變化（b中為4 m·s-1，c中為-4 m·s-1）

2.5 聲道軸的影響

假設主躍層下界與深海等溫層上界的聲速值相同，聲道軸處的聲速最小值發生變化。這種情況描述了不同類型的中層水侵入時引起的聲速變化。表7 給出了聲速最小值變化取±2 m·s-1和±4 m·s-1時會聚區的變化，圖7為聲速剖面及相應的傳播損失變化。可見，聲速最小值增加2 m·s-1使第一會聚區向遠離聲源方向偏移0.5～1.0 km，第三會聚區的偏移量約為1.0 km左右，這種變化小于深海等溫層上界以相同的聲速變化帶來的影響。實際上，聲道軸變化引起的會聚區的偏移是其上層水和下層水聲速梯度變化的綜合結果。若聲道軸處聲速最小值減小，則上層水的躍變強度變大，使聲線向下偏折的程度加強，同時下層水的正梯度也變大，使聲線向上折回的程度也變強，因此兩者產生的效應在一定程度上有所抵消，但由于上層影響更大一些，因此聲速最小值減小時引起的會聚區偏移與主躍層變強時的情況保持同相變化。

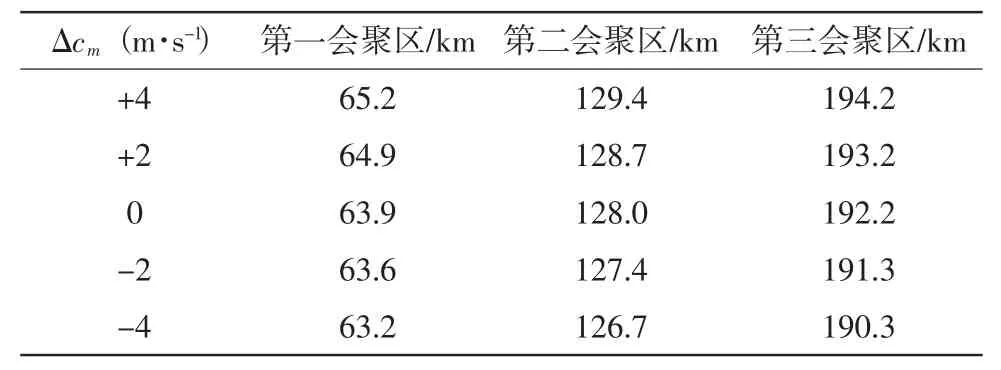
表7 聲道軸變化引起的會聚區偏移

3 結論

應用LSSPM模型得到了不同混合層、主躍層、聲道軸和深海等溫層結構類型的聲速剖面，通過對會聚區聲傳播的計算得出，聲速垂直結構的變化可導致會聚區位置出現不同程度的偏移。主要結論如下：

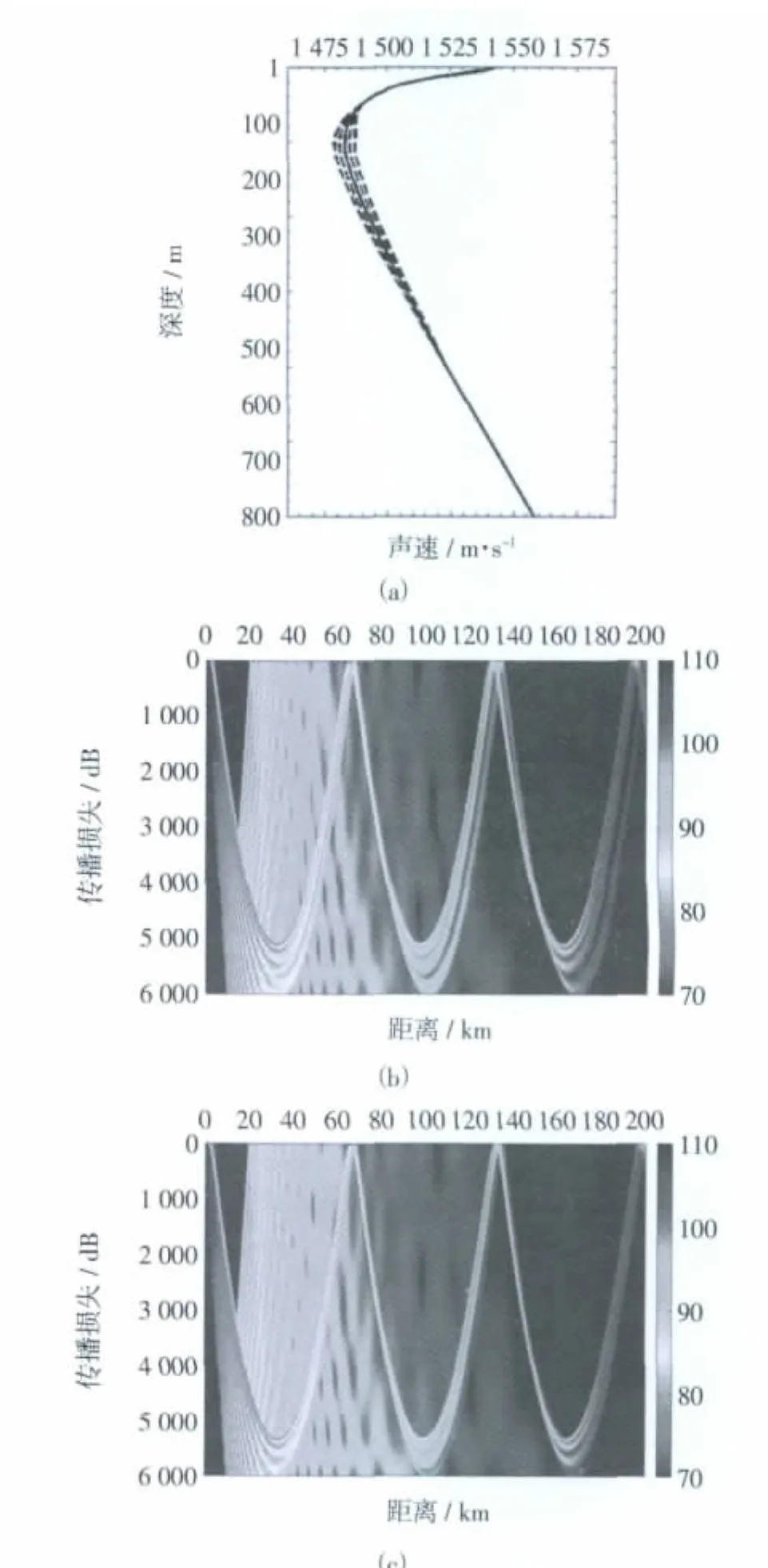
圖7 聲道軸聲速變化對應的剖面結構及傳播損失變化（b中為4 m·s-1，c中為-4 m·s-1）

（1）聲速值整體增大或減小引起的會聚區變化很小，5 m·s-1的聲速值變化造成的第一會聚區偏移僅為0.1 km左右。因此，造成會聚區聲傳播特征發生變化的不是聲速值本身，而是聲速剖面垂直梯度的變化。

（2）主躍層聲速結構受海洋上層水團配置的影響具有較大的季節性變化，這對于會聚區有較大影響。在主躍層中，躍層范圍內的聲速梯度差異引起的聲線偏折小于進入深海等溫層時掠射角差異引起的偏折。躍層增強使會聚區向遠離聲源的方向偏移，近表層聲速增加5 m·s-1（聲速梯度約增大0.01 s-1）使第一會聚區產生的偏移量約為1.0～2.0 km。

（3）混合層環境使聲場中出現的表面聲道對于會聚區的偏移沒有直接貢獻。混合層變化造成會聚區偏移的原因是伴隨的主躍層厚度及強度發生變化。對于近表層聲速不變的情況，混合層每加深50 m，第一會聚區向遠離聲源方向偏移0.5～1.0 km；對于主躍層結構不變的情況，混合層每加深50 m，第一會聚區向靠近聲源方向偏移1.0～2.0 km。

（4）深海等溫層的聲速變化體現了深海水團特性的差異，與主躍層引起的會聚區偏移呈反相變化。深海等溫層增加2 m·s-1（聲速梯度約增大0.001 s-1）使第一會聚區向靠近聲源方向偏移1.0～1.5 km。

（5）聲道軸附近的聲速變化反映了中層水團侵入并與本地水發生混合時的影響，引起的會聚區偏移是其上層水與下層水不同聲速梯度結構影響的綜合結果。聲速最小值增加2 m·s-1使第一會聚區向遠離聲源方向偏移0.5～1.0 km。

Brekhovskikh L M，Lysanov Yu P，2003.Fundamentals of ocean acoustics.3rd ed.New York：Springer-Verlag.

Bucker H P，1994.A simple 3-D Gaussian beam sound propagation model for shallow water.J Acoust Soc Am，95：2437-2440.

Davis T M，Countryman K A，Carron M J，1986.Tailored acoustic products utilizing the NAVOCEANO GDEM（a generalized digital environmental model）.In proceedings，36th Naval Symposium on Underwater Acoustics.San Diego：Naval Ocean Systems Center.

LeBlanc L R，Middleton F H，1980.An underwater acoustic sound velocity data model.J.Acoust Soc.Am，67：2055-2062.

Munk W H，1974.Sound channel in an exponentially stratified ocean，with application to SOFAR.J Acoust.Soc.Am，55（2）：220-226.

Peng L H，Wang L，Qiu X F，et al，2003.Modal wave number tomography for South China Sea front.China Ocean Engineering，17（2）：289-294.

Porter M B，Bucher H P，1987.Gaussian beam tracing for computing ocean acoustic fields.J.Acoust.Soc.Am，82，1349-1359.

Teague W J，Carron M J，Hogan P J，1990.A comparison between the Generalized Digital Environmental Model and Levitus Climatologies.J.Geophys.Res，95：7167-7183.

Urick R J，1983.Principles of underwater sound.3rd ed.New York：Mc－Graw-Hill.

Weinberg H，Keenan R E，1996.Gaussian ray bundles for modeling highfrequency propagation loss under shallow-water conditions.J.A－coust.Soc.Am，100：1421-1996.

Zhang R H，HE Y，LIU H，1995.Applications of the WKBZ adiabatic mode approach to sound propagation in the Philippine sea.Journal of Sound and Vibration，184（3）：439-451.

何利，李整林，張仁和，等，2006.東中國海聲速剖面的經驗正交函數表示與匹配場反演.自然科學進展，16（3）：351-355.

沈遠海，馬遠良，屠慶平，等，1999.淺水聲速剖面用經驗正交函數（EOF）表示的可行性研究.應用聲學，18（2）：21-25.

張仁和，1980.水下聲道中的反轉點會聚區（I）簡正波理論.聲學學報，1：28-42.

張仁和，1982.水下聲道中的反轉點會聚區（Ⅱ）廣義射線理論.聲學學報，2：75-87.

張旭，張永剛，2010.聲速垂直結構變化引起的匯聚區偏移.海洋科學進展，28（3）：311-317.

張旭，張永剛，張健雪，等，2011.一種新的聲速剖面結構參數化方法.海洋學報，33（5）：54-60.

趙申東，宋志杰，趙海彬，2003.穿越深海會聚區的聲源定位方法研究.應用聲學，4：35-39.