基于問題結構的邊界啟發式方法

李占山，張 良，郭勁松，張 乾

（1.吉林大學 符號計算與知識工程教育部重點實驗室，長春 130012；2.吉林大學 計算機科學與技術學院，長春 130012）

0 引 言

約束滿足問題（Constraint satisfaction problems，CSP）是人工智能方向的一個重要分支，相關技術被廣泛應用于組合問題求解，如配置器設計、調度、符號推理和路由等。相容性算法和求解技術的研究一直是CSP領域的研究熱點，國內研究人員已有工作主要集中于前者［1－4］，而隨著約束滿足問題應用領域的不斷擴大，約束求解技術得到了越來越多的關注。已有求解算法主要包括三類:回溯算法、局部搜索和動態規劃［5］。作為一種完全求解算法，回溯算法的主要任務包括為可解問題找到解以及證明不可滿足問題的不可解性，但在應用過程中，由于問題解空間規模較大，經常會出現“組合爆炸”現象，樸素回溯過程在人們期望的時間內難以給出一個有效解，如何提高求解效率成為研究回溯算法面臨的首要問題。

求解過程中，回溯算法進行深度優先檢索，需要不斷選擇變量來進行實例化，對眾多問題的實驗研究表明，變量被實例化的順序對于能否高效地求解起著至關重要的作用。為了得到好的搜索變量排序，研究人員提出了多種變量啟發式方法，對于已有啟發式的討論可參見文獻［5］。通過實驗對比研究人員發現，沒有一種現有啟發式能在所有問題上的求解效率明顯優于其他方法。因此，根據問題自身特性，尋找基于問題結構的啟發式方法被認為是提升求解效率的有效途徑。

Composed問題為一類隨機問題，眾多實際應用問題具有類似于Composed問題的結構特性，但受限于問題的特殊結構，現有啟發式方法在處理該類問題時總是生成過多節點，造成求解效率下降。本文從Composed問題結構出發，提出邊界變量集的概念，并給出了Composed問題中邊界變量的篩選方法，在此基礎之上設計實現了邊界啟發式方法。

1 問題背景

定義1 二元約束網絡G＝ （X，D，C），其中，X 為有限變量集｛X1，X2，…，Xn｝，D 為論域集｛D1，D2，…，Dn｝，對于任意變量Xi∈ X，Di為其所有可能取值構成的有限論域，即Di＝dom（Xi），C 為有限約束集｛C1，C2，…，Ce｝，任意Ci∈C均為作用在X上的二元關系。

變量Xi和Xj之間的約束記為Rij，則Rij?dom（Xi）×dom（Xj），值對（（Xi，a），（Xj，b））滿足Rij，當且僅當（（Xi，a）（Xj，b））∈Rij。約束網絡中，若變量Xi和Xj之間存在約束，則變量節點Xi和Xj之間存在弧（i，j），變量的度為與其相連約束弧的個數。

對集合X中所有變量進行賦值，令Xi＝ai，且ai∈Di，若元組T ＝ （a1，a2，…，an）滿足C中所有約束，則T為問題的一個解，如果T不存在，該問題是不可滿足的。對變量集X中任意k（1≤k＜n）個變量進行賦值，得到元組T1＝ （a1，a2，…，ak），若T1滿足C中所有約束，則稱T1為該問題的部分解。

約束網絡結構特征描述還需要使用到如下定義，詳細介紹可參考文獻［6］。

定義2 （松緊度Tightness）

約束弧 （i，j）的松緊度記為Tij，則

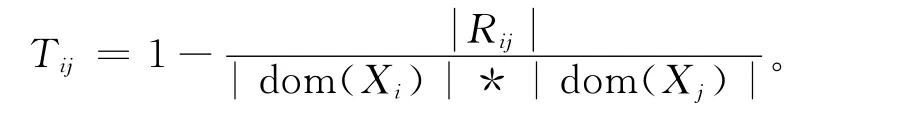
定義3 （網絡密度Density）

回溯求解過程中，為了壓縮搜索空間，基于約束傳播思想，每次變量賦值以后都要進行相容性檢查，如果檢查失敗，則需進行回溯，檢查成功則在當前未賦值變量中選擇變量進行實例化，變量啟發式則作用于該過程指導變量的選取。根據不同的相容性強度，研究人員提出多種求解算法，Maintain arc consistency（MAC）［7］算法是應用最為廣泛、被認為是效率較高的求解算法之一。下面給出弧相容定義以及MAC算法實現框架［8］:

定義4 （弧相容Arc Consistency）AC

（1）弧 （i，j）是相容的，當且僅當對任意（Xi，a）∈ dom（Xi），存在（Xj，b）∈dom（Xj），使得（（Xi，a），（Xj，b））∈Rij。

（2）約束網絡是弧相容的，當且僅當對任意弧（i，j）∈G，（i，j）是相容的。

MAC算法實現框架如下所示:

2 Composed問題

Composed問題在文獻［9］中首先被描述，結構上Composed問題具有多個局部區域，一般Composed問題結構如圖1［6］所示。

圖1 典型Composed問題結構圖Fig.1 Typical tructure of Composed problems

圖1為同一問題的兩個結構圖，左邊約束網絡任意約束弧灰度相同，而右側網絡中，約束弧灰度正比于其松緊度大小。一個Composed問題可表示成如下形式元組:

n1為中心區域變量個數，d1為中心區域變量論域的大小，m1為中心區域約束網絡密度，t1為中心區域內約束弧松緊度；s為伴隨區域個數；參數n2、d2、m2和t2表示伴隨區域局部網絡特性，所表示內容與中心區域相對應；L表示將一個伴隨區域連接到中心區域的約束個數，t3為約束松緊度。實驗部分所用測試樣例中，變量論域大小都為10，且每個伴隨區域都由8個變量構成，為了表示起來更加簡潔，略去某些特性，記為如下元組:

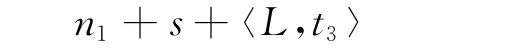
Composed問題中，伴隨區域局部網絡密度以及變量間約束弧的松緊度都要高于中心區域，直觀上來看，在伴隨區域找到一個滿足所有約束的部分解會更加困難，按照設計現有啟發式方法所依賴的失敗優先原則［10］，應該利用啟發式方法將求解過程引導到這些區域，但受限于問題結構，現有啟發式方法無法實現該目標。

常用啟發式方法中，deg和ddeg為靜態啟發式，dom／deg、dom／ddeg和dom／wdeg為動態啟發式，初始階段，兩類啟發式受到變量度的影響，選取變量都會落到中心區域。不同于其他啟發式，dom／wdeg方法為每個約束弧綁定動態weight值，變量Xi的wdeg值計算公式如下:

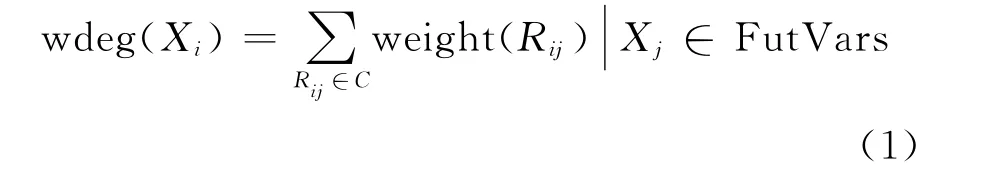
式中:FutVars為當前未實例化變量集。

當發生回溯時，導致死節點生成的約束弧weight值增加，當檢索過程進行到一定程度時，較大的weight值能幫助檢索過程跳轉到更加合理的區域進行。因此dom／wdeg啟發式具有一定學習能力，但該過程仍會生成過多節點，使得問題求解效率受到影響。

3 邊界啟發式方法

Composed問題在結構上可劃分為多個局部區域，當位于某個局部區域內部的變量被實例化并進行相容性檢查時，約束傳播沿著約束弧進行，而與該變量直接相連的變量大都位于該局部區域，這也使得整個約束傳播過程通常會被局限于該區域，dom／wdeg啟發式只能在該區域內收集啟發式信息，文獻［11］的分析表明，在更全面的解空間內收集啟發式信息有助于選擇更加合理的變量。

結合以上分析發現，Composed問題的求解關鍵為位于中心區域與伴隨區域相鄰邊界上的變量，即位于伴隨區域且通過弱約束與中心區域相連的變量，符合這樣條件的變量稱為邊界變量，由這些變量構成的集合稱為邊界變量集。當邊界變量被實例化并進行相容性檢查時，約束傳播會沿著約束弧同時影響到中心區域和伴隨區域，避免了被局限于某個區域。

邊界啟發式方法主要設計思想為從約束網絡中篩選出所有邊界變量構成邊界變量集，檢索過程中，邊界變量集中的變量應當具有高于其他變量的實例化優先級。為了找出邊界變量，在Composed問題約束網絡上首先給出如下定義:

定義5 （平均松緊度Average tightness）

定義6 （強約束，弱約束）

約束Rij為強約束，當且僅當Tij≥avg＿t；反之，若Tij＜avg＿t則Rij為弱約束。

邊界啟發式方法在實現時分為兩個階段，一是預處理階段，對變量進行篩選得到邊界變量集；二是在檢索過程中利用已有信息來選擇變量。

預處理階段，首先計算出網絡平均松緊度avg＿t，然后為變量設置標識數組strong［n］和weak［n］（n為變量個數），對任意i∈（0…n－1），如果strong［i］為真，則變量Xi有強約束連接，為假則不受強約束限制，如果weak［i］為真，則變量Xi有弱約束連接，為假則不受弱約束限制。遍歷C中元素，對任意t∈（0…e－1），若Ct為強約束，則將其所約束變量i和j的strong標識設為真，如果為弱約束，則將weak標識設為真。對strong和weak初始化結束之后，對任意變量Xi∈X，若其對應的標識strong［i］與weak［i］合取為真，則變量Xi為邊界變量，否則不是。這樣在預處理階段結束后就可以得到邊界變量集mid＿var＿set。

求解階段:給出邊界啟發式的兩種實現策略，記為H1、H2。H1:選擇變量時先要判斷 mid＿var＿set是否為空，不為空，按照dom／wdeg啟發式從mid＿var＿set中選擇一個變量；若為空，則在所有未賦值變量中按照dom／wdeg啟發式選擇變量進行實例化。H2:將mid＿var＿set內所有邊界變量的初始wdeg值設定為一個大于0的定值，以此來提高邊界變量在dom／wdeg啟發式下的實例化優先級，檢索過程按照dom／wdeg啟發式進行。兩種策略主要區別在于:前者只有在所有邊界變量被實例化以后才會選擇非邊界變量進行賦值，后者則是將dom／wdeg啟發式下的求解過程向邊界變量集靠攏，不保證邊界變量總是先于非邊界變量被選擇。

4 實驗結果及分析

實驗部分采用 MAC3rm［12］作為求解算法，MAC3rm為MAC算法中的一種，已有實驗結果表明，MAC3rm的實際求解效率要優于其他MAC算法。現有啟發式中，dom／wdeg［13］方法在一系列問題上有較好的表現，而且通過應用該啟發式，MAC算法可以有效地代替基于回跳的求解技術，成為較為穩定高效的通用求解算法，因此采用dom／wdeg啟發式與新啟發式方法進行對比，以求解所消耗CPU時間、檢索過程生成節點數以及約束檢查數作為參考標準，其中CPU時間t以ms為單位，生成節點數和約束檢查次數分別記為num和cc，這里一次約束檢查是指判斷一個值對 （（Xi，a），（Xj，b））是否滿足Rij所需要進行的操作。為了提高實驗本身的效率，預處理階段，首先在約束網絡上進行一次弧相容檢查，刪除變量論域中的不滿足值，該過程所進行的約束檢查次數不會被計入對比實驗數據。H2啟發式需要為每個變量對應wdeg設定初值，如果wdeg初值設為正無窮，則H2啟發式等同于H1，如果為0，則為dom／wdeg啟發式，為了避免該初值過大或者過小，并且能夠一定程度上反映問題規模，這里設定為n／2（n為變量個數）。

實驗中部分測試樣例的XML描述文檔可在線下載［14］，其他樣例則按照參數要求隨機生成，測試樣例包括了22組可滿足問題，每組問題都包括10個隨機生成的具體問題，其中14組為可滿足，8組為不可滿足樣例。為了避免單個問題本身特性對啟發式方法效果的影響，對每一類問題的10個樣例測試結果取其平均值進行比較。實驗結果如表1和表2所示。

實驗結果顯示H1啟發式在某些樣例上求解效率急劇下降，消耗時間和生成節點數都有數量級上的增加，表3給出其中一個樣例的結果對比。

對檢索過程中變量被實例化的順序和次數進行分析，可以發現產生這種現象的原因在于啟發式H1限制了dom／wdeg啟發式執行，使得即使收集到足夠多的啟發式信息，也不能正確跳離當前檢索區域。邊界變量位于不同伴隨區域內，在某個邊界變量被實例化且進行約束傳播之后，受dom／wdeg啟發式的影響，通常與該變量位于同一伴隨區域內的其他邊界變量會被選擇進行實例化。當該伴隨區域內所有邊界變量均被實例化后，受H1啟發式限制，檢索過程會跳轉到另外一個伴隨區域，并從中選擇邊界變量進行實例化。在Composed問題中，任意兩個伴隨區域之間沒有約束直接相連，因此在起始階段，各個伴隨區域內邊界變量較容易被實例化，但隨著被實例化邊界變量的增多，在相容性檢查時，中心區域內變量論域會被不斷刪減，此時可能出現論域為空的現象而產生回溯。對于某些樣例，只有當邊界變量集內大部分變量被實例化后才會發生回溯，這時H1啟發式會不斷調整邊界變量的取值，直到找到一個可拓展為最終解的部分解，由于邊界變量集本身檢索空間也很龐大，該過程會耗費大量時間。從實驗結果可以看到H1啟發式求解效率的這種波動現象只出現在了具有10個伴隨區域的問題類中，伴隨區域個數為5的樣例中沒有出現該現象，由于伴隨區域個數的減少，邊界變量集中變量數也相應減小，其自身搜索空間也不會過于龐大，因此規模較小的邊界變量集可以有效地避免出現這種情況。統計實驗數據時，為了能對三種啟發式方法在普遍問題上的求解效率進行對比，出現

這種現象的特殊樣例并沒有包括在內，表中對于包含這些樣例的每一類問題均注明了實際統計樣例的個數。

表1 可滿足問題Table 1 Satisfiable problems

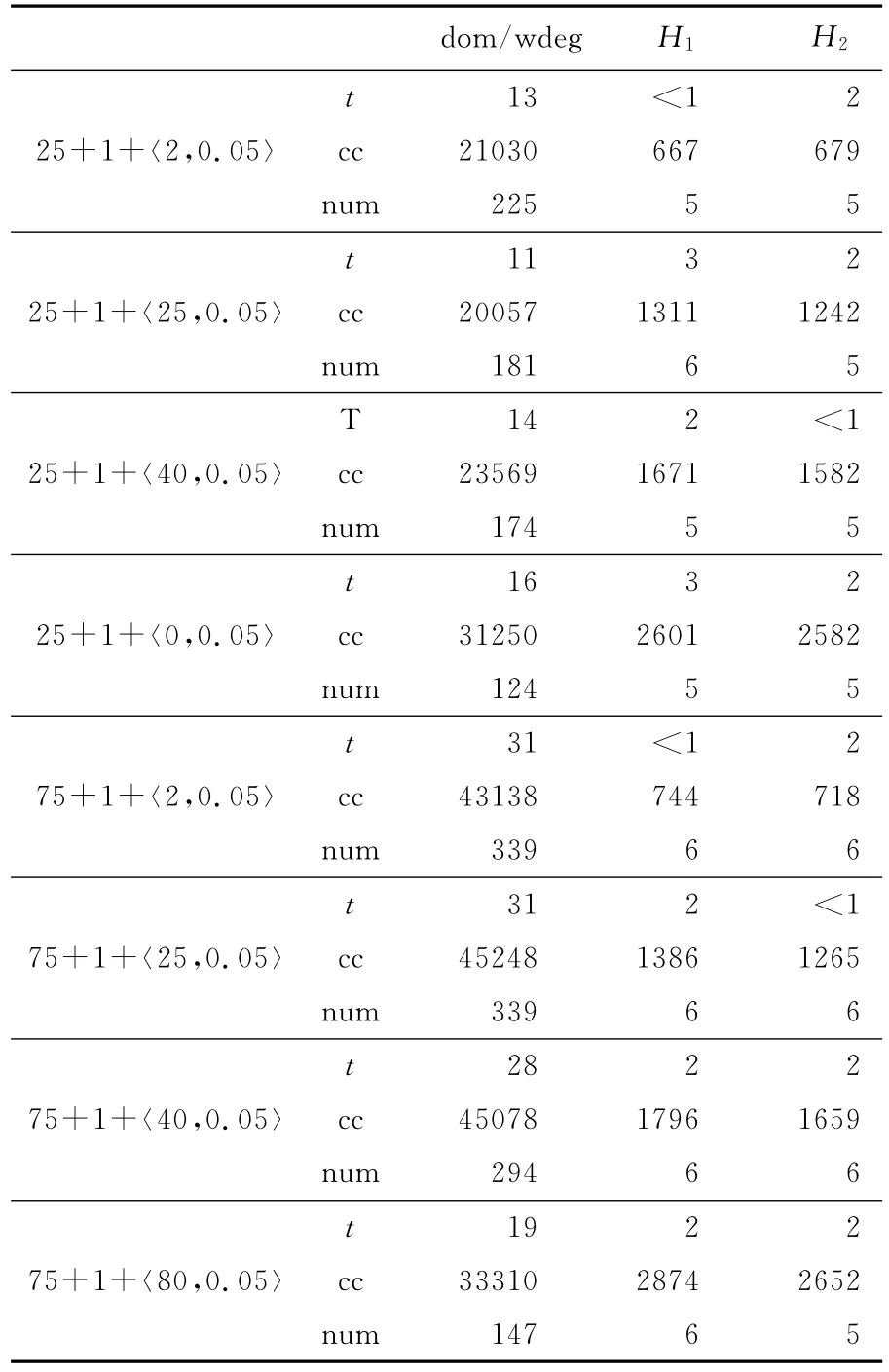
表2 不可滿足問題Table 2 Unsatisfiable problems

表3 特殊樣例Table 3 Abnormal instance

在所有可滿足問題中，25＋10＋〈5，0.05〉、75＋5＋〈10，0.05〉和75＋5＋〈15，0.05〉三類問題難度較小，三種啟發式方法在所有樣例上都接近于無回溯求解。而在其他可滿足問題上，H1和H2啟發式的求解效率均要明顯優于dom／wdeg啟發式。結合前面的分析，H1啟發式求解效率在某些問題上存在較大波動，不能夠實現穩定求解，而H2啟發式則在所有問題上都可以實現穩定高效的求解。H1和H2啟發式在一般問題上的求解效率相近，但由于穩定性差異，H2啟發式要比H1更適用于可滿足問題的求解。

在不可滿足問題上，H1和H2啟發式的求解效率都要遠高于dom／wdeg啟發式，啟發式生效的主要原因在于兩者為檢索過程尋找到了合適的起始點。在所有不可滿足樣例中，伴隨區域都是不可滿足的，通過對檢索過程中生成節點對應的實例化變量進行分析，發現dom／wdeg啟發式生成的多余節點大都對應中心區域內變量，只有在dom／wdeg啟發式收集到足夠信息時，檢索過程才能跳轉到邊界區域內變量，從而快速得出問題的不可滿足性。

通過對三種啟發式方法在可滿足問題和不可滿足問題上的求解效率進行對比，H1和H2啟發式要明顯優于dom／wdeg啟發式，其中H2啟發式方法在求解的穩定性上要好于H1啟發式。而邊界啟發式方法生效的原因主要有以下兩點:①啟發式篩選出的邊界變量位于問題求解困難的部分，滿足失敗優先原則，為檢索過程選擇了合適的起始點；②可以更好地發揮相容性技術在檢索過程中所能起到的作用，邊界變量賦值之后進行相容性檢查時，約束傳播會同時朝著伴隨區域和中心區域兩個方向進行，避免了被局限于某個局部，不僅可以壓縮問題規模，還可以較早地發現指向死節點的無用分支。基于第二點原因，dom／wdeg啟發式還可以在更加全面的解空間內收集啟發式信息，從而給出更為合理的變量選擇。

5 結束語

基于Composed問題結構，提出了邊界變量的概念，并給出了在該類問題上篩選邊界變量的方法，以此為基礎設計實現了邊界啟發式方法。通過實驗分析，新啟發式求解效率要明顯高于原有啟發式方法。實驗結果也表明邊界變量在該類問題的求解過程中起著關鍵的作用。對于邊界變量，本文并沒有給出嚴格定義，直觀上邊界變量為位于問題不同求解區域相鄰邊界上的變量。Composed問題具有明顯的邊界區域，而且通過運用約束弧的松緊度特性可以快速篩選出邊界變量，因此在該類問題上進行了關于邊界變量集有效性的分析與討論。但是文中邊界變量集的篩選方法過度依賴于Composed問題結構，而不具有普遍適用性，如何在具有類似結構的眾多實際問題中篩選出邊界變量集將是接下來工作的重點。文中討論只涉及到了約束弧的松緊度，顯然網絡密度在各局部區域的變化也是問題結構的重要特性，如何將二者結合給出更為通用的邊界變量集篩選方法，是改進已有啟發式方法的重要方向。

［1］朱興軍，張永剛，李瑩，等.多值傳播的相容性技術［J］.自動化學報，2009，35（10）:1296－1301.Zhu Xing－jun，Zhang Yong－gang，Li Ying，et al.Consistency technique of multi－value propagation［J］.Acta Automatica Sinica，2009，35（10）:1296－1301.

［2］劉春暉，朱興軍，孫吉貴，等.一種改進的雙向Singleton弧相容算法［J］.吉林大學學報:工學版，2008，38（3）:666－670.Liu Chun－hui，Zhu Xing－jun，Sun Ji－gui，et al.Improved bidirectional Singleton arc consistency algorithm［J］.Journal of Jilin University（Engineering and Technology Edition），2008，38（3）:666－670.

［3］杜會盈，李占山，李宏博，等.圖分割在Singleton弧相容算法中的應用［J］.吉林大學學報:理學版，2010，48（6）:981－986.Dui Hui－ying，Li Zhan－shan，Li Hong－bo，et al.Graph partitioning applied in Singleton algorithm［J］.Journal of Jilin University（Science Edition），2010，48（6）:981－986.

［4］高健，孫吉貴，張永剛，等.參數化弧相容約束傳播［J］.吉林大學學報:信息科學版，2007，25（2）:183－187.Gao Jian，Sun Ji－gui，Zhang Yong－gang，et al.Parameterized arc consistency constraint propagation［J］.Journal of Jilin University（Information Science Edition），2007，25（2）:183－187.

［5］van Beek Peter.Backtracking search algorithms［C］∥Handbook of Constraint Programming.Francesca Rossi，Peter van Beek，Toby Walsh（eds），New York:Elsevier，2006:85－126.

［6］Li Xing－jian，Epstein Susan L.Learning clusterbased structure to solve constraint satisfaction problems［J］.Annals of Mathematics and Artificial Intelligence，2010，60:91－117.

［7］Sabin Daniel，Freuder Eugene C.Contradicting conventional wisdom in constraint satisfaction［C］∥Proceedings of CP，Rosario，Orcas Island，Washington，1994:10－20.

［8］Likitvivatanavong Chavalit，Zhang Yuan－lin，Bowen James，et al.Arc consistency during search［C］∥Veloso Manuela M （eds.）.Proceedings of IJCAI，Hyderabad，India:Morgan Kaufmann，2007:137－142.

［9］Christophe Lecoutre，Frederic Boussemart，Fred Hemery.Backjump－based techniques versus confict—directed heuristics［C］∥Proceedings of ICTAI，Boca Raton，Florida，USA:IEEE Press，2004:549－557.

［10］Haralick Robert M，Elliott Gordon L.Increasing tree search efficiency for constraint satisfaction problems［J］.Artificial Intelligence，1980，14:263－313.

［11］Grimes Diarmuid，Wallace Richard J.Learning from failures in constraint satisfaction search［C］∥Wheeler Ruml，Frank Hutter，AAAI Workshop on Learning for Search，Boston， Massachusetts，USA:AAAI Press，2006.

［12］Christophe Lecoutre，Fred Hemery.A study of residual supports in arc consistency［C］∥Veloso Manuela M（eds），Proceedings of IJCAI，Hyderabad，India，2007:125－130.

［13］Frederic Boussemart，Fred Hemery，Christophe Lecoutre，et al.Boosting systematic search by weighting constraints［C］∥R.López De Mántaras，L.Saitta，Proceedings of ECAI，Valencia，Spain:IOS Press，2004:146－150.

［14］http:／／www.cril.univ－artois.fr／～lecoutre／benchm arks.html＃