自適應的均值漂移分割算法

馬 瑜，梁慧琳，張艷寧，徐 爽

(1.西北工業大學計算機學院，陜西西安710129;2.寧夏大學研究生院，寧夏銀川750021)

1 引言

均值漂移聚類是一個基于Parzen窗的非參數核密度估計理論，為尋找局部密度的最大處。在均值漂移過程中，任何數據點都可以作為初始點進行均值漂移。將收斂到同一個點的像素點進行聚類，漂移過程中，由圖像自動決定每一類的像素數，和類的邊界［1］。

Comaniciu和Ramesh基于可變的窗寬密度估計提出一種自適應的均值漂移［2］，并且應用于圖像分割和聚類［3］。對自適應算法的提出主要是為下一步圖像處理做基礎。周芳芳、樊曉平采用自適應均值漂移聚類算法為三維數據場設計傳遞函數［4］。Lei Lin提出一種針對三維MR圖像的自適應分割方法，其主要思想也是采用自適應的帶寬設計，再加入 K-Means算法［5］。Xinhong Zhang為了圖像處理時降低計算時間和計算維度，提出自適應分割算法，其主要思想是運用了對一幅圖像的概率密度估計來計算進行帶寬設計，再加入本地特征散列法進行圖像分割 。袁勝智、謝曉方提出了一種基于Kalman-mean shift的自適應跟蹤算法，在mean shift算法中加入了一個尺度更新項，通過尺度更新對運動目標，特別是目標尺寸變化的目標進行自適應跟蹤［7］。

基于圖像處理中對圖像分割的高效、精確的要求，每一幅圖像帶寬范圍不同，而且，一幅圖像，有的部分需要精細地分割，有的部分又不需要。本文提出一種自適應的窗寬計算方法。由每個像素點與周圍點的關系以及圖像的直方圖來計算每個像素點的窗寬，從而進行自適應的分割。

2 均值漂移算法簡介

2.1 均值漂移向量

給定d維空間Rd中的S個樣本點s。在x∈X處，改進的樣本均值公式為［8］:

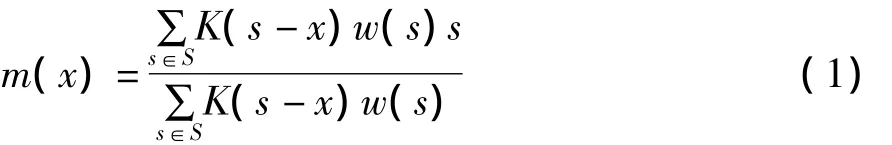
樣本均值與像素點的偏移量m(x)－x稱為均值漂移向量，記為Mh(x)。其中，K稱為核函數。核函數可以控制因距離不同，對像素點X的均值漂移向量貢獻的重要性不同。K為核函數的條件為:它存在一個剖面函數，即:

并滿足:

(1)k是非負的;

(2)k為非增，如果 ka＜b，k(a)≥k(b);

一般常用的核函數有兩種，單位均勻核函數與單位高斯核函數。

單位均勻核函數:

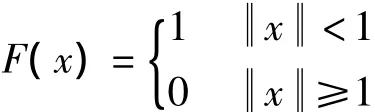
w(s)為權值，權值用來控制在核函數范圍內，不同的樣本點，重要性不同。它滿足歸一化條件:

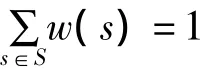
均值漂移向量表示為:

2.2 均值漂移算法

均值漂移算法是尋找局部密度最大值的過程。

均值漂移迭代算法執行過程如下:

(1)計算樣本均值m(x)。

(2)計算樣本均值與像素點之間的偏移量m(x)－x。

(3)判斷如果樣本均值與像素點之間的偏移量小于一個給定的誤差值，結束循環，樣本均值為像素點收斂的模式點;否則把m(x)賦給x，執行(1)繼續。

3 自適應窗寬

在聚類中，帶寬h決定了核函數的影響范圍，窗寬h對核密度函數估計過程以及最終的聚類結果都有很大影響。如果h取值很小，密度函數f(x)相當于n個數據對象為中心的函數的疊加，每個像素點周圍的密度函數值很小，聚類結果會產生很多類。如果h無窮小，那么每個像素的密度等于1/n，并且自成一類;如果h取值很大，f(x)稱為n個變化緩慢且寬度很大的基函數的疊加，每個像素周圍的密度函數值比較大且近似相等，相距較近的聚類將被合并。如果h無窮大，所有像素的密度等于1且被聚合為一類。所以，盡可能準確的密度估計結果和聚類結果來自于窗寬h的選擇。選擇窗寬h時應盡可能的使密度函數f(x)體現原始數據的分布特性。確定窗寬h后，通過搜索密度函數的局部極大值點實現圖像的分割［9］。

3.1 直方圖

本文使用直方圖對圖像的像素點的特征進行統計。直方圖是一種統計圖，對于一幅圖像來說，通過統計圖像中各個像素點的數量，從而對圖像的像素分布有一個直觀了解。通常，通過直方圖可以對圖像進行直方圖歸一化，直方圖拉伸，直方圖匹配。

一幅數字圖像在范圍［0，G］內共有L個灰度級，其直方圖定義為離散函數h(rk)=nk，其中rk是區間［0，G］內的第K級亮度，nk是灰度級為rk的圖像中的像素數。

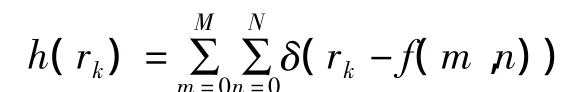
其中，δ是 Kronecher符號［10］。

3.2 圖像的直方圖獲取

對于一幅圖像來說，如果它是灰度圖像，則為單通道圖像，如果它為彩色圖像，應該包含三個通道:R(Red)，G(Green)，B(Blue)。彩色圖像和灰度圖像的直方圖獲取步驟是相同的，對于彩色圖像，計算其二維直方圖。

對于RGB圖像，由于其處理時計算量較大。先將其轉化到HSV空間(色調、飽和度、數值)。該顏色系統比RGB系統更接近于人們的經驗和對顏色的感知。彩色圖像提取其H、V顏色通道的，統計每種顏色分量的像素數占圖像總像素數的比例，從而得到圖像各種顏色分量的比例分布。

灰度圖像直接計算其灰度像素值的直方圖，并將其歸一化，進行保存。

3.3 自適應窗寬h的計算

目前帶寬的計算主要有兩類，一類是固定帶寬，一類是自適應帶寬。固定帶寬在迭代過程中，帶寬h保持不變，因此需要計算相對于全局的最優帶寬，在圖像分割過程中，效率低，分割效果不好。而且，不同的圖像，最優帶寬并不在一個范圍內，圖像分割中參數的確定是一個很大的工程。因此，圖像分割中，采用自適應帶寬，理論上會獲得比較好的分割效果。根據圖像像素點的局部特征，自適應的設計迭代帶寬，對密度大的區域采用小帶寬，對密度小的區域則采用大帶寬。

由以上的說法，令固定帶寬h=h(xi)，即每個像素點的帶寬均不一樣。一幅圖像，如果從它的直方圖來統計看，這個統計思想非常地符合在核函數中窗寬的選擇思想，即對密度大的區域采用小帶寬，對密度小的區域則采用大帶寬。像素分布于帶寬成反比關系。所以，使用二維直方圖對核函數的窗寬進行計算，是有用的。根據直方圖的定義，直方圖也可以看作一個歸一化的概率密度函數f(xi)［11］。將每個樣本點的密度估計用作選擇h(xi)的特征，取f(xi)倒數的平方根:

式中，h0是一個初始的固定帶寬，λ是常數。

為獲得一個自適應的帶寬，f(xi)，λ必須首先計算。自適應窗寬的均值漂移算法步驟為:

(1)找到一個對圖像所有像素點都滿足的估計f(xi)，在這，f(xi)為我們所取圖像的二維直方圖。

(2)窗寬因子λ的定義為:

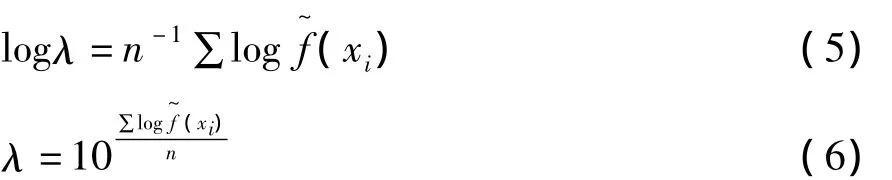
(3)對于每個像素點 xi計算其自適應的窗寬h(xi):

則自適應的均值漂移向量可表示為:

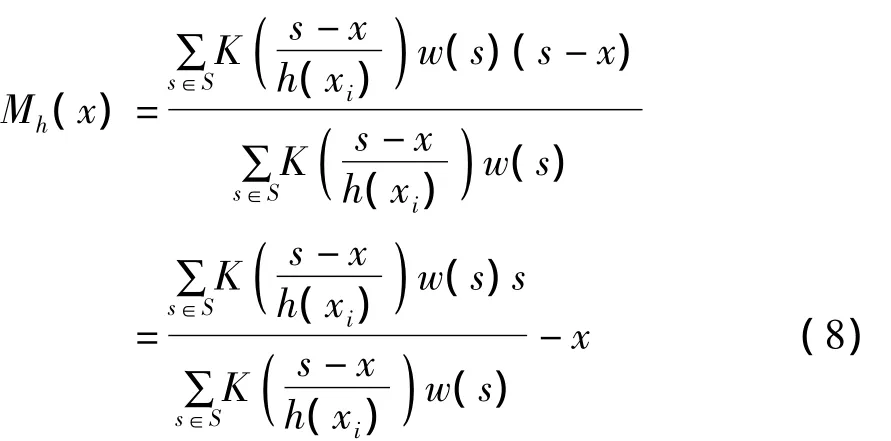
將計算后的每個點的窗寬在分割中帶入，便可得到自適應的分割結果。

4 實驗結果及分析

本實驗使用 Intel Core2，2.10 GHz，2G內存的HP筆記本，軟件使用Matlab 2008版本。與原均值漂移分割算法［7］從分割結果進行對比。hr為均值漂移算法的值域帶寬，hs值漂移算法的為空域帶寬。分割后圖像聚類區域像素點最小數量為500。算法中最大迭代次數為100，誤差系數ε=0.01。本文采用圖像大小為256×256或120×90。

圖1 灰度圖像的分割

取一幅灰度圖像，如圖1(a)所示圖1(a)的灰度圖像相對較為復雜。圖1(b)為使用本文自適應算法進行圖像分割的結果。圖1(d)、(e)、(f)分別為使用固定帶寬的均值漂移算法分割后的結果。對于固定帶寬參數的選擇，值域帶寬選定16。進行頻域帶寬的單變量參數變化。由圖可以看出，在圖1(f)中帶寬選擇小了，分割結果太過精細，無法很好的將背景和前景分開，這就是過分割問題，對于一些不存在的細節也會分割。圖1(d)和圖1(e)進行對比，圖1(e)能相對較好地將人的輪廓分割出來，但是，圖像分割得結果不完整。而自適應的均值漂移算法，不僅很好地將人完整地分割，而且，在相機的腳架以及相機部分，都很清晰地分割出來。我們從圖1(b)中可以看到一幅很完整的圖像，包括圖像的前景、背景以及一些細節。

圖2(a)為一幅復雜的彩色圖像。圖2(b)為使用本文自適應算法進行圖像分割的結果。圖2(d)、(e)、(f)分別為使用固定帶寬的均值漂移算法分割后的結果。對于固定帶寬參數的選擇，值域帶寬選定16。進行頻域帶寬的單變量參數變化。圖2(d)中，樹葉部分好多細節沒有分割出，前景和背景很模糊。圖2(f)較好的分割出了樹葉的部分，但是相比圖2(e)，在藍天部分，地面部分又存在過分割的問題。圖2(b)圖使用自適應的分割算法。不僅很好地分割出樹葉，而且對于地面和藍天，分割精度又不至于太細導致過分割。

圖2 彩色圖像的分割

5 結論

本文根據在圖像處理中對圖像分割前期準備工作高效、準確的要求，結合圖像的直方圖，提出一種自適應的均值漂移分割算法。算法首先利用圖像的直方圖估計出圖像的概率密度。對每個像素點根據其周圍特征以及概率分布計算它的帶寬值。使得在均值漂移濾波時可以達到自適應的效果。如果沒有自適應帶寬，那么在確定參數時需要大量的實驗。實驗結果表明，改進算法很好的解決了固定帶寬均值漂移算法在確定帶寬時效率低，分割效果差的問題。自適應的均值漂移分割算法可以有很好的分割結果。

［1］ Zhang Xinhong，Cui Yanbin．An adaptive mean shift clustering algorithm based on locality-sensitive hashing［J］．Optik，2012，123(20):1891 －1894．

［2］ D Comaniciu，V M P Ramesh．The variable bandwidths mean shift and data-driven scale selection［J］．IEEE Int．Conf．Comput．Vis，2001，(1):438 －445．

［3］ H B Helbig，M O Ernst．Optimal integration of shape information from vision and touch［J］．Exp．Brain Res．2007，4(179):595 －606．

［4］ Zhou Fangfang，Fan Xiaoping．Designing transfer function based on adaptive bandwidth mean shift clustering algorithm［J］．Information and Control，2007，36(5):585 －591．(in Chinese)周芳芳，樊曉平．基于自適應帶寬均值漂移聚類算法設計傳遞函數［J］．信息與控制，2007，36(5):585－591．

［5］ Lei Lin．Adaptive pixon represented segmentation(APRS)for 3D MR brain images based on mean shift and Markov random fields［J］．Pattern Recognition Letters．2011:1036－1043

［6］ Zhang Xinhong．An adaptive mean shift clustering algorithm based on locality-sensitive hashing［J］．Optik．2012:1891－1894．

［7］ Yuan Shengzhi，Xie Xiaofang．Bandwidth-adaptive tracking algorithm based on Kalman-mean shift method［J］．Laser＆ Infraded，2009，39(5):558 －561．(in Chinese)袁勝智，謝曉方．一種基于Kalman-mean shift的自適應跟蹤算法［J］．激光與紅外，2009，39(5):558 －561．

［8］ Y Cheng，Mean shift，mode seeking，and clustering［J］．IEEE Trans．Pattern Anal．Machine Intell，1995，17:790－799．

［9］ Gan Wenyan，Li Deyi．Hierarchical clustering based on kernel density estimation［J］．Journal of System Simulation，2004，16(2):302 －307．(in Chinese)淦文燕，李德毅．基于核密度估計的層次聚類算法［J］．系統仿真學報，2004，16(2):302 －307．

［10］ Hong MingJian．Study on the Adaptive Histogram Modification ForImage Enhancement［D］．Chongqing:Chongqing University，2002，4．(in Chinese)洪明堅．圖像增強的自適應直方圖修正算法研究及其應用［D］．重慶:重慶大學，2002，4．