對兩個重要極限的新認識

王夢潔

（武漢理工大學，湖北 武漢430070）

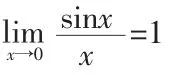
1 兩個重要極限的新證明

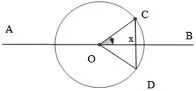
證法1 利用幾何圖形，作一單位圓（如圖所示）：

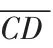
證法2 利用拉格朗日中值定理，選取函數f（x）=sinx，則f（x）在［0，x］上滿足拉格朗日中值定理的條件，且f′（x）=cosx，因而在（0，x）內至少存在一點ξ 使得

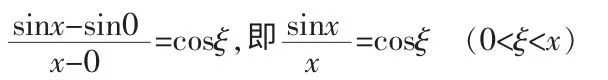
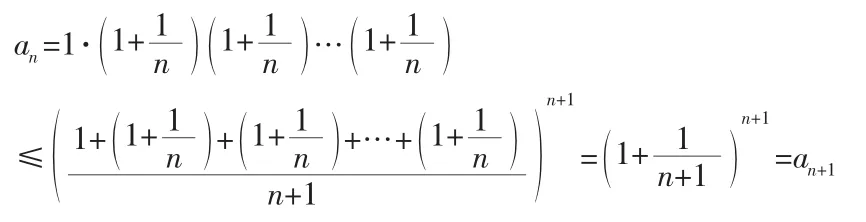
故｛an｝單調遞增，又因，故an≤4，即｛an｝有上界。

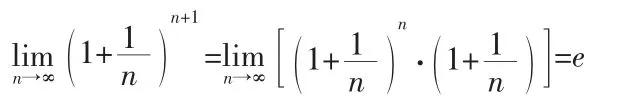
令x＝－（t＋1），則x→－∞時，t→＋∞，從而

1.3 兩個重要極限的特征及其推廣

2）上下一致：即sin 函數內的式子要與分母的式子一致

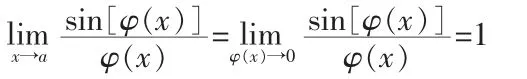
1） 1∞型

2）“無窮小”與“無窮大”的解析式為倒數

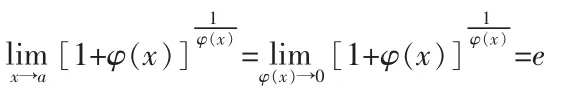
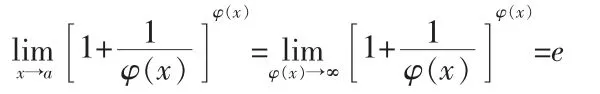
2 兩個重要極限的應用

2.1 兩個重要極限在計算一元函數極限中的應用

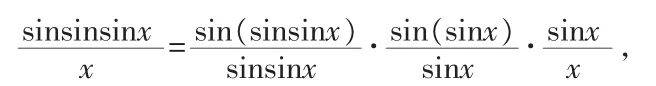
當x→0 時，sinsinx→0，由第一個重要極限及其一般形式立刻得到：

2.2 兩個重要極限在二元函數極限中的應用

二元極限與一元函數極限概念的本質是一致的，都是對函數在其自變量的某個變化過程中函數值的趨向性的反映。由于二元函數的自變量有兩個， 其變化過程比一元函數自變量的變化過程復雜的多，同時對二元函數極限的運算有時更是無從入手。 實際上，在二元函數的求解中，因為二元函數極限的定義與一元函數的定義有著完全形同的形式， 這使得一些一元函數的極限運算都可以平行推廣到函數上來，特別是兩個重要極限在二元函數極限運算中的應用。

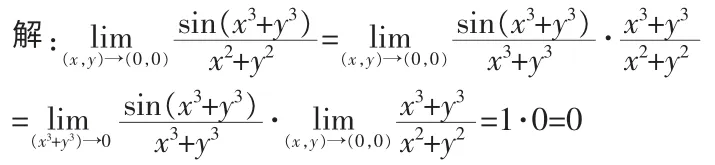
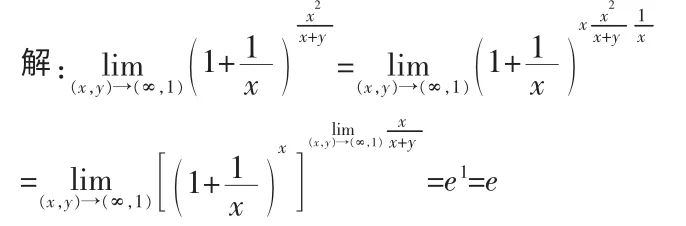
對于二元函數極限的運算除了利用重要極限外， 還有很多的方法，比如利用不等式，使用夾逼準則等，這里主要是討論了重要極限在二元函數的應用，加深了對重要極限在二元函數極限運算中作用的理解，以更好的解決二元函數問題。

總之，對重要極限進行應用，推敲，變化等，不僅是對本身的深入，也是對極限概念性質的深入。

［1］華東師范大學數學系.數學分析[M].高等教育出版社，2007.

［2］代瑞香，劉超高.一重要極限的另證[J].高等函授學報，2010 年6 月第23 卷第3 期：33-33.

［3］孫幸榮.一個重要極限的新證及其推廣[J].佳木斯教育學院學報.2010 年第1期：107-107.

［4］張霞.兩個重要極限在二元函數極限中的應用[J].上海電力學院數理系:45-46.