32APSK調制在多徑信道中的星座優化

郭淑霞 ， 李 濤 ，2， 董中要 ， 劉孟江

（1.西北工業大學 無人機特種技術重點實驗室，陜西 西安 710065；2.93975部隊 新疆 烏魯木齊 830005）

隨著數字寬帶業務的增大和系統容量的擴展，頻譜帶寬資源越來越緊張，使用代價越來越大，為了提高頻帶效益，信號的傳輸大都考慮采用幅度與相位相結合的高階調制方式[1]。而傳統的矩形MQAM，存在較多的幅度，通過非線性轉發器時，一部分點離飽和點偏遠，功率效益不高，而那些接近飽和狀態工作的信號點非線性失真影響嚴重[2]，加大了預失真校正的復雜度。因此，在設計信道、頻譜利用率高的調制星座時，采用的高階方案應盡量減少信號幅度的起伏，這樣星座形狀應呈圓形、圓周個數少的環形MAPSK成為首選。

星座的優化設計方法就是根據信道衰落特性，測算星座點幅度和相位的變化，在調制端對星座進行非對稱的設計，使其經過衰落信道后，能夠使相位和幅度恢復原來的標準映射星座，而在解調端解調時，仍然以標準的映射星座進行解調，提高信號抵抗信道衰落的能力。

傳統的星座MASPK優化方法有最小歐氏距離最大化原則和互信息最大化原則[3-4]。這兩種方法在高斯信道中性能良好，但是在多徑衰落信道下因不能有效的對相位失真進行矯正，使性能大大降低。本文采用調制星座的星座點旋轉來抵抗多徑失真，在不增加硬件負擔的前提下，可以較好的克服多徑信道衰落對信號的影響。

1 多徑Rice模型下的成對差錯概率分析

圖1給出了MAPSK的調制系統圖。系統目的是通過對MAPSK映射星座的設計，選取最優的相對半徑和相對相位，在調制端對星座進行預失真矯正，以抵消信道衰落對信號的影響。系統中調制信號被分解為同向分量和正交分量，兩路信號受到高斯白噪聲和多徑信道衰落的影響。這里的多徑衰落我們采用Rice模型[5]進行分析。

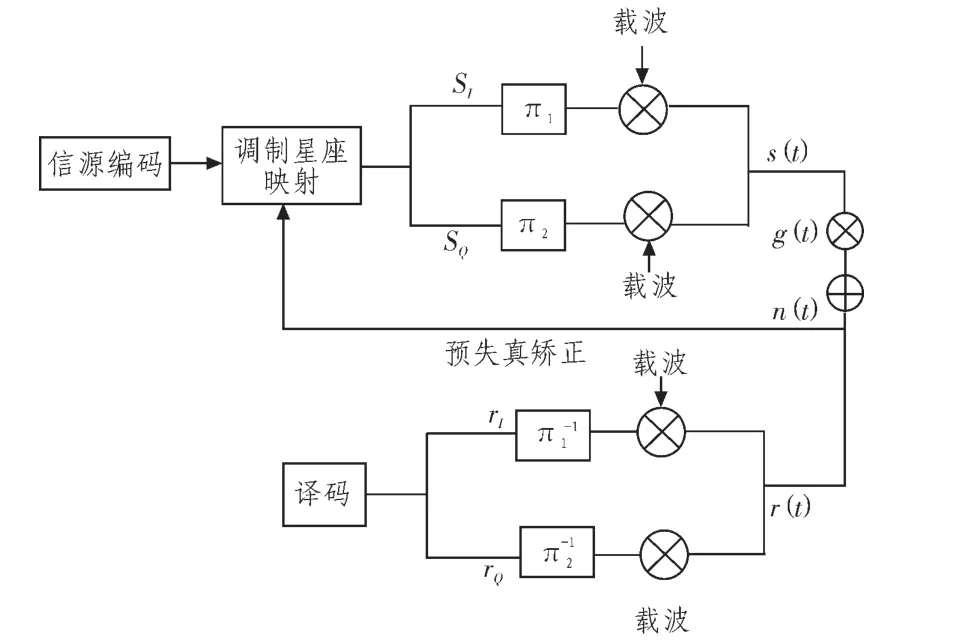
圖1 MAPSK調制系統圖Fig.1 System diagram of the MAPSK modulation

接收信號可以表示為：

其中 g（t）表示衰落分布隨機變量，n（t）表示高斯白噪聲。將接收端信息序列分為同向分量和正交分量表示：

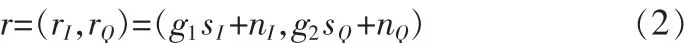
其中，g1和g2分別表示衰落信道對同向分量和正交分量的影響。 滿足 E（g1）=E（g2）=1。

其誤碼率計算公式可表示為：

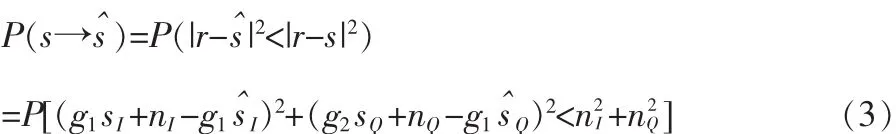
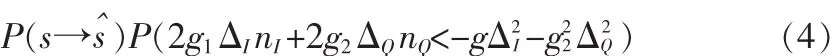
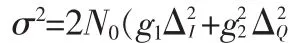
因此，在（g1，g2）條件下的成對錯誤概率為：

則，成對差錯概率可表示為：

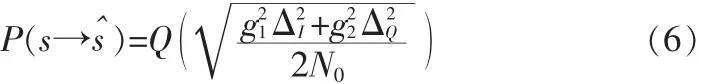
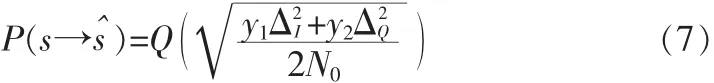
在Rice信道下，y的概率密度分布為：

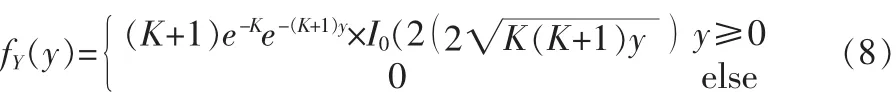
其中K表示萊斯因子，I0（）表示第一類0階修正Bessel函數。從而，賴斯信道下的誤碼率計算公式為：

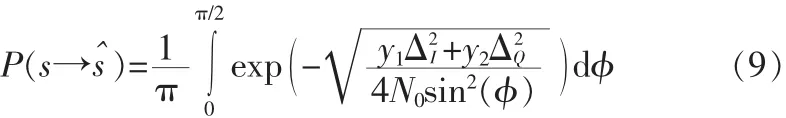
根據y的概率密度分布，可以對誤碼率進一步展開：

拉普拉斯轉換得：

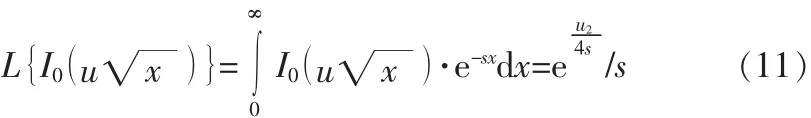
從而，把對y的積分轉換為：

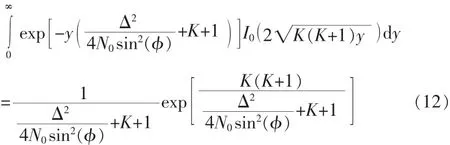
將拉普拉斯轉換代入誤碼率計算公式，可以得到：

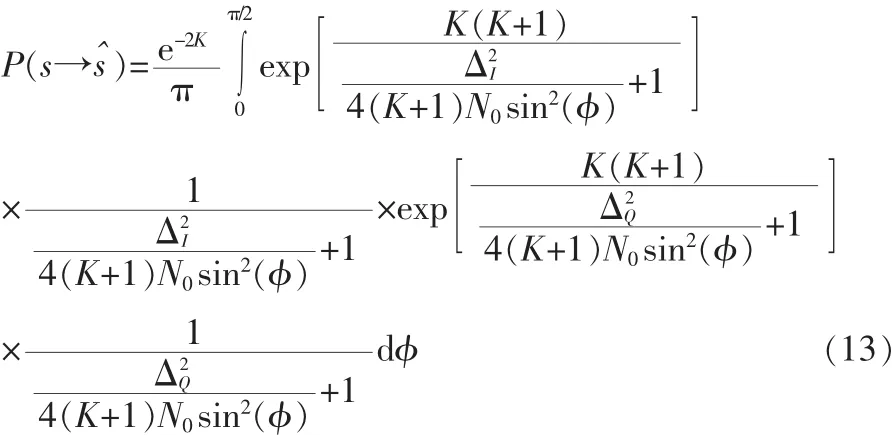
由此可以得到：

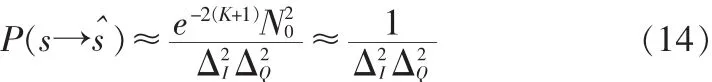
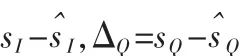
2 32APSK調制星座點成對差錯概率計算

1）首先按照最小歐氏距離最大化原則對32MAPSK星座進行優化，得到歐氏距離最大化的星座分布[6]為：4-11-17APSK結構，內圓和中間圓的半徑比為2.176，中間圓與外圓的半徑比為1.540，最大的歐氏距離為：0.419 9。經過最小歐氏距離最大化之后的星座圖如圖2所示。

圖2 最小歐氏距離最大化之后的32APSK星座圖Fig.2 Constellation diagram of the 32APSK witch the minimum Euclidean distance is maximized

2）假設每個環上的最優的旋轉相位分別為：θ1表示第一環上的最優旋轉相位、θ2表示第二環上的最優旋轉相位、θ3表示最外環的最優旋轉相位。 根據（14）式，結合星圖點距的三角函數關系，得出包含θ1，θ2和θ3三變量的各點成對差錯概率公式 p（s1→sj）i=1，…，M；j=1，…，M&j≠i如下（在此處假設信號傳輸的能量為1）。

對于1點：

直至計算出點32的成對差錯概率

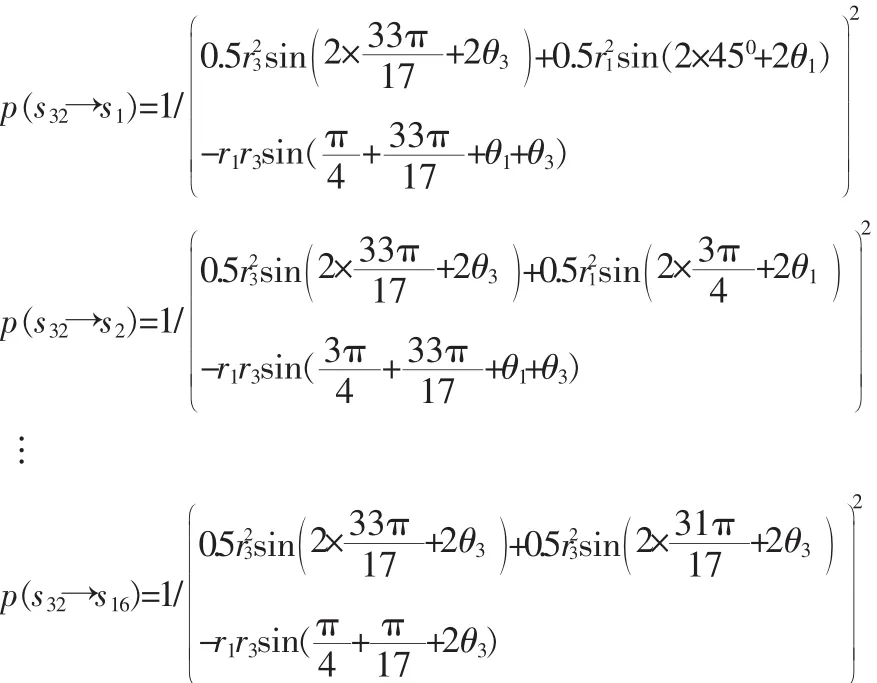
3 計算機仿真搜索

對以上所有成對錯誤概率構建求和函數，以此進行計算機仿真搜索得到3個圓環的相位旋轉角度值。因為構建的求和函數有 2個變量 θ1，θ2和 θ3，再求其中一個變量時，我們假定其他變量為一固定值。下圖為仿真搜索的結果。

我們設定圖3單位刻度為0.1 rad；圖4單位刻度為0.05 rad；圖5單位刻度為0.05 rad。根據上面的仿真圖可以看出，最優的θ1旋轉角度為0.2 rad，即旋轉角度為11.459 2度，最優的θ2旋轉角度為0.15 rad，即旋轉的最佳角度為8.594 4度，最優的θ2旋轉角度為0.1 rad，即旋轉的最佳角度為5.729 6度。圖6為優化前后的32APSK的星座圖

4 仿真驗證

在Rice模型中，對使用傳統最小歐氏距離最大化原則和本文所提的星座旋轉方法的4-7-11APSK優化結果進行MATLAB誤碼率性能仿真。

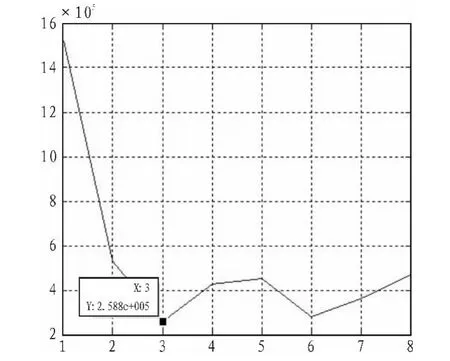
圖3 θ1的旋轉角度與成對差錯概率的關系Fig.3 The relationship between the rotation angle θ1and the pairwise error probability

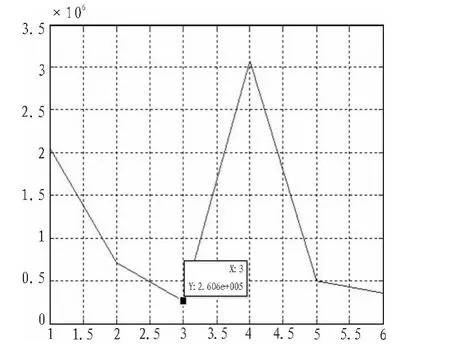
圖4 θ2的旋轉角度與成對差錯概率的關系Fig.4 The relationship between the rotation angle θ2and the pairwise error probability

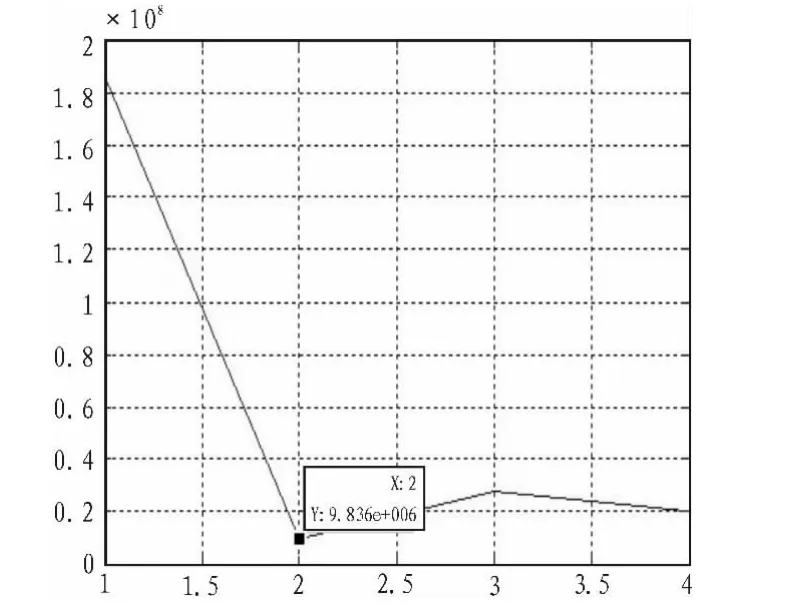
圖5 θ3的旋轉角度與成對差錯概率的關系Fig.5 The relationship between the rotation angle and the pairwise error probability

仿真條件：設定內圓和中間圓的半徑比為2.176，中間圓與外圓的半徑比為1.540。采用相位旋轉時設定最優θ1旋轉角度 11.459 2度，最優 θ2角度8.594 4度，最優 θ2旋轉角度5.729 6度。

5 結 論

仿真結果表明：由于最小歐式距離最大化原則，只對半徑比進行優化，星座圖的圓環相位沒有根據信道特性做矯正，所以效果欠佳。而本文給出的星座旋轉能依據信道特征，較好的克服信道衰落對星座的扭曲，圓環半徑和相位均得到了矯正，具有良好的性能優勢。

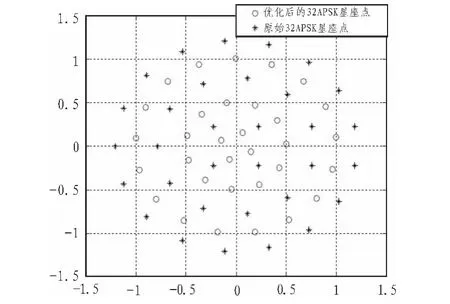
圖6 優化前后的32APSK星座圖Fig.6 The constellation diagram of 32APSK before and after optimization

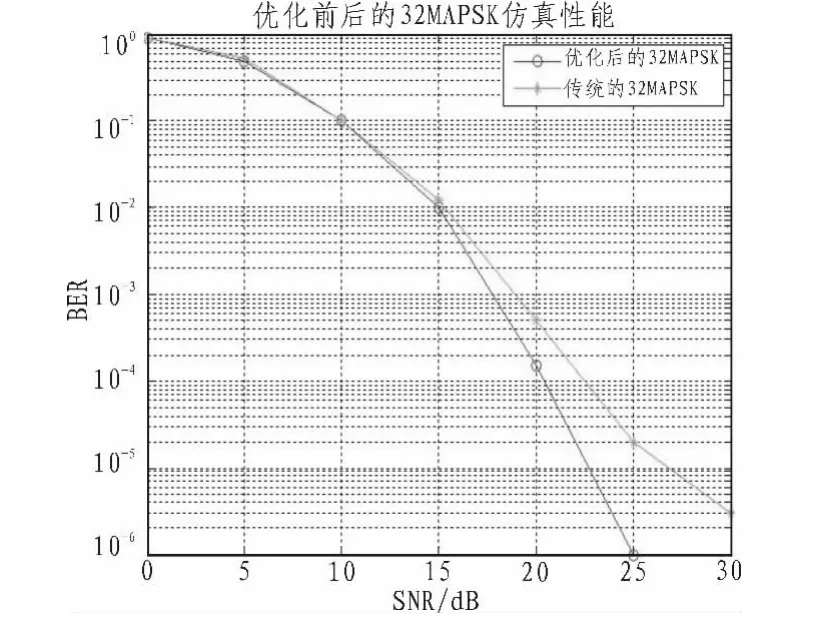
圖7 優化前后32APSK調制的性能Fig.7 The performance of 32APSK modulation before and after optimize

[1]達新宇.通信原理教程 [M].北京:北京郵電大學出版社，2005.

[2]Luca Giugno，Marco Luise，Vincenzo Lottici.Adaptive Pre2and Post2compensation of Nonlinear Distortions for High2level Data Modulations[J].IEEE Trans Commun，2004，3 （5）:1490-1495.

[3]De Gaudenzi R.，Guillén i Fàbregas A，Martinez A.Turbocoded APSK modulations design for satellite broadband communications[J]. International Journal of Satellite Communications and Networking，2006，24：261-281.

[4]De Gaudenzi R，Guillén i，Fàbregas A，et al.Performance analysis of turbo-coded APSK modulations over nonlinear satellite channels[J]. IEEE Transactions on Wireless Communications，2006，5（9）：2396-2407.

[5]Xiao Chengshan，Zheng Yahong R，Beaulieu C.Statistieal simulation models for rayleigh and rice fading channels[J].IEEE International Conference on Communications，2003（5）:3524-352.

[6]黃國棟.高階非對稱性星座調制網格編碼調制研究[D].西安:西北工業大學，2011.