潛用平臺慣導陀螺漂移估計的新方法

夏衛星，楊曉東，王 煒

(1.海軍潛艇學院訓練大隊，山東 青島 266042;2.海軍潛艇學院航海觀通系，山東 青島 266042)

0 引言

潛用平臺慣導系統能自主提供潛艇的位置、速度、姿態等信息，不僅是潛艇安全航行的保障，也是艇載武器系統的基準信息源。由于陀螺漂移等慣性器件誤差的存在，使得導航誤差隨時間不斷積累。為滿足導航精度要求，必須對陀螺漂移進行估計并補償。目前常用的陀螺漂移估計方法為基于組合導航的 Kalman濾波［1-3］。文獻 ［4-5］將多普勒測速系統引入組合導航，并應用Kalman濾波技術估計慣性器件誤差，有效提高了導航精度。文獻 ［6］提出基于INS/GPS/CNS的位置、姿態組合模型，采用聯邦濾波器改善系統導航精度。文獻 ［7-11］利用Kalman濾波，對天文/慣性組合系統的融合方案進行了仿真。文獻 ［12］提出將UKF用于INS/無源北斗組合導航系統，使INS/無源北斗組合導航系統的導航精度得到大幅提高。上述文獻分析表明，只有長時間實時、連續獲得外界測量信息，Kalman濾波器才可有效估計慣性器件誤差，如陀螺漂移等。此方案在水面艦艇等易于獲取外界信息的載體上較容易實現。然而，對潛艇而言，長時間連續獲得外界信息這一要求無法保證其隱蔽性，因此基于組合導航的Kalman濾波方法在潛用平臺慣導方面適用性不強。為保證潛艇隱蔽性，滿足高精度導航要求，設計了一種針對潛用平臺慣導的陀螺漂移估計新方法。該方法打破組合導航時長時間連續獲得外界信息這一要求，基于舒拉振蕩周期，利用間斷獲得的外界速度、位置信息，建立平臺慣導系統速度、位置誤差模型，采用參數辨識法對前一舒拉周期進行恢復，最后采用Kalman濾波技術估計陀螺漂移以及平臺水平誤差角，不僅在一定程度上保證了潛艇的隱蔽性，同時也提高了導航精度。

1 常值陀螺漂移對慣導系統的誤差影響

文獻［13］基于Laplace變換給出了常值陀螺漂移εx，εy，εz對平臺慣導系統各誤差量的影響。其中，εx對系統速度、位置誤差的影響為:

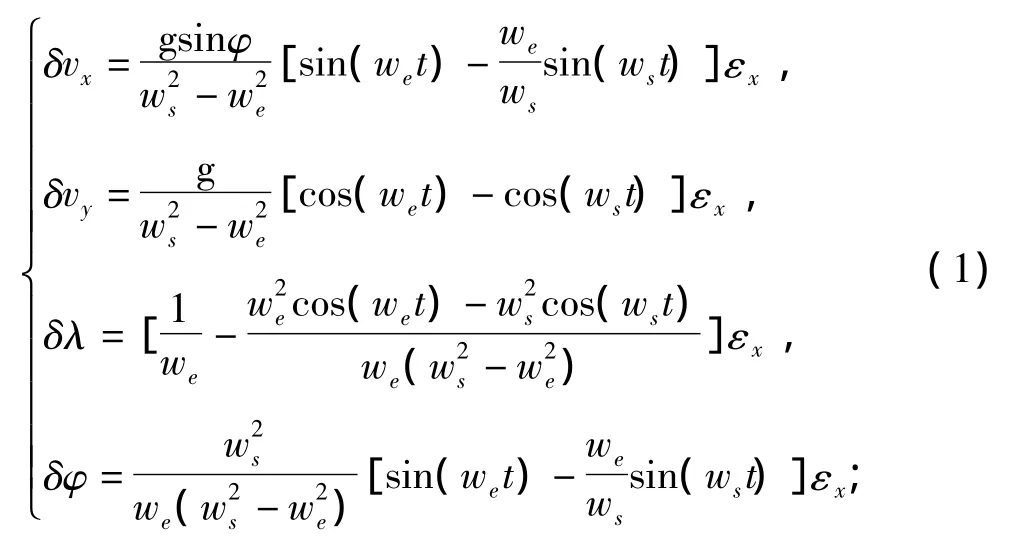
εy對系統速度、位置誤差的影響為:

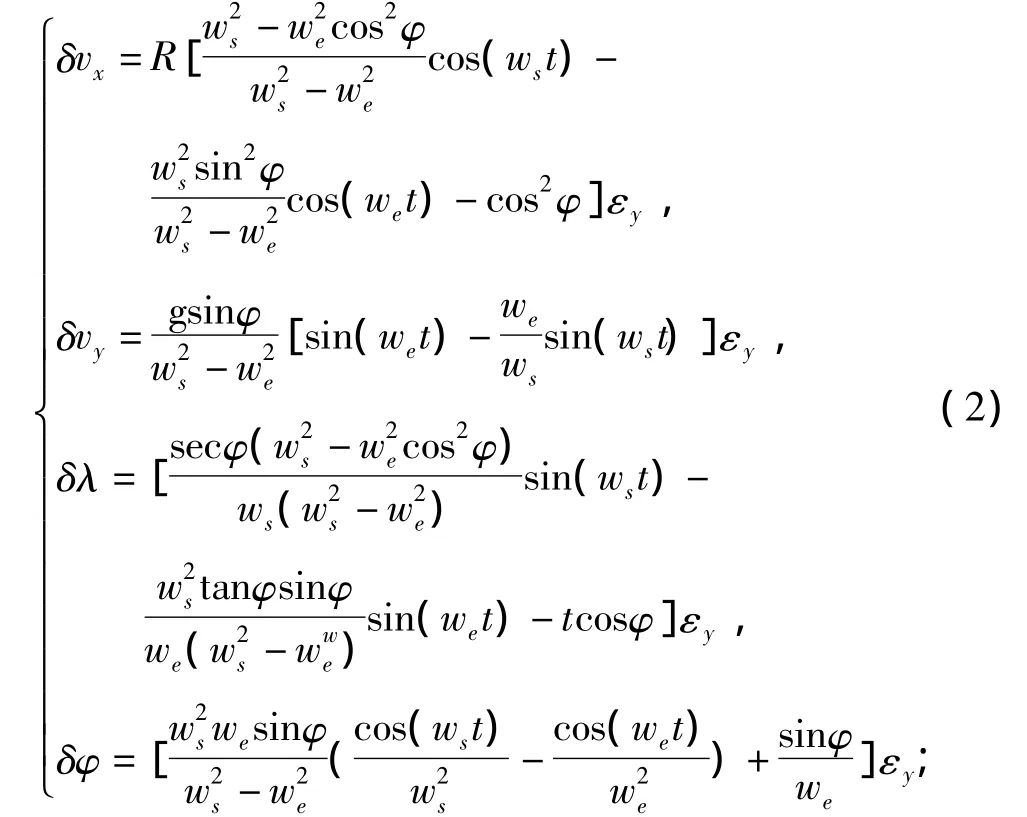
εz對系統速度、位置誤差的影響為:

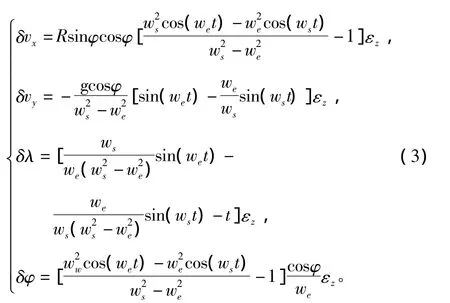
式中:δvx，δvy，δλ，δφ 分別為平臺慣導系統東、北向速度誤差及經、緯度誤差;R為地球半徑;g為重力加速度;we為地球自轉角速度;ws為舒拉角頻率;φ為地理緯度;t為時間。

由式(1)～式(3)可知，陀螺常值漂移造成速度、位置的常值誤差、隨時間增長的誤差以及周期振蕩性誤差，其中振蕩頻率包括we和ws。

2 基于舒拉周期的慣導系統短時誤差模型及不確定度評估

2.1 慣導系統短時誤差模型建立

由上述誤差分析結果可知，無阻尼慣導系統長時間導航時，速度、位置誤差會受到舒拉周期及地球周期的調制，且伴隨常值誤差和隨時間增長的誤差，故短時間內可將慣導系統模型簡化為:

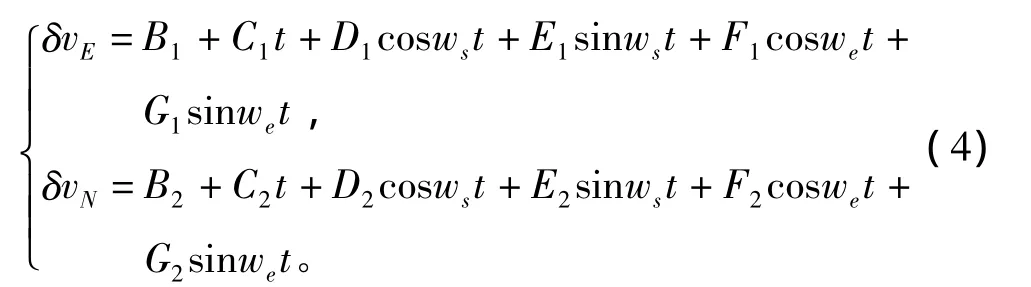
式中:δvE和δvN分別為東向、北向速度誤差，δvE= δvx，δvN= δvy;B1，C1，D1，E1，F1和 G1分別為東向速度誤差系數;B2，C2，D2，E2，F2和 G2分別為北向速度誤差系數。

由于ws＜＜we，故對式(4)最后2項作線性化泰勒展開，與前2項合并，且如果在1個舒拉周期之內連續幾次獲得有效的外部測量，則式(4)可簡化為:

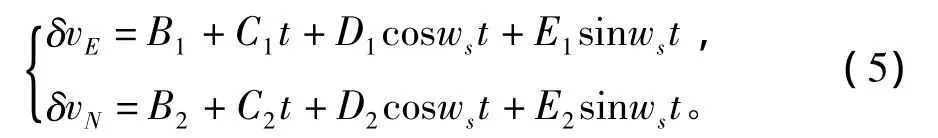
根據式(5)，位置誤差可表示為:

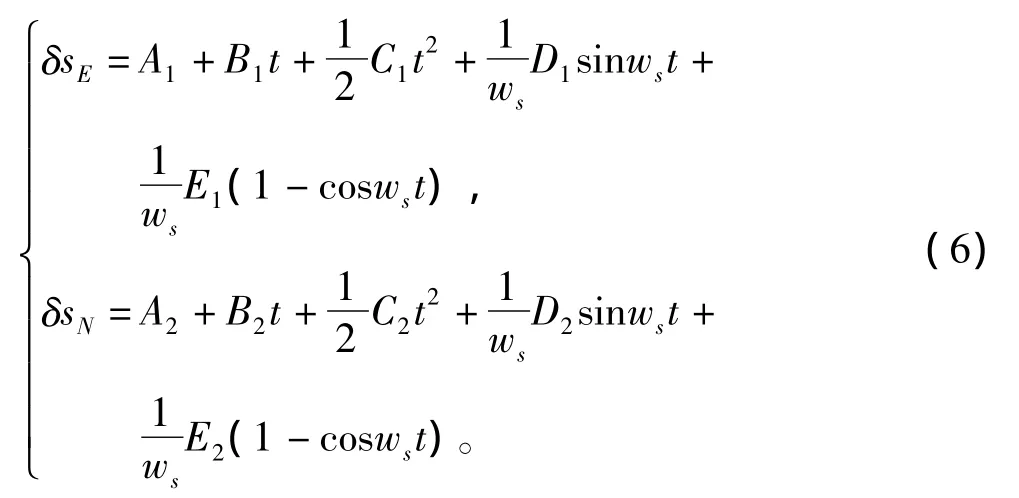
式中:δsE和δsN分別為東、北向位置誤差，δsE=δλ×Rcosφ，δsN=δφ×R;A1和A2分別為位置誤差系數。

2.2 模型參數辨識

為辨識模型參數，必須獲得3次以上有效外部測量，若時間間隔太短，則會造成較大的擬合誤差，若間隔時間太長，則無法有效辨識出模型舒拉振蕩參數，故考慮外信息采集時間間隔T=舒拉周期，共5個采樣點，時間分別為t1，t2，…，t5。

基于最小二乘參數辨識，得短時慣導誤差模型系數為:

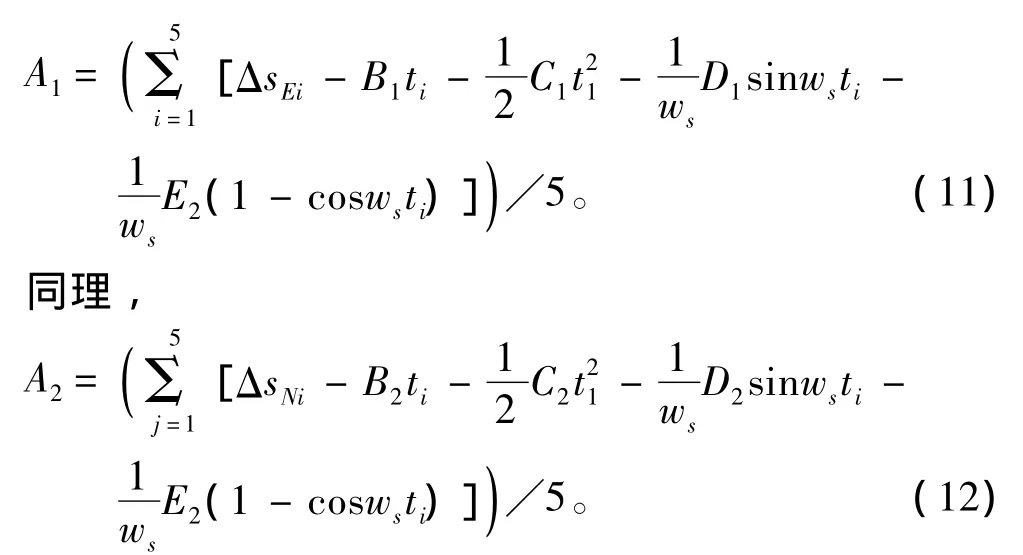
式(9)～式(12)對模型參數進行了有效辨識，即可采用模型參數恢復前一舒拉周期速度、位置誤差，時間間隔可自定。

2.3 模型不確定度評估

令 εδvx，εδvy，εδφ和 εδλ為速度誤差及位置誤差殘差;Zδvx，Zδvy，Zδφ和 Zδλ為實際速度誤差及位置誤差，均為n維向量，且

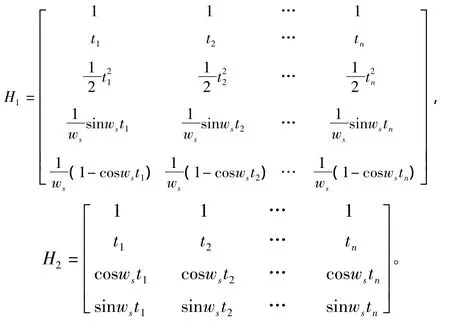
其中，n與自定時間間隔相關。

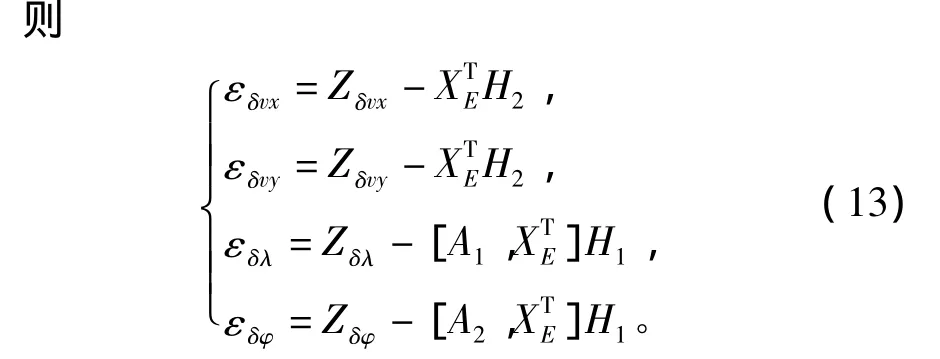
相應的模型不確定度表示為:

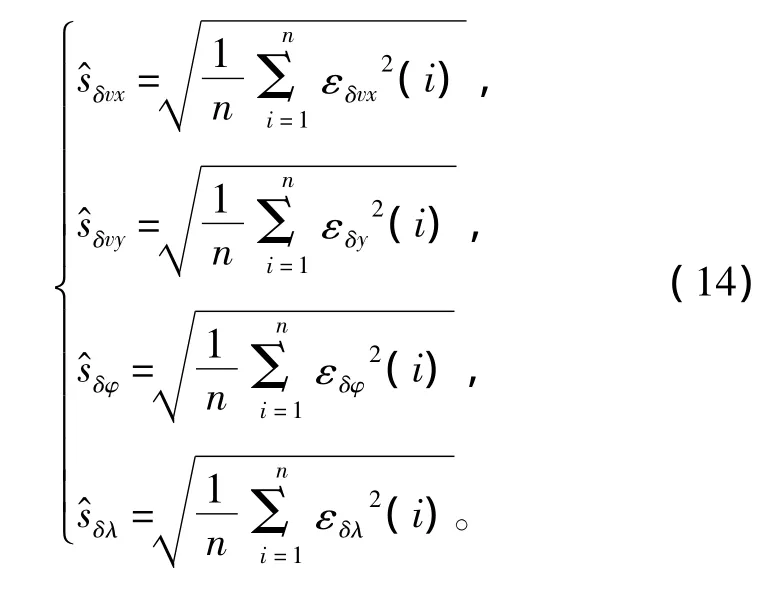
綜上，通過間斷獲得的外測數據，即每隔21.1 min采集1次，可以對模型參數進行有效辨識，恢復1個舒拉周期的速度、位置誤差，恢復間隔可自定，最后采用Kalman濾波估計陀螺漂移與平臺漂移角，改善系統精度。

3 仿真實驗

3.1 仿真條件

設定速度、位置誤差恢復間隔t=1 s。

潛艇運動參數設定:航行速度v=10 kn，初始航向 H=90°，初始位置 φ =30°N，λ =120°E。

慣導系統參數設定:平臺初始誤差α=3'，β=3'，γ=5';加速度計常值偏置ΔAX=ΔAY=10-5g;陀螺常值漂移 εX=0.01°/h，εY=0.01°/h，εZ=0.01°/h;陀螺隨機漂移相關時間為1 h，其等效漂移量級為0.01°/h。

外部測量數據設定:外測速度誤差δvx=δvy=0.1 m/s，δsE= δsN=15 m。

慣導系統工作狀態設定:首先慣導系統工作于水平阻尼狀態;進行陀螺漂移估計時，轉換至無阻尼，并連續運行1個舒拉周期，期間伴隨潛艇機動上浮、下潛;數據采集結束，工作狀態轉換為水平阻尼。

3.2 平臺慣導短時誤差模型及其不確定度

由圖(1)～圖(8)恢復曲線及不確定度檢驗結果可知，采用間斷獲取外測信息的方法可有效地辨識模型參數，建立的短時慣導系統速度、位置誤差模型可靠，位置誤差不確定度均在10 m之內，速度誤差不確定度小于0.1 m/s。

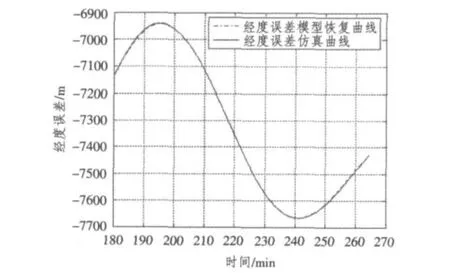
圖1 經度誤差恢復曲線Fig.1 Comeback of longitude error

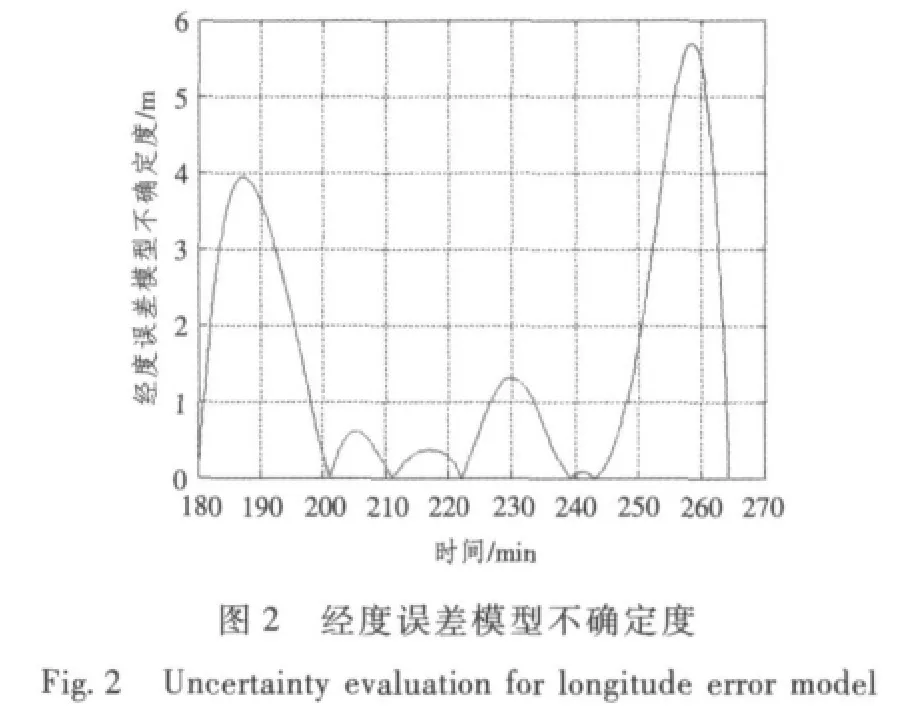
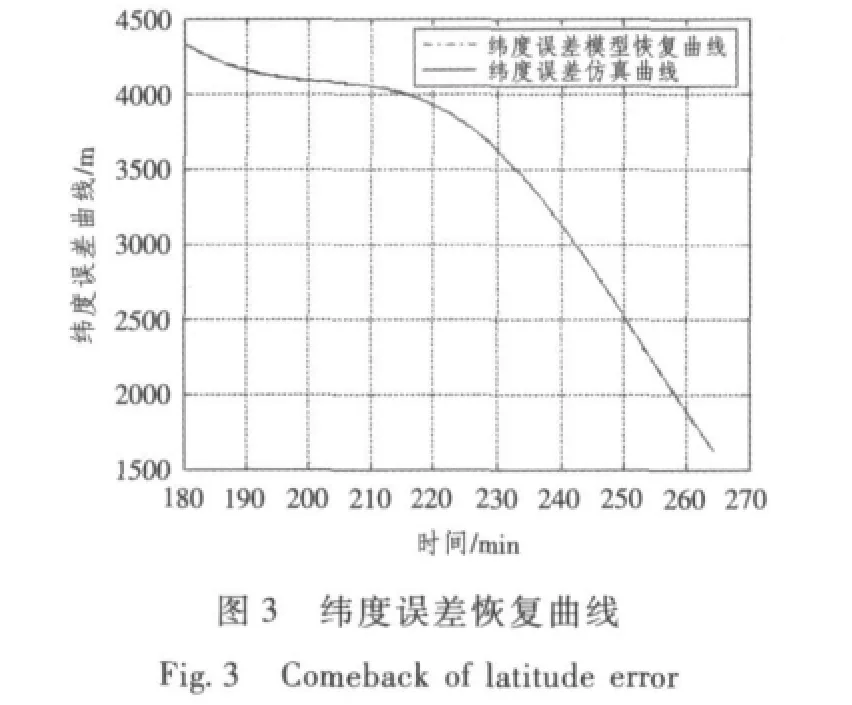
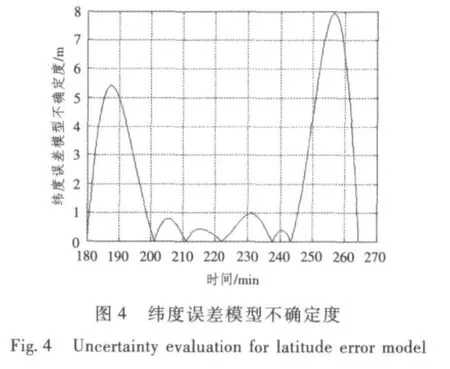
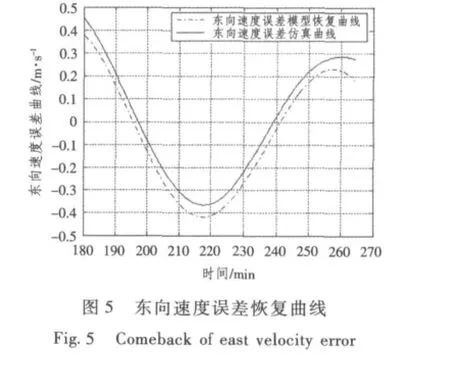
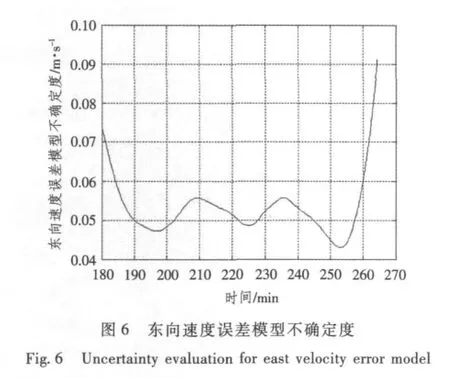
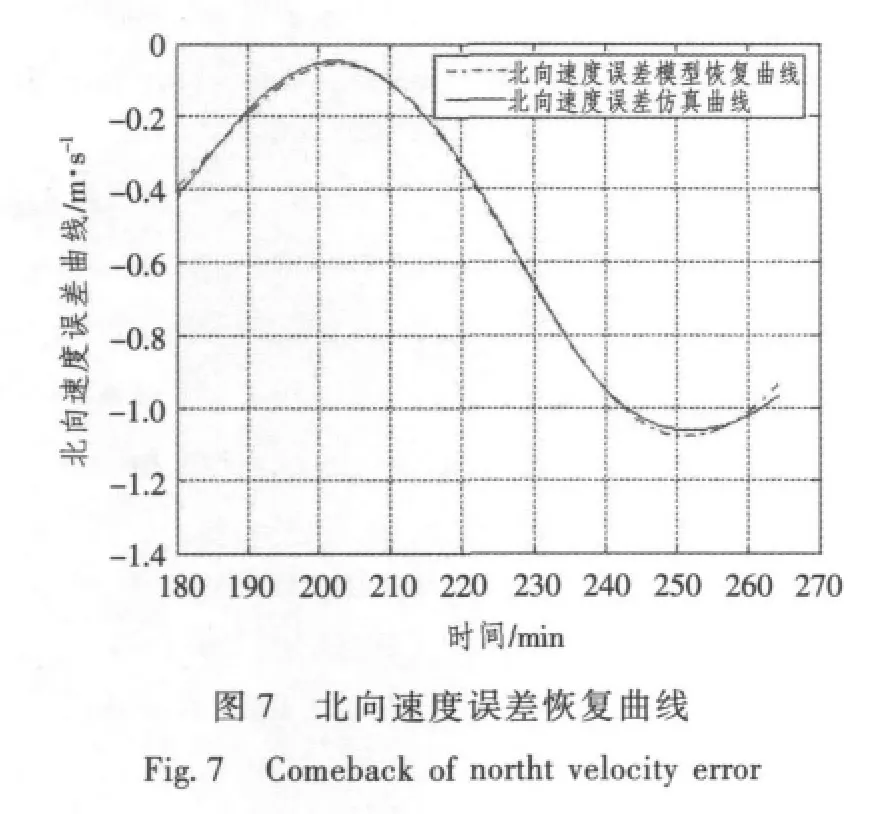
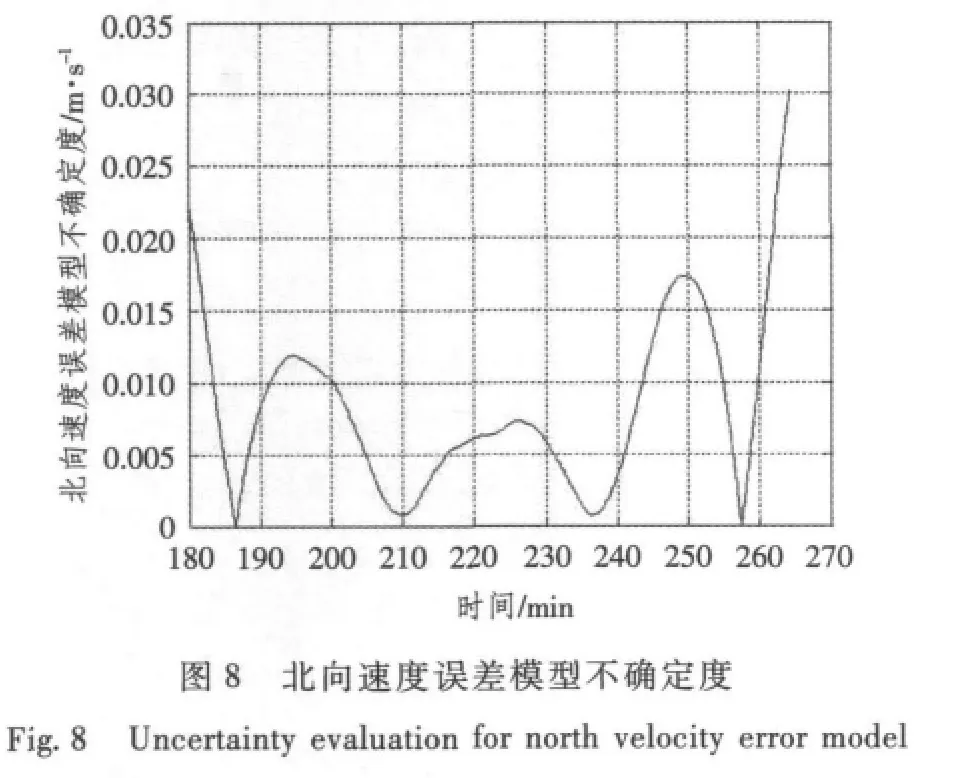
3.3 基于Kalman濾波的陀螺漂移估計

由上述驗證結果可知，恢復的誤差模型可靠，故可采用速度+位置組合方式，基于Kalman濾波估計陀螺漂移。慣導系統狀態估計結果如圖9和圖10所示。

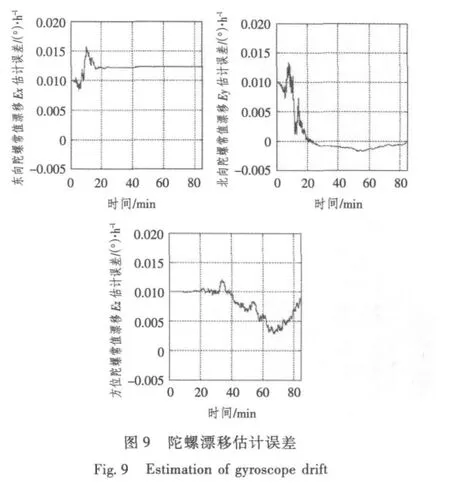
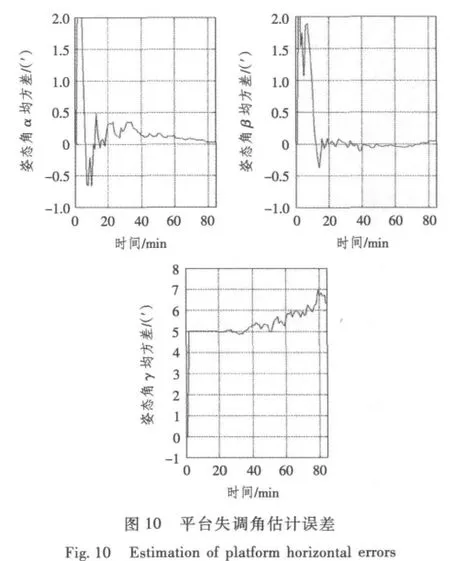
圖9和圖10估計結果表明，Kalman濾波可在1個舒拉周期內準確地估計出北向陀螺漂移及水平誤差失調角。盡管該估計結果不能滿足實時性要求，但卻能補償北向陀螺常值漂移與水平誤差失調角對慣導系統造成的影響，有效提高系統導航精度。

4 結語

針對潛艇無法長時間、連續、實時地獲得外測信息這一約束條件，采用間斷 (21.1 min)獲得的外測信息建立了慣導系統短時速度、位置誤差模型，并進行了模型的不確定度評估，最后基于Kalman濾波有效估計了陀螺常值漂移及平臺失調角。盡管建立的速度、位置誤差模型屬于前一舒拉周期，無法滿足實時性要求，但該方法卻可較為精確地估計出北向陀螺漂移和平臺水平失調角，有效抑制后續導航誤差，提高導航精度。

［1］CARLSON N A.Federated filter for fault-tolerant integrated navigation systems［C］.IEEE Position Location and Navigation Symposium，1988.110-119.

［2］HARTMAN R，HAWKINSON W，SWEENEY K.Tactical underwater navigation system position［C］//IEEE Location and Navigation Symposium，2008.898-911.

［3］DUAN S，KANG F，FU Y F，et al.An improved federated filtering method for integrated navigation system of autonomous underwater vehicle［C］//2008 Asia Simulation Conference-7th Intl.Conf.on Sys.Simulation and Scientific Computing，IEEE 2008.748-751.

［4］李佩娟，徐曉蘇，張濤.信息融合技術在水下組合導航系統中的應用［J］.中國慣性技術學報，2009，17(3):344-349.LI Pei-juan，XU Xiao-su，ZHANG Tao.Application of information fusion to integrated navigation system of underwater vehicle［J］.JournalofChinese Inertial Technology，2009，17(3):344-349.

［5］楊常松，徐曉蘇，汪麗云，等.信息融合技術在INS/GPS/DVL組合導航中的應用研究［J］.中國慣性技術學報，2006，14(5):39-43.YANG Chang-song，XU Xiao-su，WANG Li-yun，et al.Information fusion technology and its application in INS/GPS/DVL integrated navigation［J］.Journal of Chinese Inertial Technology，2006，14(5):39-43.

［6］賴際舟，劉建業，劉瑞華.基于聯邦濾波的慣性導航姿態組合算法［J］.天津大學學報，2006，39(3):350-353.LAI Ji-zhou，LIU Jian-ye，LIU Rui-hua.Inertial navigation attitude-integrated method based on federated filters［J］.Journal of Tianjin University，2006，39(3):350-353.

［7］熊智，劉建業，郁豐.基于天文角度觀測的機載慣性/天文組合濾波算法研究［J］.宇航學報，2010，31(2):397-403.XIONG Zhi，LIU Jian-ye，YU Feng.Research of airborne INS/CNS integrated filtering algorithm based on celestial angle observation［J］.Journal of Astronautics，2010，31(2):397-403.

［8］LIEBE C C.Accuracy performance of star trackers-a tutorial［J］.Aerospace and Electronic Systems，IEEE Transactions on，2002，38(2):587-599.

［9］AFFREDO R，GMMUMN N，et al.Global Hawk-persistent，long range，high altitude，multi-int capability for the U.S.air force and the battlefield commander［C］.2003 AIAA/ICAS InternationalAir and Space Symposium and Exposition:The Next 100 Years.Dayton，hio，July 14-17，2003.1-6.

［10］PAPPALARDI F，DUNHUM S J，LEBLANG M E，et al.Alternatives to GPS［C］.OCEANS 2001，MTS/IEEE Conference and Exhibition，Hono.lulu，November 5-8，2001.

［11］KAPLAN G H.Determining the position and motion of a vessel from celestial observations［J］.Journal of the Institute of Navigation，1995，42(4):631-648.

［12］胡攀，高社生，倪龍強.UKF濾波在INS/無源北斗組合導航系統中的應用［J］.彈箭與制導學報，2009，29(5):69-72.HU Pan，GAO She-shen，NI Long-qiang.The application of UKF to INS/passive BEI-DOU integrated navigation system［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2009，29(5):69-72.

［13］陳永冰，鐘斌.慣性導航原理［M］.北京:國防工業出版，2007.