GPS 網基準兼容性的應變分析
白海明
(山西省地球物理化學勘察院,山西運城 044000)
GPS定位成果屬于WGS-84地心坐標系,而現今實用的測量成果屬于某一國家坐標系或地方獨立坐標系(參心坐標系),因此,實際工作中必須進行GPS網WGS-84坐標系成果至地面參心系的轉換。對于平面轉換,主要采用二維約束平差方法,即以地面網的已知點為約束條件,將GPS網強制附合到地面網中。我們知道,純GPS網具有較高的相對精度,而以往用傳統方法建立的地面網的相對精度卻難以與GPS網相比擬。就我國而言,傳統網存在分階段建立和分區平差等弊端,再加上長期地殼的不均勻運動,使得地面點間往往難以兼容一致。當采用一組一致性差的點為基準,進行GPS網二維約束平差時,必然引起純GPS網的扭曲變形,當這種變形不能容忍時,將極大地損壞GPS網的原有精度。因此,在進行GPS網二維約束平差時,進行基準點兼容性分析至關重要。分析GPS網基準兼容性的方法有多種,但大多對基準不兼容造成網的變形缺乏數量大小的概念和一定的幾何解釋。本文以基準點間的邊長為對象,把彈性力學中的應變分析方法應用到GPS網基準兼容性的叛定,可以很好地解決以往存在的問題。
1 基本原理及方法
1)彈性力學中變形與應變的基本概念和有關關系式。由彈性力學理論可知,彈性體在外力作用下,物體的各點的位置要發生變化,即發生位移。位移實際上由三部分組成,它們是參考點的剛體平移、剛體的轉動和純應變。前兩種位移后,仍保持各點間的初始狀態的相對位置,而純應變則改變了各點間的初始狀態的相對位置,即產生了變形。這里我們主要研究后一問題。
在假定介質是連續均勻、各向同性和小形變的情況下,可方便地對彈性體進行應變分析。在二維狀態下,彈性體內一點的純應變,可用其應變參數 εx,εy,rxy描述,其幾何意義為:εx,εy分別表示原來與X,Y軸平行的矢量單位長度的伸長(或壓縮),稱為線應變,伸長為正,縮短為負;rxy為變形前與OX,OY軸正向一致的兩正交線段在變形過程中發生的直角變化量,稱為剪應變,直角減小時為正,反之為負。
εx,εy,rxy的大小與坐標軸有關,在眾多的任意方向軸的應變中,存在著一對互相垂直的特殊方向,這對坐標方向存在最大和最小線應變ε1,ε2,其間的剪應變為0,稱主應變,并有以下關系式:

其中,r為總剪切;λ為總應變。
任意方向a上的線應變εa與該線段平均應變狀態分量之間的關系式如下[1]:

其中,D,D′分別為方向a上邊長變形前、后的長度;α為該邊方位角。
從式(5)可知,只要已知任意三個不同方向上的三個邊長D,D′及其方位角α,就可組成三個線性方程,從中解出三個應變參數εx,εy,rxy(當多于三邊時采用后述平差方法)。式(5)是本文進行應變分析采用的基本關系式。
2)利用已知點間邊長進行GPS網基準兼容性的應變分析原理和方法。
如前所述,GPS網轉換為地面坐標系時,常采用二維約束平差,實際上是將純GPS網強制附合到地面網中。如果將GPS網看作一彈性體,則地面網中已知點間平面邊長與GPS網中相應的平面邊長的差距,正是GPS網二維基準轉換時將引起的彈性變形量。因整個GPS網變形量的大小,歸根結底是由基準點間的變形來引起和決定的,若基準點間的變形量超過一定的限度,則整個GPS網的變形當然也就不可能容忍,因而,通過對基準點間邊長,根據式(5)求得的平均應變量也就能說明整個GPS網的變形狀態。如果對此應變量的大小加以恰當的限制,則可對基準兼容性進行叛定,這就是本方法的基本原理。
GPS網變形量限制條件可依不降低GPS測量精度為前提,同時滿足生產需要為基本準則。為此文獻[2]提出判定GPS網基準兼容性的兩個準則:
準則一:最大與最小線應變之差不應超過GPS基線測量精度的比例誤差:

準則二:最大線應變和剪應變也不應超過GPS基線測量精度的比例誤差:

準則一是對GPS網與地面網轉換時,變形量的均勻性要求,如果超過此限值,則GPS網將會產生較大扭曲,而準則二則是變形量大小的限制。
GPS網基準兼容性的應變分析步驟如下:
a.先進行GPS網的三維無約束平差,經各項檢驗合格后,再選擇與地面網相同的參考橢球元素和投影面,以及一致的中央子午線,并固定地面任意一已知點,進行GPS網二維自由網平差(或稱最小約束平差)。這時在二維平面內,純GPS網的尺度就與地面網保持一致,并且仍保持GPS網其原有的精度。
b.計算(或摘錄)已知的地面點間的高斯平面邊長D′和經二維自由網平差后,純GPS網中相應點間的高斯平面邊長D和方位角α。
c.采用不同的基準組合,以間接平差法,分別求解不同組合條件下的三個應變參數 εx,εy,rxy。
為實際應用方便,式(5)作如下變換:
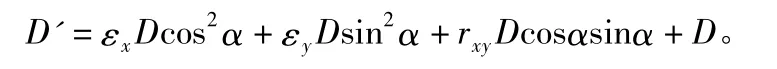
上式中把D作為非隨機量來進行處理。因一般純GPS網中邊長的精度是很高的,再加上D與D′相比具有現時性(不存在變形影響),這種處理不會引起應變參數太大的偏差,而能使計算簡化。
對于多條已知邊可以Di′為觀測值,列立如下誤差方程:
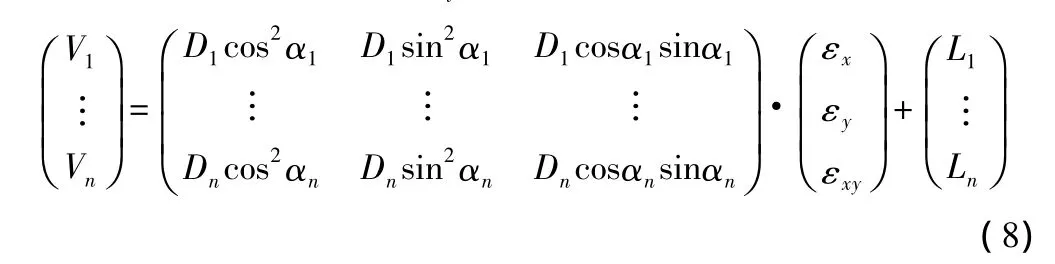
其中,Di以 km 為單位,Li=(Di-D′)/1 000(即 Li以 mm 為單位)。因D′的協因數陣往往不能直接給出,而一般情況下,邊長中誤差與邊長成正比關系,為此,簡便期間,D′的協因數陣可取如下對稱陣:

Qdd也可根據相應等級邊長相對精度分析給出。當已知邊長度及精度相近時,也可直接采用單位陣E。
根據式(8),式(9)即可按間接平差法求出參數 εx,εy,rxy,再據式(1)~式(4)算出其他參數。
d.根據求出的有關參數,以前述準則一、準則二為依據,分析判定基準點兼容性,從中選擇兼容性好的已知點組,參與GPS網的二維平差,獲得最終平差成果。
2 算例
如圖1所示為一實測D級GPS控制網。

圖1 D級GPS控制網
1,2,3,4為已知點,已通過各種方法判定其間一致性很好。為利用應變分析方法進行基準兼容性分析,現分別以兩種情況給2號,4號點加入不同的誤差進行分析對比。其中案例一給2號點坐標加入(3 cm,-3 cm)誤差,給4號點加入(-3 cm,3 cm)誤差;案例二給2號點加入(3 cm,-3 cm)誤差,給4號點加入(-5 cm,5 cm)誤差,分別計算其應變參數如表1~表3所示。
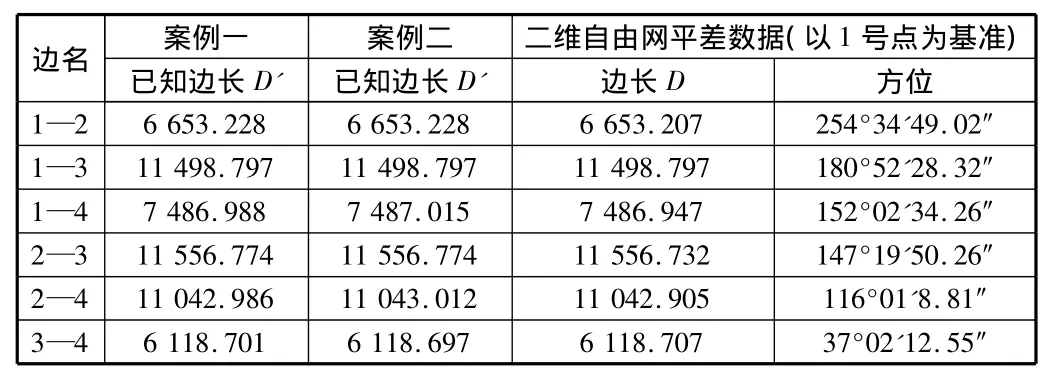
表1 計算用的基本數據表

表2 案例一不同基準組合下應變參數表

表3 案例二不同基準組合下應變參數表
因E級網的比例誤差為b=10 ppm,根據準則一、二及上述表2,表3可知:
案例一情況下,1—4組合方案均滿足要求,但以2方案為佳;而5組合方案總剪切較大,會使網產生較大扭曲,不可取。
案例二情況下,只有2方案滿足要求,其他方案均不可取。從表3可分析認為,4號點與其他點間不兼容,這也與前述假定是一致的。
3 結語
本文利用基準點間邊長進行GPS網基準兼容性的應變分析方法,既有數量概念,又有幾何意義,能夠對基準點不兼容而引起GPS網的變形有直觀的判斷和解釋,并且具有較強的靈敏度。特別適用于具有多個已知點時的檢驗分析。由于通常已知點個數總是有限,而所求參數只有三個,因而,誤差方程的組成和法方程的解算也就較為方便,不需要專用程序即可進行。上述算例的平差過程,就是筆者在Excel上實現的。通過實踐證明,本方法具有一定的可靠性和實用價值。
[1] 陶本藻.自由網平差與變形分析[M].武漢:武漢測繪科技大學出版社,2001:170-183.
[2] 張 勤,李家權.GPS測量原理及應用[M].北京:科學出版社,2005:174-212.
[3] 楊桂通.彈性力學[M].北京:高等教育出版社,1998.

