平面曲線輪廓與立體曲面的數控加工R參數化編程研究

楊順田

（四川工程職業技術學院，德陽 618000）

0 引言

在大多數情況下，先是由直線與圓弧構成的平面輪廓，再由平面輪廓、槽、孔等元素構成機器零件實體，加工過程中，又是在毛坯的基礎上以減少實體材料（金屬切削）的方式加工出零件的，因此，無論是什么數控系統都是以直線與圓弧作為基本的編程元素，如G01、G02、G03則是直線與圓弧的編程指令，若零件不是由直線或圓弧而是由非圓曲線構成的話，就無法用基本的編程指令完成編程。非圓曲線有許多種[1]，大體可分成能夠用數學表達的方程曲線如橢圓、拋物線、星型曲線等和不能用數學表達的列表曲線如蚌線、心臟線等。在此僅以能夠用數學表達的方程曲線構成的平面曲線輪廓與立體曲面進行數控加工R參數化編程的研究。

1 零件輪廓或曲面的插補處理及算法

1.1 插補處理

非圓曲線在進行數控編程之前，需要插補處理。所謂插補是指按一定的算法，計算出輪廓曲線上某些中間點坐標值的過程[2]即“數據密化”。從本質上講，插補處理也就是數學上連續曲線的離散化處理過程，它是將一個連續的曲線分割成若干個微小的線段，每段用直線或圓弧（即逼近線）去逼近輪廓曲線以此代替原有的非圓曲線，逼近線與輪廓曲線的交點或切點稱為節點。顯然，當節點的數量足夠多時，密化程度就越高，擬合出的曲線越光滑，所得到的輪廓曲線精度即插補精度就越高，但加工指令自然也就越長，降低了數控系統的運算速度，從而影響零件加工的效率，因此，數據密化的程度要適當。

離散化處理有多種方法。在數控加工離散化處理中，主要有積分插補法、數據采樣法、等誤差插補法與等距切片插補法等，但無論哪種方法，均以零件加工精度為標準。

1.2 列表曲線的插值計算

實際零件的輪廓形狀，除了由直線、圓弧或其他方程曲線組成的連續光滑輪廓之外，有些輪廓形狀是由實驗或測量獲得的若干數據點。通常，這些點是用表格形式給出的坐標點，由此形成的曲線常稱為列表曲線[3]，列表曲線形成的輪廓是非光滑的。為了獲得比較光滑的零件輪廓，常在兩個點之間插入一些點，稱為插值計算，常用的方法有牛頓插值法、二次樣條曲線擬合、圓弧樣條擬合等，目前常是用二次擬合法。

1.3 常用的算法研究

從逼近方法上看，常有兩種，即直線段逼近法與圓弧逼近法。所謂算法就是要根據不同的逼近方法找出節點的相應計算方法[4]，用直線段逼近非圓曲線，目前常用的節點計算方法有等間距法、等弦長法、等誤差法和等圓心角法；用圓弧段逼近非圓曲線，常用的節點計算方法有曲率圓法、三點圓法、相切圓法等。

圖1 四種逼近方式

1）等間距直線段逼近法：等間距法就是將某一坐標軸劃分成相等的間距，間距兩點之間用直線段代替原有曲線，如圖1（a）所示。等間距法的顯著優點是計算方便，特別適合于程序循環編程，其特點是在曲率半徑大小直接影響插補精度。2）等弦長直線逼近法：用長度相等的線段去逼近輪廓曲線，如圖1（b）所示，其優點是程序段的線段長度相等，缺點是插補誤差δ與曲率半徑R關系密切，且坐標值不易計算。3）“三點圓”圓弧逼近法：該方法是在等誤差直線段逼近求出各節點的基礎上，通過不在同一條直線上的連續三點作圓弧，用這樣的圓弧逼近非圓曲線，其缺點是要計算出圓心點坐標或圓的半徑值，計算困難且工作量大，如圖1（c）所示。對于無法用方程表示的列表曲線，利用“三點圓”圓弧編程指令CIP，編程可大大簡化，該方法具有明顯的優勢。4）等圓心角直線段逼近法：等圓心角法就是將某一弧線所對應的圓心角分成若干等分，每一等分圓心角（即步距角）所對應的弧用弦代替即“弦逼弧”。如圖1（d）所示。該方法的顯著優點是計算方便，特別適合于曲線方程變量為角度的情況，如橢圓、多邊形等輪廓的循環編程。除此之外，還有等誤差法直線段逼近法、相切圓圓弧逼近法等，它們各有優缺點。

2 采用成組技術構建同類零件的數學模型

利用事物間的相似性，將許多具有相似信息的研究對象歸并成組，并利用大致相同的方法去解決相似組中的生產技術問題，以達到規模生產的效果，這種技術稱為成組技術。在機械加工中，零件形狀相似，則制造工藝相似、數控程序相似[4]。對于能夠用數學表達的方程曲線構成的平面曲線輪廓或立體曲面，當其方程相同時，則其形狀相似，就可以構建同類或同族零件的數學模型即主樣件，再編寫主樣件R參數子程序并存貯于計算機中[5]。使用時，只需輸入具體零件實際參數，用實參代替形參，達到零件與程序的“一對一”效果，最后輸出該零件的數控加工程序。

3 平面曲線輪廓參數化編程

SINUMERIK R參數具有算術運算與邏輯運算的強大功能，還能夠運用C語言等高級計算機語言構成復雜的功能模塊，應用十分方便、靈活[6，7]。

如2圖所示的鍵槽零件族，可編制通用的R參數子程序，再通過主程序調用，實現鍵槽同族零件中任意鍵槽的加工，設參數R01=槽的長度，R02=槽的寬度，R03=槽的深度，R04=過度圓半徑，R05=刀具半徑，鍵槽R參數子程序如下：

JANCAO.SPF；鍵槽加工子程序

N05 G90 G01 X0 Y0；槽的中間先加工一刀（1-2點）

N10 G41 D02 X=-R04 Y=-（R02/2-R04）；建立刀補（2-3點）

N15 G03 X0 Y=-R02/2 CR=R04 ；圓弧切入（3-4點）

N20 G01 X=R01-R02 Y=-R02/2 ；加工下直邊（4-5點）

N25 G03 X=R01-R02 Y=R02/2 CR=R02/2；加工右半圓

N30 G01 X=0 Y=R02/2；加工上直邊（6-7點）

N35 G03 X=0 Y=-R02/2 CR=R02/2；加工左半圓（7-4點）

N40 G03 X=R04 Y=R04 CR=R04 ；圓弧切出（4-8點）

N45 M17

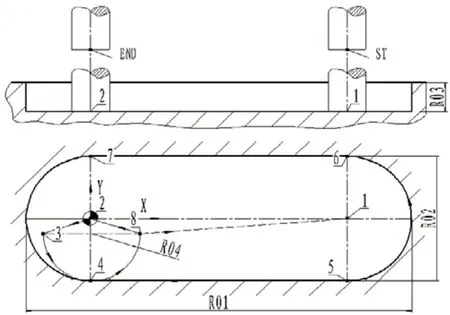
圖2 尺寸參數化的鍵槽零件族

加工某一鍵槽，其長度為120、寬度為70、深度15，則只需要對每個R參數賦值即可，若選用Φ32的鍵槽銑刀，則過度圓半徑取28，再調用鍵槽加工子程序，其主程序設計如下：

鍵槽加工主程序

DIAOYONG.MPF；調用子程序

N05 G90 G54 G00 X0 Y0 Z25；到達起始點

N10 M03 S600 F80；選取，下刀

N15 R01=120 R02=70 R03=15；給各R參數賦值

N20 R05=16 R04=25 JANCAO ；調用R參數子程序

N25 G00 Z25 M05

N30 M30

由此可見，只要有了同族零件R參數子程序，就可以加工同族中的每一個零件，無需“一對一”地去編寫每個零件的程序，極大地提高編程效率。

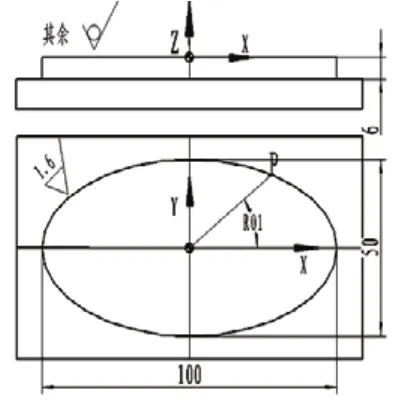
圖3 橢圓平面輪廓凸臺

現在分析平面曲線輪廓的參數編程，如圖3所示，它由橢圓構成的平面曲線輪廓凸臺零件，橢圓的參數方程是：X=R02*COS（R01），Y=R03*SIN（R01），其中R02為長半徑，R03為短半徑，R01為圓心角，用于控制插補精度與邊界：整橢圓0o～360o，四分之一橢圓0o～90o，應用參數及循環功能來編寫橢圓參數子程序，其關鍵點歸納為：

1）設定初始值，如下面程序片段中的N25；2）采用等圓心角直線段逼近法，步距角R01=1o控制插補精度，如N30；3）邊插補計算邊走刀加工，如N35；4）通過控制邊界判斷循環的結束。即N40程序段的“IF----GOTOB”循環條件控制語句。

程序片段如下：

……

N25 R01=0；初始角度為0

N30 MM：R01=R01+1；設定步長為1

N35 G01 X=R02*COS（R01）Y=R03*SIN（R01）；

計算坐標完成直線插補：

N40 IF R01<=360 GOTOB MM；循環判斷，直到等于360度與切入點重合

……

同樣，只要有了橢圓族零件R參數子程序，就可以加工一個任意尺寸的具體橢圓零件。

對于其他平面曲輪廓的R參數編程，均可采取類似的方法進行。

圖4 立體半橢球的曲面

4 立體曲面參數化編程

4.1 工藝分析

選題意義：圖4所示的零件，其外形是立體半橢球的規則曲面，它在三個軸線的截平面均為橢圓，體現出真正意義上的立體曲面，其參數編程具有通用性，典型性及推廣價值。

裝夾方案：可根據零件尺寸大小及實際情況選擇通用夾具或設計專用夾具進行工件的裝夾。

零件設定：XY坐標零點設在工件的中心位置。工件的上表面是執行刀具長度補償后的Z軸零點。

刀具選擇：視橢圓大小選用合適的平底鍵槽銑刀（粗加工）與球頭銑刀（精加工）加工橢圓外形輪廓，達到尺寸要求，銑刀半徑參數為R05，采用刀心編程，P點坐標等于輪廓尺寸加銑刀半徑。

4.2 編程思路

設R01、R02、R03分別是橢球XYZ各軸所對應的半徑，R05平底銑刀半徑，采用“刀心”方式編程，研究表明，橢球程序編制的四個關鍵步驟如下：

1）橢球如何分層及層數的循環與控制；2）每層橢圓的加工循環與控制；3）各軸的坐標計算；4）加工方向的確定。

由此可見，要用內外兩層循環才能實現立體半橢球的編程，外層循環R01控制橢球的層間循環，內層循環R02控制某一層橢圓的加工循環。

走刀路線可選擇逐層向下或逐層向上。從圖5中可以看出，無論哪種走刀，加工余量都是不均勻的，經過粗加工后，半橢球的大體形狀初步成形，余量不均勻狀況有所改善，采用逐層向下加工，開始加工的寬度余量較寬，需要較大直徑的刀具；采用逐層向上加工，開始加工的深度余量較深，需要較大刃長的刀具[8]，這就要根據橢球長短徑比來確定了，現采取逐層向上加工的方法編寫數控R參數子程序。

圖5 橢球上P點橢圓截面層

設P點為半橢球上的任意一點，過P點的水平截平面所截得的橢圓輪廓如圖虛線所示，在主視圖上是一條直線，另兩個視圖上的投影，如虛線橢圓（或半橢圓）所示，通過變量R01求得不同水平截平面所截得橢圓輪廓，不同層的橢圓由R01角度變量控制，步距角R01=1o，取值范圍為0o～90o，同一層橢圓輪廓的任意位置是K點，K的位置由R02變量控制，步距角R02=0.5o，取值范圍為0o～360o。

4.3 立體半橢球參數子程序

BANTUOQIU.SPF；立體半橢球的子程序名

N05 R01=0：R01層變量，從底層開始逐層向上加工

N10 KP1：R30=（R10+R05）*COS（R01）；計算P點X坐標

N15 R31=（R11+R05）*COS（R01）；計算P點Y坐標，

N20 R32=R12*SIN（R01）；計算P點Z坐標

……

N60 IF R01<=90 GOTOB KP2；外層循環結束，刀具到頂部

N65 Z=INC（10）；抬刀10mm

N70 RET；子程序結束

5 結論

平面非圓曲線輪廓特別是立體曲面的數控編程向來復雜，盡管可采用UG一類的編程軟件來解決，但畢竟都是針對某一個具體零件“一一對應”去編寫程序的，零件造型及生成的程序也只能用在某個具體的零件上，比較費工費時，而且成本又高，是一次性的，無重復使用可言！通過建立成組零件的參數模型，編寫成組零件的參數子程序，同組零件只需賦予相應的變量值，就可用同樣的R參數子程序加工，無需“一對一”地去編寫每個零件的程序，可以說是以“成組零件的參數子程序”的不變應“同組具體零件”的萬變的，一個參數子程序可無限次重復使用！極大地提高編程效率。

因此，該項成果具有積極的現實意義與推廣價值。

[1] 鞠華.逆向工程中自由曲面的數據處理與誤差補償研究[D].浙江大學.2003.

[2] 彭美武,楊順田.計算機數控技術[M].化學工業出版社.2011.

[3] 陳海舟.數控銑削加工宏程序及應用實例[M].機械工業出版社.2006.

[4] 蔡建國,許香穗.成組技術[M].機械工業出版社.1997.

[5] 周茂書.宏程序在數控編程中的應用[A].中國工程物理研究院科技年報(2000).2000.101-108.

[6] 吳大中.五軸聯動數控加工非線性誤差控制及后置處理[D].上海交通大學.2007.

[7] 楊順田.新編數控編程100例.從藍領走向金領[M].機械工業出版社.2011.

[8] 楊靜云,石玉寶.數控編程與工藝對橢圓曲面加工精度的影響[J].制造業自動化.2010.15.44-47.