基于慣性基準路形計系統特性分析

薛勁櫓，遲寶山，王紅巖，劉忠卿

（1. 裝甲兵工程學院 機械工程系，北京 100072；2. 西藏拉薩77626部隊41分隊，拉薩 851400）

0 引言

路面不平度測量裝置按測量基準不同分為固定基準裝置和隨動基準裝置；按是否與地面接觸可分為接觸式測量裝置和非接觸式測量裝置。基于慣性基準的路形計屬于隨動基準接觸式測量裝置，其結構簡單，幅頻特性優良，應用較為廣泛。

1 測量裝置系統簡化及振動分析

基于慣性基準路形計結構較為簡單，為便于分析，不考慮測試輪的動變形，忽略測試輪的剛度和阻尼，則儀器可簡化為一個單自由度振動系統，由質量塊、剛度和阻尼組成，如圖1所示。

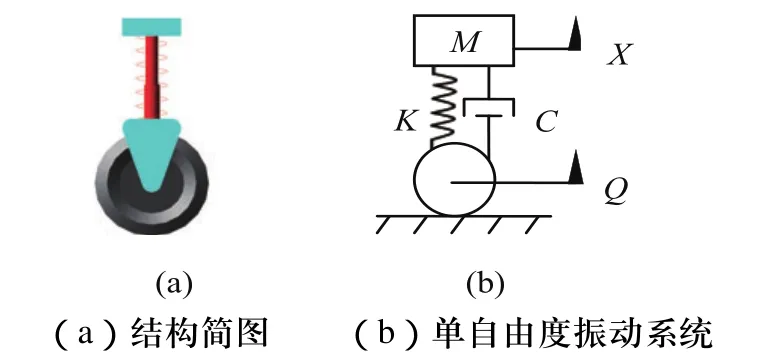
圖1 測試裝置簡圖

該單自由度系統的振動方程為：

該方程的解為有阻尼自由振動齊次方程的通解X1及非齊次方程的特解X2之和。

1.1 有阻尼系統自由振動

與式（1）對應的齊次方程的通解為：

1）欠阻尼（z＜1）

此時式（2）為：

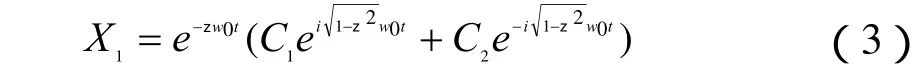
將式（6）代入式（4）可得系統自由振動響應。

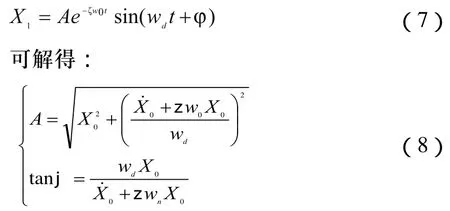
由式（8）可知，系統的振幅被限制在Ae?ζw0t和之內，并隨時間衰減，如圖2所示：

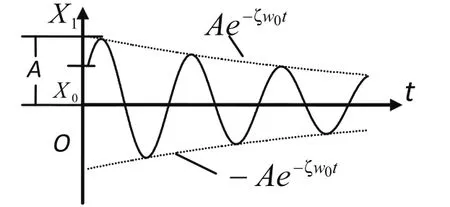
圖2 衰減的自由振動

2）臨界阻尼（ 1=z ）

式（2）變為：

由式（10）可知響應按指數規律衰減，如圖3所示：

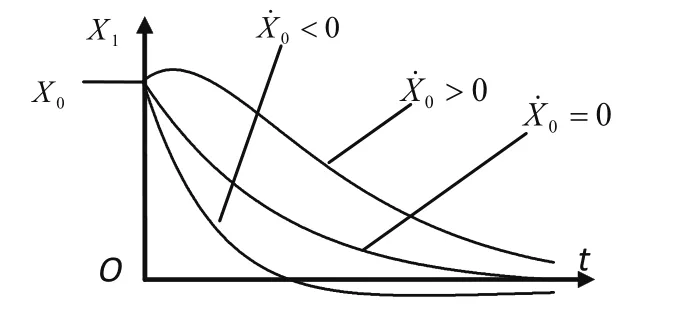
圖3 臨界阻尼情況

3）過阻尼（1＞z）

式（2）變為：

如圖4所示為初值 0)0( =X 、 1)0( =X˙ 時的響應曲線。

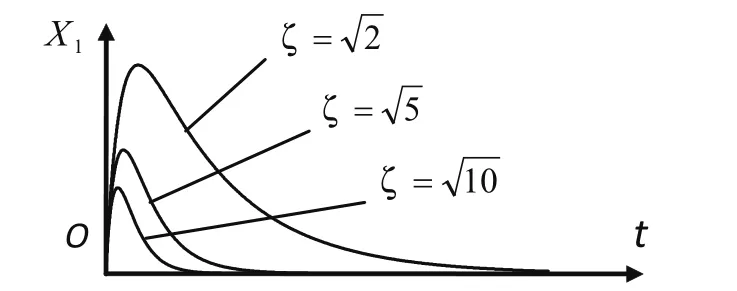
圖4 過阻尼情況

1.2 系統對路面不平度簡諧激勵的響應

單自由度系統振動方程（1）可寫為式（12）的形式，即變為一個強迫振動方程：

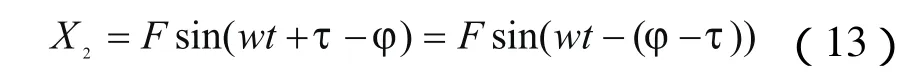
其中：F為簡諧激勵響應的振幅， )( tj- 為相位差，將式（13）代入式（12）得：

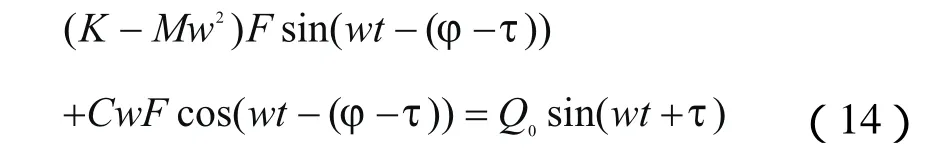
將上式右端改寫為：

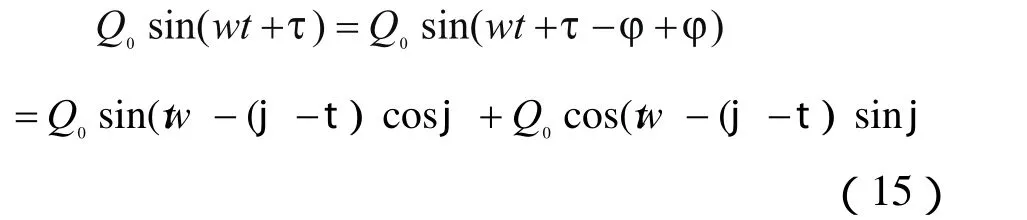
將式（15）代入式（14）得：

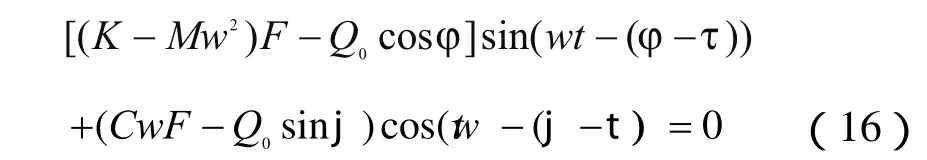
對于式（16），為使任意t時其值都為零，則：

由式（18）、（19）可知簡諧激勵的響應振幅和相位差只決定于系統本身的特性參數（C、M、K）、路面不平度激勵的幅值Q0與頻率w，與初始條件無關。

式（13）可寫為：

圖5為系統對簡諧激勵響應的幅值隨l變化的曲線：

圖5 響應的振幅特性曲線

由圖5可得如下結論：

3）當l接近于1時，系統與路面激勵產生共振，響應幅值達到最大，有阻尼系統的共振頻率為越大，共振頻率越小。

圖6和圖7為系統對簡諧激勵響應的相位隨l變化的曲線，圖6和圖7分別為路面的高頻和低頻部分：

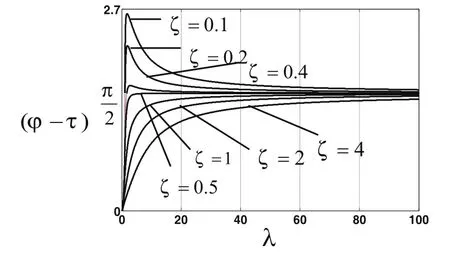
圖6 響應的相位特性曲線

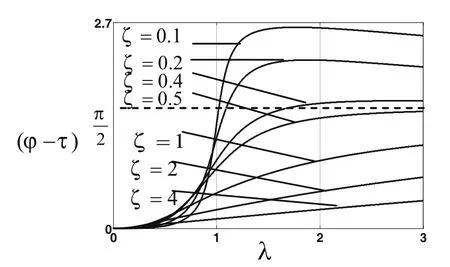
圖7 響應的相位特性曲線

由圖6和圖7可得如下結論：

1）l趨于無限大時，相位差趨近于 2/p ，即在路面高頻范圍內，響應幅值與路面激勵的幅值相差 2/p 個相位；2）l趨于零時，相位差趨近于零，即在路面低頻范圍內，響應幅值與路面激勵幅值趨近于同相。

2 測量裝置幅頻特性分析

頻響特性是路面不平度測量儀器最重要的性能指標，它決定了測量的可靠度。頻率響應特性包括幅頻特性和相頻特性，對基于慣性基準的路形計相頻特性不是很重要，所以本節主要分析系統的幅頻特性。

繪制系統的幅頻特性曲線，縱坐標為幅值比，橫坐標為路面頻率，設該系統的固有頻率如圖8所示為 z =0， z =0.1， z =0.4，時的系統幅頻特性雙對數坐標曲線。

由圖8可得以下結論：1)當路面激勵遠低于自振頻率時，系統的質量M和測量輪之間不產生相對運動，此時Q-X=0，系統的幅頻特性遠小于1，不能測量這樣低頻的路面諧波分量。2）當路面的激勵頻率遠高于自振頻率時，系統質量M的位移X=0，則Q-X=Q，幅頻特性為1，系統可較準確地測量路面不平度。3）路面輸入頻率在系統固有頻率附近時，出現峰值，如圖7所示。加大系統的阻尼比z可以有效消減共振。

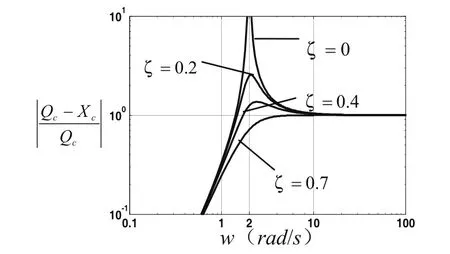
圖8 幅頻特性

3 測量波長范圍與測試速度關系

路面不平度是長度表示的空間域，在測量過程中通過速度將路面不平度空間歷程轉變為時間歷程。由于波長l與頻率w滿足 wvfv /2/ p l == ，當v分別取10km/h、20km/h和40km/h時（2.78m/s、5.56m/s和11.11m/s），l與w的關系曲線為：

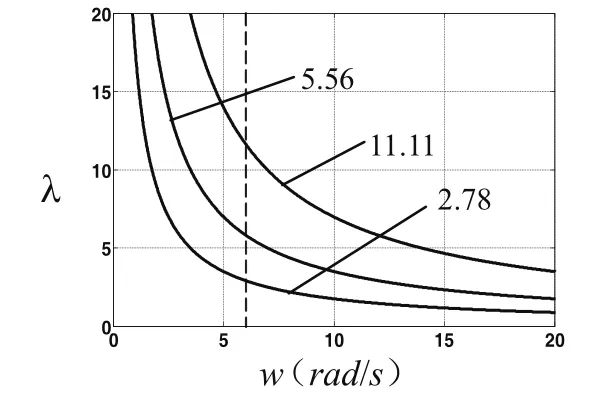
圖9 波長與頻率關系

表1 固有頻率固定

由表1可知：系統固有頻率一定時，適當減小阻尼比可增加儀器的波長測量范圍，且測量速度越高，可測量的最小波長越大。

3）當系統阻尼比一定時，根據式（29）可求出令系統幅值比為1的最小路面諧波頻率，代入式可求出對于不同車速的可測量最大波長。設阻尼比為 z =0.4。

表2 阻尼比固定

由表2可知：系統阻尼比一定時，適當降低系統固有頻率可增加儀器的波長測量范圍，且測量速度越高，可測量的最小波長越大。

4 結論

1）將基于慣性基準的路形計簡化為一單自由度振動系統，對其無阻尼自由振動以及在簡諧激勵下的強迫振動進行了分析。2）幅頻特性是路面不平度測量裝置最重要的性能指標，通過分析系統幅頻特性曲線可知，當路面激勵遠低于自振頻率時，系統的幅頻特性遠小于1，不能測量這樣低頻的路面諧波分量；當路面激勵頻率遠高于自振頻率時，幅頻特性為1，系統可較準確地測量路面不平度。3）對一系統特性參數固定的系統，測量速度越高，則可測的最小波長越大。4）對系統特性參數進行設計時，固有頻率一定，適當減小阻尼比可增加儀器的波長測量范圍；系統阻尼比一定，適當降低系統固有頻率可增加儀器的波長測量范圍。

[1] 石鋒,段虎明,楊殿閣,等.路面不平度的測量[J].武漢理工大學學報,2010,32(3).

[2] 段虎明,石峰,謝飛,等.路面不平度研究綜述[J].振動與沖擊,2009,28(9).

[2] 趙濟海,王哲人,關朝靂.路面不平度的測量分析與應用[M].北京:北京理工大學出版社,2000.

[3] 張義民.機械振動[M].北京:清華大學出版社,2007.

[4] 余志生.汽車理論[M].北京:機械工業出版社,2009.

[5] 劉新宇,肖傳宇,吳勇.慣性基準高程測量方法在路面平整度檢測中的應用[J].交通信息與安全,2009,27(5).

[6] 盧俊輝,巫世晶.基于車輪振動的路面實時識別研究[J].振動與沖擊,2008,27(4).