改進Kriging模型在固沖發動機導彈氣動優化設計中的應用①

楊 軍，劉勇瓊，艾春安，張 菲

(1.第二炮兵工程大學，西安 710025;2.中國航天科技集團公司四院四十三所，西安 710025;3.中國航天科技集團公司四院四十一所，西安 710025)

0 引言

導彈氣動問題具有高度非線性，且受限于CFD計算效率。因此，在其氣動優化設計研究中，無論是基于梯度信息的直接優化法，還是遺傳算法等現代智能非梯度優化方法，算法的收斂難度和速度均不滿足工程實際需要［1］。

近似優化技術本質上將便于計算的近似函數耦合到優化算法中，代替復雜的學科分析進程，多次迭代循環后，得到實際問題的近似最優解。Kriging模型由于適用于擬合高度非線性、多峰值的問題而廣泛用于飛行器氣動優化設計中。Shinkyu J等［2］將Kriging模型和遺傳算法相結合，對二維翼型進行了優化設計。張科施等［3］將Kriging模型和其他近似模型進行比較后，建立了基于近似技術的多學科設計優化框架，并用于高亞聲速運輸機機翼氣動/結構優化設計。許瑞飛等［1］將超立方抽樣試驗設計方法、EI方法、不斷更新的Kriging模型與優化方法結合，發展了基于改進Kriging模型的優化設計算法，并用于RAE2822翼型優化設計中。孫美建等［4］采用改進的量子粒子群算法，對Kriging模型的相關參數進行優化，并與具有雙層結構的粒子群算法相結合，對高維度、多目標、多約束的跨聲速機翼進行了優化。目前，國內還沒有將Kriging模型用于沖壓發動機導彈氣動優化設計中，且對該近似模型的擬合精度研究也不夠深入。

本文在深入研究相關參數θ對導彈氣動學科Kriging近似模型擬合精度影響的基礎上，基于最優相關參數將均勻試驗設計方法、Kriging模型與遺傳算法結合，提出了一種基于改進Kriging模型優化設計框架。將該方法用于固沖發動機導彈氣動優化設計中，優化后導彈的升阻比得到了極大提高，表明本文方法是可行的。

1 Kriging模型

Kriging模型中響應值與設計變量之間的關系可表示為

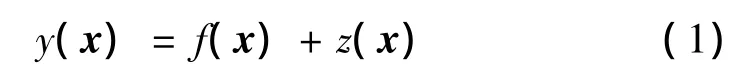
式中 y(x)為未知函數;f(x)為設計空間的全局模擬;z(x)為局部偏差。

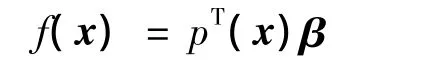
式中 pT(x)為多項式基函數組;β為系數向量。

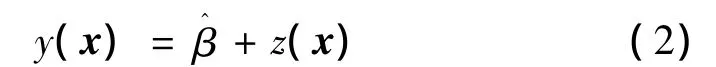
z(x)為隨機過程的實現，其統計特性為

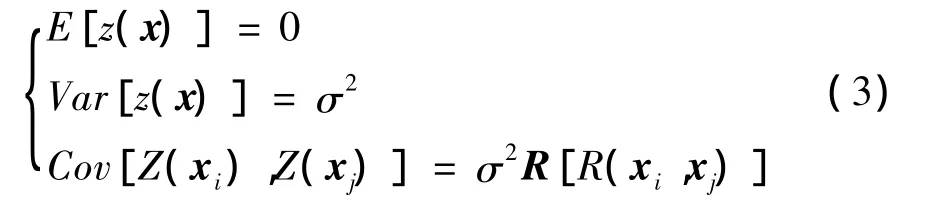
式中 R為相關矩陣;R(xi，xj)是任意兩樣本點xi、xj的相關函數。

R是n×n階對稱矩陣(n為樣本點個數)，相關函數的形式常用的有指數函數、高斯函數、樣條函數等，本文選取的高斯相關函數表達式為

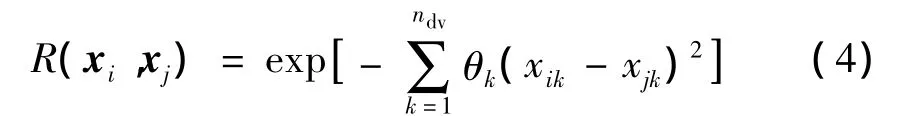
式中 ndv為設計變量個數;θk為未知的相關參數;xik、xjk是樣本點 xi、xj的第 k維元素。

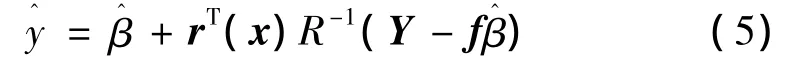
式中 Y為樣本點響應量矩陣;f為全1列向量;r(x)為樣本點和預測點之間的相關向量。

r(x)滿足:

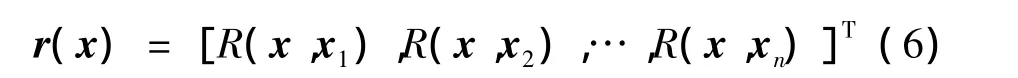
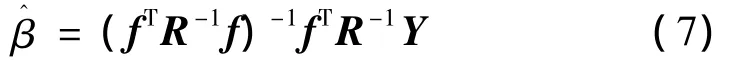
方差由式(8)求得:

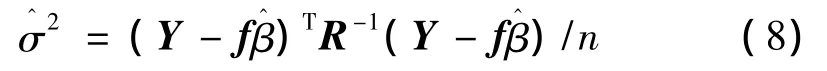
式(4)中的相關參數θk可由極大似然估計得到:

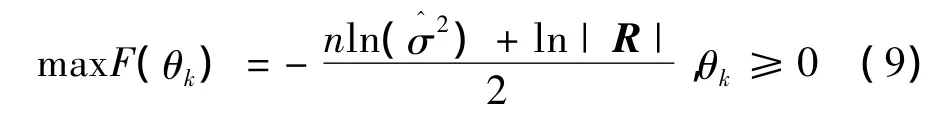
任意一組θk都能生成一個插值模型，但最優的θk能使得Kriging模型的預測精度最高，這需要求解式(9)的無約束非線性優化問題得到。

2 基于遺傳算法的最優相關參數

2.1 問題分析

本文基準導彈方案采用整體式固沖發動機、雙下側二元進氣道，2個彈翼和4個操縱尾翼呈X-X型正常式氣動布局。其典型縱向彈道可分為爬升段、巡航段和俯沖段。導彈巡航馬赫數為3，巡航高度10 km。根據不同外形參數對導彈氣動力系數的不同程度的影響，本文選取下述7個變量作為導彈氣動優化設計變量:導彈頭部長細比λn、彈翼展弦比λw、彈翼梢根比ηw、尾翼梢根比 ηT、彈翼后掠角 χw、尾翼后掠角 χT、進氣道唇口寬高比kn，各變量的取值范圍如表1所示。

2.2 遺傳算法(GA)求解

在Matlab下開發遺傳搜索算法源程序，求解導彈氣動優化問題的最優相關參數θ。同樣，用上述的21組數據作為構造Kriging模型的初始樣本點。遺傳算法主要參數:θ取值空間為［0，15］，初始種群規模為100，最大進化代數40。源程序模塊包括GA主程序、適應值函數計算模塊、優化結果輸出模塊。程序獨立運行10次，每一次均收斂良好且結果統一。圖2為升阻力系數最優相關參數θ的GA迭代收斂曲線。

表1 優化變量取值范圍Table 1 Range of the optimization variables

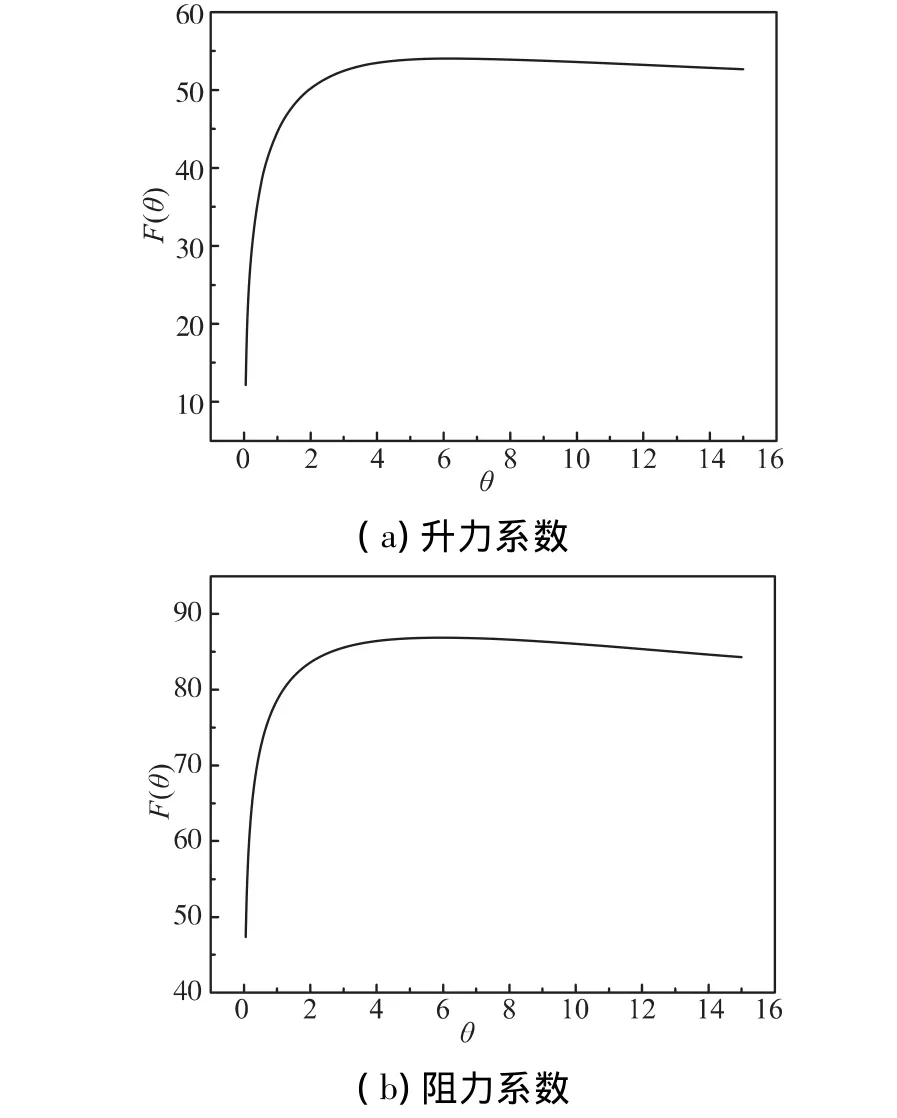
圖1 Kriging近似模型相關系數曲線Fig.1 The correlated parameters of Kriging approximate model

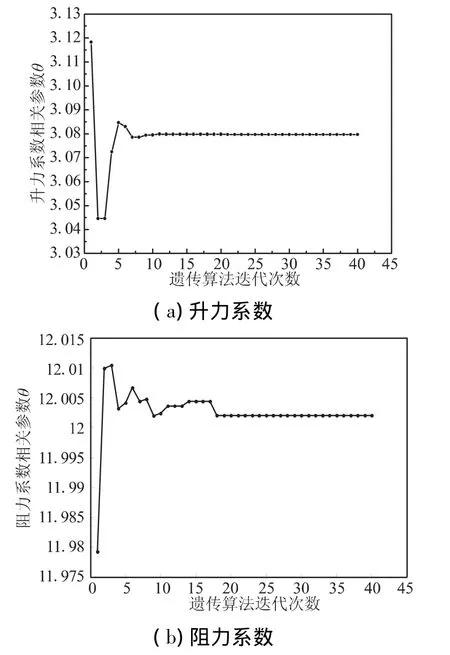
圖2 相關參數GA優化迭代歷史Fig.2 Correlated parameter＇s iterative history of GA

由上述結果可知，升力系數相關參數θ穩定收斂到最優解3.08，阻力系數相關參數收斂到最優解12.002，即對于本文的導彈氣動學科 Kriging近似模型，在上述21組初始樣本點數據基礎上，最優的相關參數 θ分別取3.08、12.002。

2.3 Kriging近似模型精度預測

為了驗證在最優θ取值條件下，Kriging近似模型對導彈氣動特性的預測能力，這里對氣動問題的擬合能力做了進一步檢驗。在隨機產生的20組預測樣本點條件下，分別用所建立的Kriging近似模型和Missile datcom精確分析模型計算導彈的氣動力系數，2種模型下升力系數、阻力系數比較如圖3所示，對應的該近似模型精度如表2所示，其中，e－為相對誤差均值，σe為相對誤差標準差，二者的具體定義可參考文獻［5］。

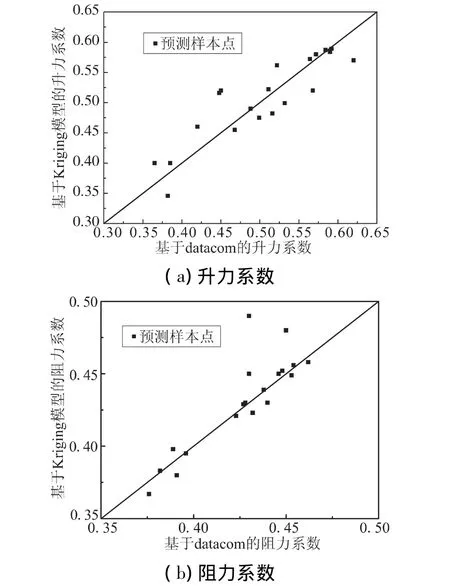
圖3 預測樣本點處氣動力系數比較Fig.3 Comparson of aerodynamic coefficients on predicted sample points

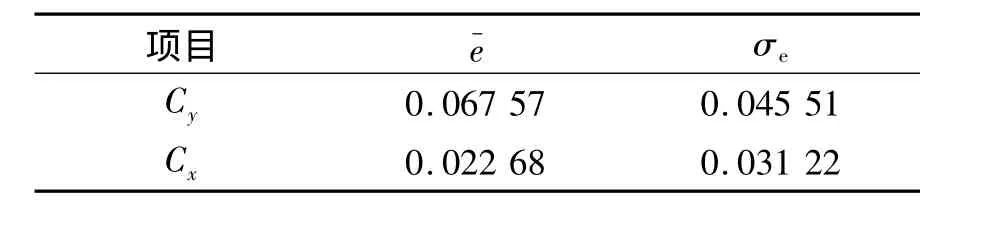
表2 預測樣本點處Kriging近似模型精度評估Table 2 Accuracy of Kriging approximate model on predicted sample points

綜上結果可見，盡管初始樣本點較少，但本文構造的用于固沖發動機導彈氣動優化的Kriging近似模型精度滿足要求，該模型能夠在一定精度范圍內替代比較耗時的氣動分析程序，并完成相關的氣動優化設計工作。

3 導彈氣動優化設計

3.1 基于改進的Kriging模型優化設計算法框架

本文在遺傳算法每次迭代中，都將上一代的最優個體信息加入到原有樣本集中，然后重新生成Kriging模型，這樣樣本點數量將隨著優化迭代不斷增加并更新，同時不斷接近最優解的臨域。圖4為基于不斷更新的Kriging模型的優化設計算法框架。

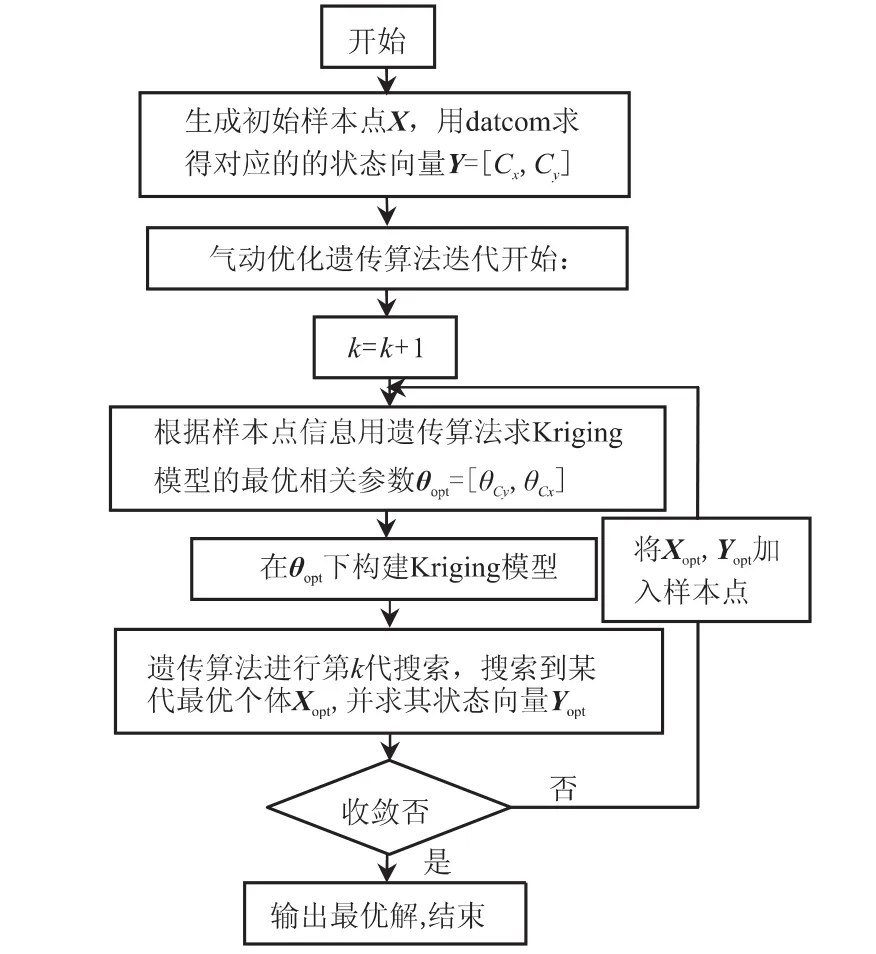
圖4 基于Kriging模型的優化設計算法框架Fig.4 Improved algorithmic framework based on Kriging approximate model

3.2 固沖發動機導彈氣動優化設計

根據圖4算法框架進行導彈氣動優化設計，采用遺傳算法尋找目標函數的最優值。以彈翼和尾翼面積作為約束條件，彈身最大橫截面面積保持不變，進行全彈最大升阻比優化設計。導彈飛行工況取巡航狀態:攻角2°，馬赫數 3.0，雷諾數 Re=5 172 612.76，優化問題可描述為

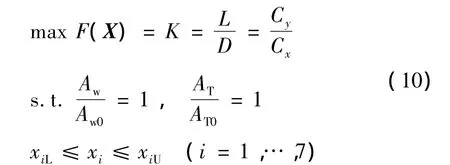
式中 K為升阻比;AW、AT分別為彈翼和尾翼面積;AW0、AT0分別為優化前導彈彈翼和尾翼面積;xiL和 xiU分別為設計變量取值上下限。

控制遺傳算法最大進化代數100，初始種群規模取300，GA迭代歷史如圖5所示。表3給出了優化前后導彈各氣動外形參數(即各設計變量)和升力系數、阻力系數、升阻比(即狀態變量)相對于原基準值的變化。

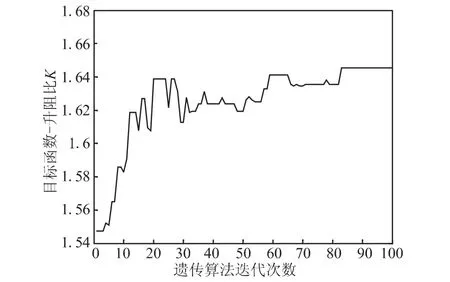
圖5 遺傳算法氣動優化迭代歷史Fig.5 Optimized iterative history of GA

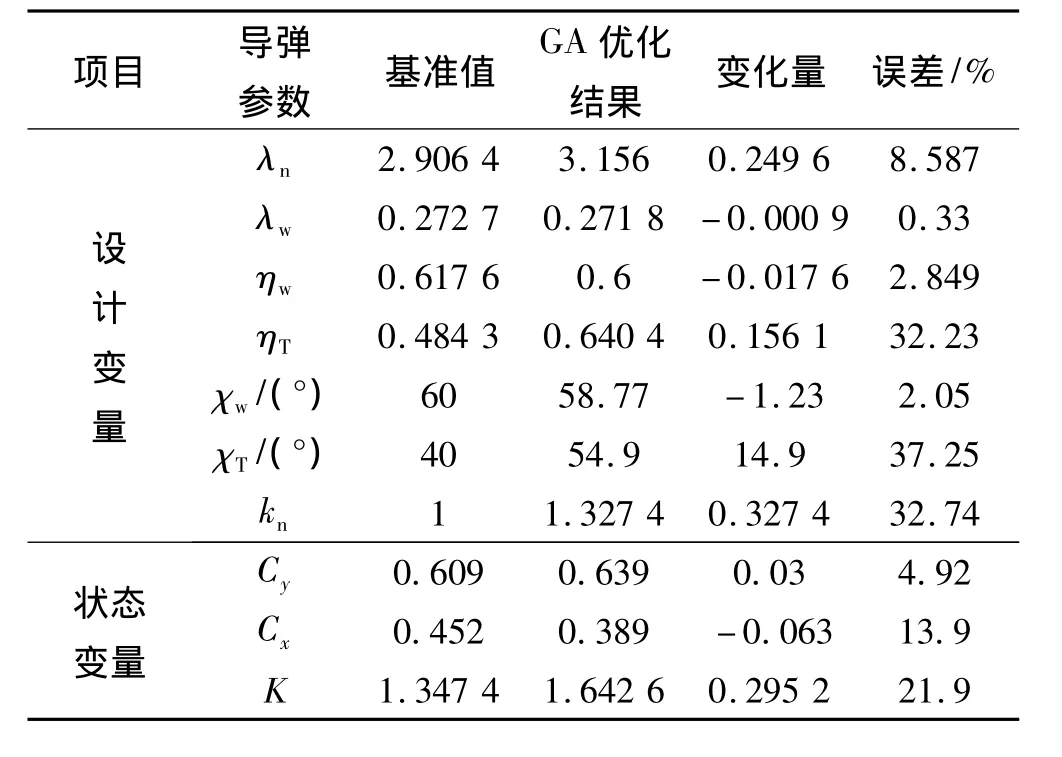
表3 導彈氣動優化設計結果Table 3 Results of aerodynamic optimization

由上述結果可見，本文采用的氣動優化算法穩定收斂。優化后彈翼和尾翼橫截面形狀均變化明顯，彈翼后緣掠角明顯增加，尾翼前后緣掠角均有很大增加，但梢根比有減小。另外，導彈頭部更加細長，這對減阻和氣動防熱設計均有利，進氣道本身相當于一個升力面，其入口寬高比也有增加。優化設計最終得到的方案下，全彈阻力系數下降了13.9%，而升力系數上升了4.92%，最終的升阻比上升達21.9%，且優化前后導彈彈翼、尾翼面積保持不變，優化設計的結果較好。

另外，隨著遺傳算法迭代次數的增加，越來越多的樣本點被加入到樣本集中，Kriging模型的近似精度也得到很大提高。同時，針對在最優解附近可能有多個相近峰值，GA求解獲得的最優群體一般分布于各個峰值附近，以上算法通過多次更新Kriging模型，也可避免漏選全局最優解。

4 結束語

(1)本文通過求解最優相關參數，對Kriging模型的擬合精度進行了詳細研究。結果表明，在樣本點個數受限條件下，通過搜索算法求得最優相關參數，可保證Kriging模型具有足夠的擬合精度。

(2)提出一種基于不斷更新Kriging模型的優化設計算法框架，并用于固沖發動機導彈氣動優化設計研究中，實現了導彈氣動性能的較大提高，對實際工程設計具有指導意義。

［1］許瑞飛，宋文萍，韓忠華.改進Kriging模型在翼型氣動優化設計中的應用研究［J］.西北工業大學學報，2010，28(4):503-510.

［2］Shinkyu J M M，K Y.Efficient optimization design method using Kriging［R］.AIAA 2004-118.

［3］張科施，韓忠華，李為吉，等.基于近似技術的高亞聲速運輸機機翼氣動/結構優化設計［J］.航空學報，2006，27(5):810-815.

［4］孫美建，詹浩.Kriging模型在機翼氣動外形優化中的應用［J］.航空動力學學報，2011，29(6):759-764.

［5］于劍橋，文仲輝，梅躍松，等.戰術導彈總體設計［M］.北京:北京航空航天大學出版社.2010.