關于動力總成懸置系統模態能量表達的一個注記

童 煒，侯之超

(清華大學，汽車安全與節能國家重點實驗室，北京 100084)

前言

汽車動力總成是汽車主要的振動和噪聲源。動力總成懸置設計的好壞，直接影響著整車的NVH性能。有效的懸置設計，不但要求合理設定系統的各階固有頻率大小，而且也須盡可能解除振動耦合［1-9］。對于依據剛體-彈性支承模型建立的6自由度動力總成懸置系統方程，可定義6×6階模態能量分布矩陣［1-5］。動力學仿真軟件ADAMS因其直觀性與強大的功能，正日益廣泛地應用于懸置的優化與分析［6，8-9］。它引入了6×9階能量分布矩陣，并給出各分量的簡單計算式。迄今，尚未見文獻明確闡述兩種能量表示方式之間的關系。這不利于ADAMS軟件在動力總成懸置設計中的推廣應用。

本文中首先回顧了基于彈性支承空間剛體動力學建立的動力總成懸置系統方程，介紹了能量解耦方法及其所定義的能量分布矩陣。在應用ADAMS軟件進行動力總成懸置系統自由振動分析的基礎上，給出了其中所定義的能量分布矩陣元素的計算式。通過對比分析，闡述了兩種能量分布矩陣之間的差異與關系。最后通過某款汽車的動力總成懸置系統對有關結果予以驗證。

1 系統動力學方程及模態能量

1.1 系統動力學方程

動力總成隔振設計的基本理論是彈性支承空間剛體動力學。其中，將包括發動機、離合器和變速器在內的動力總成簡化為剛體，懸置軟墊簡化為線彈性彈簧。圖1為一個4點懸置支承的動力總成系統示意圖。圖中，坐標系x軸與曲軸中心線重合，正向指向發動機前端，z軸與氣缸軸線平行、正向垂直向上，y軸由右手法則確定。通常，固定坐標系GXYZ和隨體坐標系o-xyz原點均在質心處，靜平衡狀態下二者重合。

忽略懸置膠墊的阻尼，系統作自由振動的微分方程為

式中:M、K分別為質量矩陣與剛度矩陣;q為廣義位移向量;l為懸置個數;ki為懸置i的3向剛度矩陣;D、O分別為懸置位置與安裝角定義的變換矩陣。

1.2 基于模態能量的振動解耦

從能量角度來看，振動耦合就是沿著某個廣義坐標方向施加的力或力矩所做的功轉化為系統在多個坐標方向的動能和勢能。對于保守系統，機械能守恒。因此任一階主振動的總能量可用最大動能或最大勢能表示。

多自由度振動系統作第n階主振動的最大動能為

式中:ωn與Xn分別為系統的固有圓頻率與對應主振型向量。將式(2)展開，并定義第i個廣義坐標上的動能及其在總能量中的百分比分別為

式中:(Xn)k(k=i，j)表示振型向量的第k個分量;Mij為質量矩陣中第i行j列的元素。的大小表示能量集中程度，若其值為100%，則說明系統第n階主振動的能量全部集中在第i個廣義坐標方向，而其它廣義坐標方向的振動為零，這就實現了振動解耦。工程實際中，由于布置空間和成本等方面的限制，難以在6個廣義坐標方向都實現振動解耦(即完全解耦)。因此，現代汽車動力總成懸置設計通常采用部分解耦，特別是在激振能量大的方向上要保證解耦。

1.3 模態能量分布矩陣

考察在任一主振動中各坐標方向上的能量分布。依據式(3)和質量矩陣的定義可知，3個平動坐標方向的能量為

3個轉動坐標方向上的模態動能分別為

式(5)為系統第n階主振動時沿x、y和z方向的平動能量分量。式(6)～式(8)則分別表示系統轉動能量分量，每項均包含繞坐標軸純轉動和繞平面轉動兩個部分。對式(1)所示6自由度動力總成懸置系統方程，分別對各階主振動依據式(5)～式(8)計算，帶入式(4)最終得到一個6×6階模態能量分布矩陣，稱為基于自由度的模態能量分布矩陣。

2 ADAMS建模過程及模態能量

將CAD軟件建立的動力總成三維幾何模型導入ADAMS/View后，輸入動力總成的慣量參數和懸置軟墊的彈性與阻尼參數，參數化后即可完成系統動力學建模。在ADAMS中，將系統分成若干子系統，分別計算各個子系統的能量，求和得到系統的總能量。設系統被分成k個子系統，第n階主振動時系統總的模態能量可表達為

顯然每個能量分量均表示對慣性張量某分量的貢獻。其中:式(11)代表子系統質量的影響，對應沿廣義坐標x、y和z方向的平動能量;式(12)～式(14)代表子系統轉動慣量的影響;式(15)～式(17)則代表子系統慣性積的影響;兩組元素分別對應繞廣義坐標x、y和z軸的一部分轉動能量。

依據式(9)和式(11)～式(17)，子系統第e個能量分量在該階主振動總能量中的百分比為

分別對6階主振動進行計算即得到一個6×9階矩陣，可稱為基于慣性參數的能量分布矩陣。

3 兩種能量表達式的對比

應用ADAMS軟件進行動力總成懸置系統自由振動分析時，將發動機、變速器和離合器等視為一個剛體，通常不計入支架、車身等結構的影響。這樣整個系統只有一個子系統，即j=1。

對比式(5)～式(8)與式(11)～式(17)可知

在以上各式中已應用慣性張量的對稱性，即Jxy=Jyx，Jyz=Jzy，Jxz=Jzx。依據這組關系式可確定式(4)與式(18)所示能量百分比之間的對應關系。

顯然，式(5)～式(8)所定義的能量分量，因與自由度對應，故物理意義更為明確。另外，ADAMS軟件在定義模態能量分量時，在保持平動能量分量不變的同時，將與轉動相關的3個能量分拆成6個彼此更為簡單而無交叉的分量，以分別描述轉動慣量或慣性積對系統主振動能量的貢獻。這樣更易于反映系統各慣性參數的影響。

由式(19)～式(22)可知，式(9)和式(10)定義的總的模態能量(j=1)與式(2)完全一致。這是由模態能量的物理意義決定的。

不難理解，式(6)～式(8)或式(20)～式(22)給出的能量值及其百分比可能小于零。在工程應用中，為避免負值能量與模態動能概念之間的不協調，可取絕對值計算能量分量、能量和與能量百分比［7］。但這種處理后，分布矩陣元素均為正值，總能量會偏大，各元素值也異于不取絕對值得到的結果。

4 算例及分析

某款汽車的動力總成采用4點懸置，其基本參數見表1～表3。

基于式(1)在Matlab中直接編程，或應用ADAMS(2005版)仿真，可得系統的固有頻率，見表4。

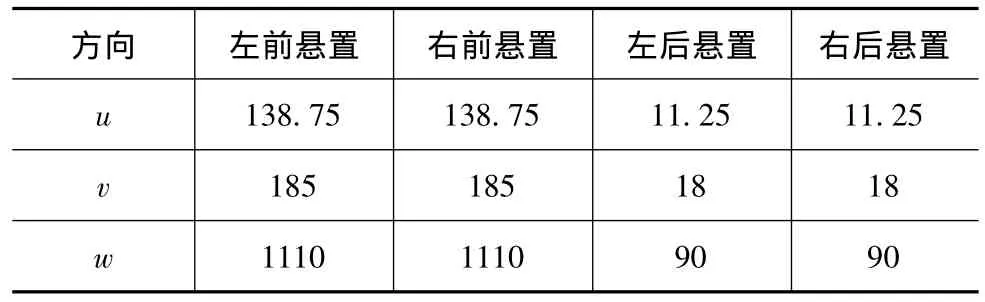
表1 懸置軟墊3向靜剛度值 N/mm

表2 總成質量與慣量

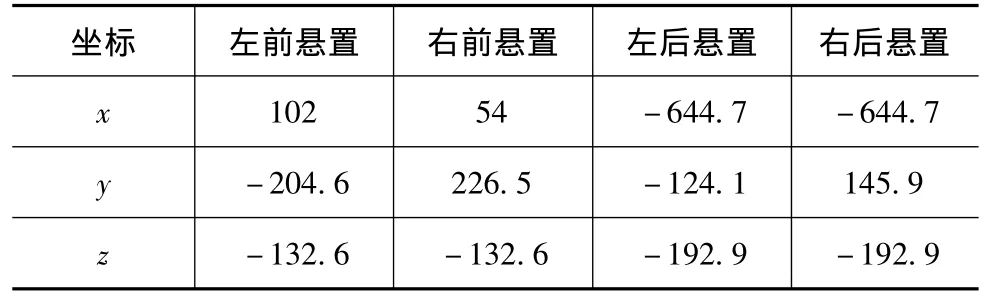
表3 懸置軟墊安裝位置坐標 mm

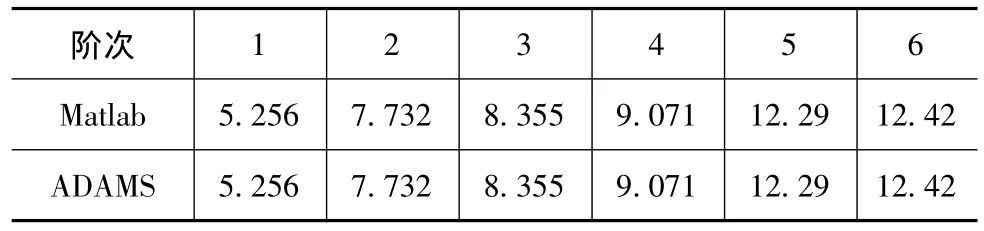
表4 系統固有頻率 Hz

由表4可見，應用Matlab編程得到的頻率與ADAMS仿真計算結果相同。

應用各自得到的主振型矩陣，分別依據式(4)～式(8)或式(9)～式(18)，同時考慮是否取絕對值，可得到相應的能量分布矩陣，X、Y、Z分別表示純平動能量，RXX、RYY、RZZ分別為繞坐標軸純轉動能量，RXY、RXZ、RYZ則為慣性積引起的平面交換能量，見表5和表6。其中表6所示結果分別由Matlab與ADAMS計算得到。

由表5和表6可知，基于自由度的能量分布矩陣與基于慣性參數的能量分布矩陣中，均因慣性積的存在而出現了負值能量。取絕對值后計算的模態能量總和稍稍增大，各元素也相應地發生改變，但是不影響對主振動能量在各自由度或慣性參數上分布的定性判斷。另外無論是否取絕對值，式(19)～式(22)所示關系均能得到滿足。

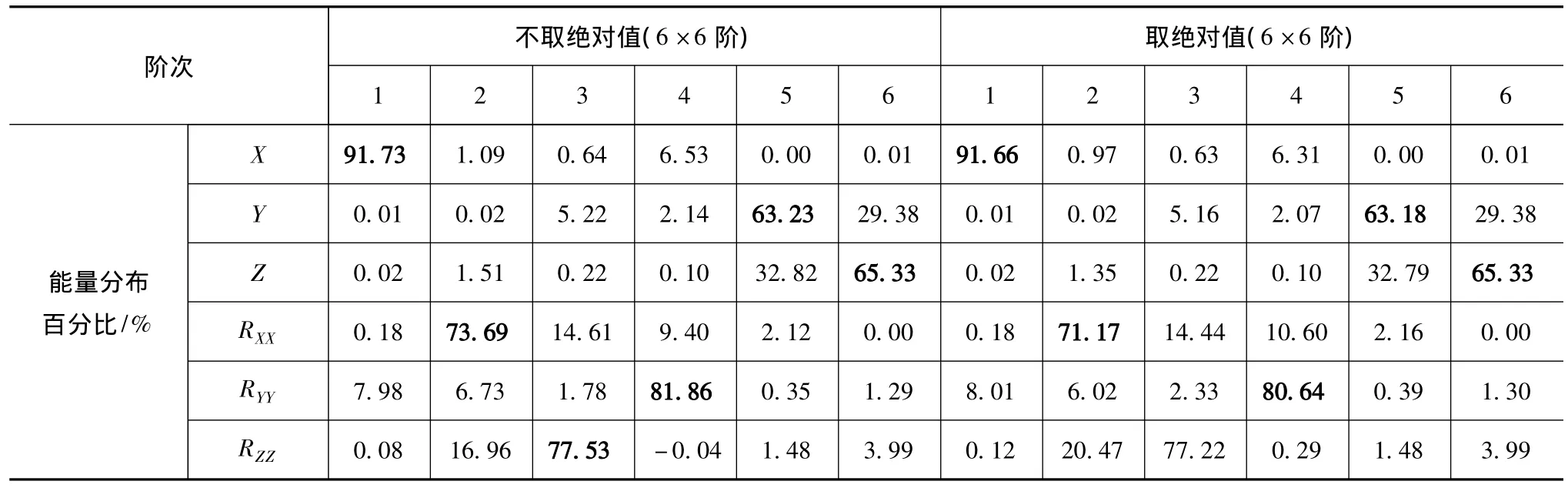
表5 基于自由度的能量分布矩陣

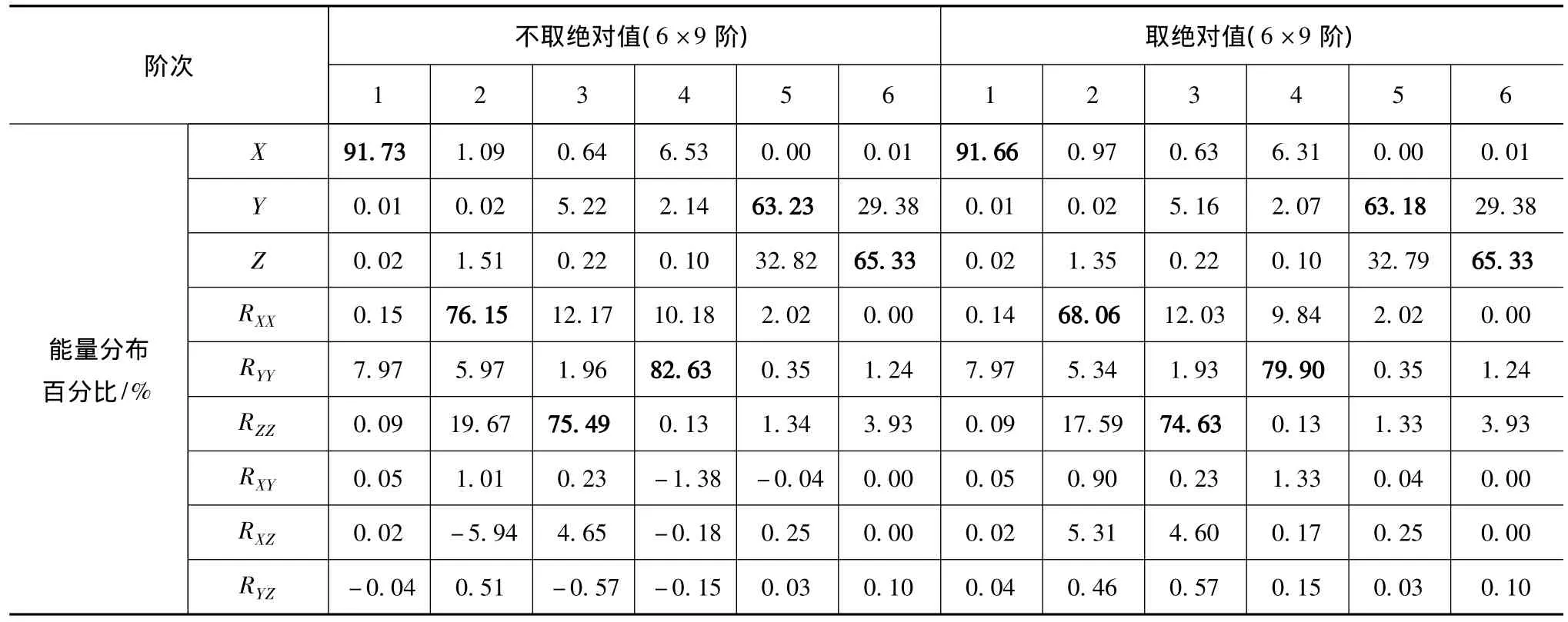
表6 基于慣性參數的能量分布矩陣

5 結論

(1)基于系統自由度而定義的6×6階模態能量分布矩陣，體現了主振動中振動能量在系統各自由度上的分布情況，物理意義明確、便于理解。

(2)ADAMS中定義的6×9階能量分布矩陣，與系統自由度并不對應，但是能夠更明確地反映慣性張量中不同元素的影響。

(3)兩種模態能量分布矩陣，取絕對值計算得到的能量分布與依據基本定義得到的結果不同，但仍能準確地反映出主振動能量在各自由度或慣性參數上的分配情況。

(4)對于任一階主振動，無論是否取絕對值進行計算，兩種表達方式給出的模態能量總和相等、平動能量也彼此相等;描述轉動的對應能量分量之間均滿足模態動能定義所決定的對應關系。

［1］徐石安，肖德炳，鄭樂寧，等.發動機懸置的設計及優化［J］.汽車工程，1983(3):12-23.

［2］上官文斌，蔣學鋒.發動機懸置系統的優化設計［J］.汽車工程，1992，14(2):103-110，119.

［3］閻紅玉，徐石安.發動機懸置系統的能量解耦法及優化設計［J］.汽車工程，1993，15(6):321-328，334.

［4］徐石安.汽車發動機彈性支撐隔振的解耦方法［J］.汽車工程，1995，17(4):198-204.

［5］Cho Seonho.Configuration and Sizing Design Optimization of Powertrain Mounting Systems［J］.International Journal of Vehicle Design，2000，24(1):34-47.

［6］方錫邦，陳樹勇，張文炬.轎車動力總成懸置系統隔振性能的仿真研究［J］.合肥工業大學學報(自然科學版)，2003，26(2):236-241.

［7］范讓林，呂振華.剛體-彈性支承系統振動解耦評價方法分析［J］.工程力學，2006，23(7):13-18.

［8］王顯會，李守成，黃鵬程，等.轎車發動機動力總成懸置系統優化研究［J］.南京理工大學學報(自然科學版)，2006，30(1):17-20.

［9］李令兵，陳劍，吳趙生.基于ADAMS的發動機懸置系統設計［J］.噪聲與振動控制，2007(6):42-44，48.