水平線性互補(bǔ)問題中常用矩陣對及其性質(zhì)

王秀玉， 申海明， 李 琳

0 引 言

給定矩陣M，N∈Rn×n和向量q∈Rn，水平線性互補(bǔ)問題 HLCP（M，N，q）為:求向量x∈Rn和y∈Rn，使其滿足:

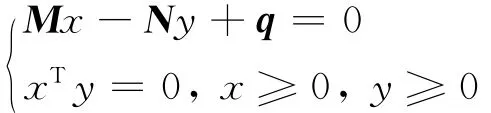
水平線性互補(bǔ)問題產(chǎn)生于經(jīng)濟(jì)平衡問題、非協(xié)作競賽、交通分配問題和優(yōu)化問題中，因此在實(shí)際中有重要應(yīng)用。文獻(xiàn)［1-3］分別對單調(diào)和充分矩陣對所對應(yīng)的水平線性互補(bǔ)問題進(jìn)行了研究。為獲得水平線性互補(bǔ)問題的可解性及數(shù)值解，有必要研究水平互補(bǔ)問題中的矩陣對（M，N）的性質(zhì)，矩陣對（M，N）的性質(zhì)決定著水平互補(bǔ)問題解的存在性、有界性。但現(xiàn)有資料中只給出了正定矩陣對的定義，其它矩陣對還很少有學(xué)者考慮。文中就研究半正定矩陣對、P＊－矩陣［4］對以及更廣泛的擬P＊－矩陣對和P（τ，α）-矩陣對，并給出它們的等價定義。

1 半正定矩陣對及P＊－矩陣對等的性質(zhì)

定義1 M，N為n×n矩陣，若對任意的u，v∈Rn，（u，v）≠0，滿足 Mu＝Nv，有uTv＞0，則稱（M，N）為正定矩陣對。正定矩陣對即為文獻(xiàn)［2-3］中的單調(diào)矩陣對。

例1

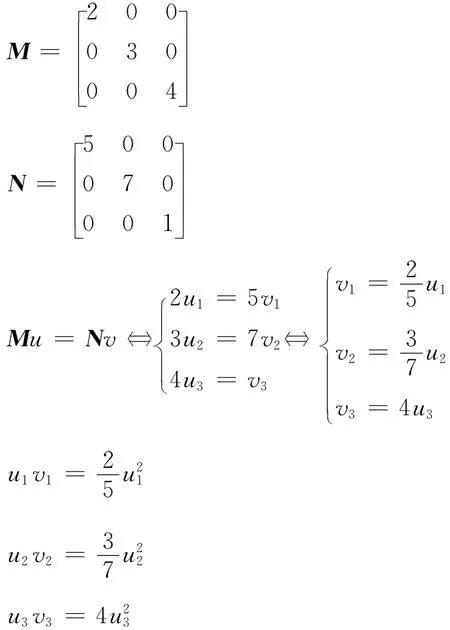
則（M，N）為正定矩陣對。

定義2 M，N為n×n矩陣，若對任意的u，v∈Rn，（u，v）≠0，滿足 Mu＝Nv，有uTv≥0，則稱（M，N）為半正定矩陣對。

例2

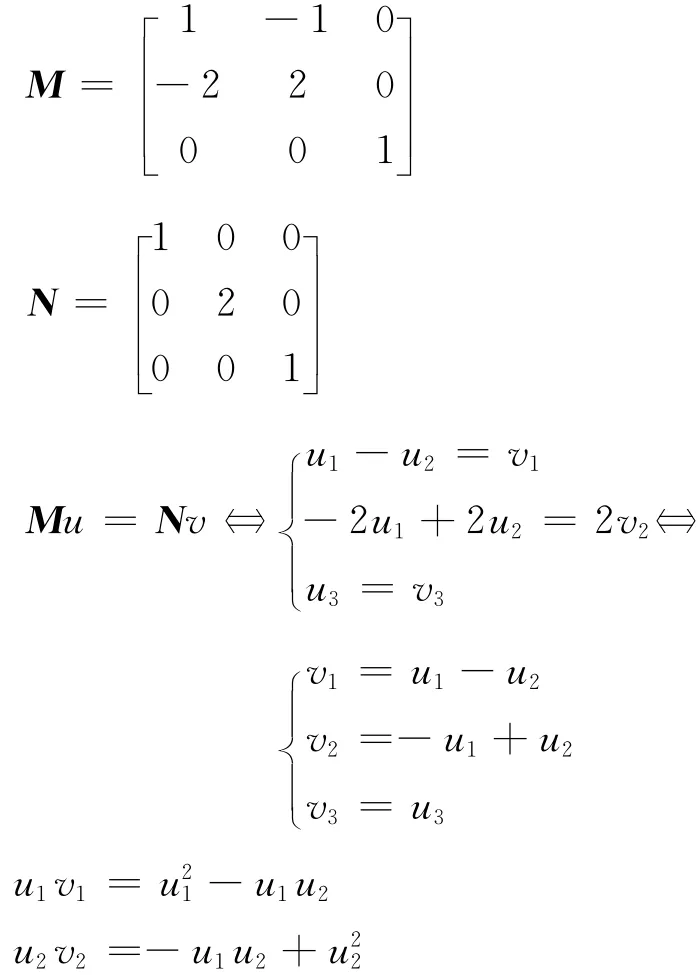
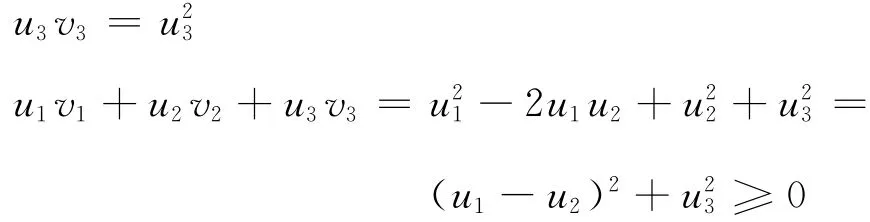
則（M，N）為半正定矩陣對，但不為正定矩陣對。

定義3 M，N為n×n矩陣，若對任意的u，v∈Rn，（u，v）≠0，滿足 Mu＝Nv，有則稱（M，N）為P-矩陣對，顯然正定矩陣對必為P－矩陣對。

例3

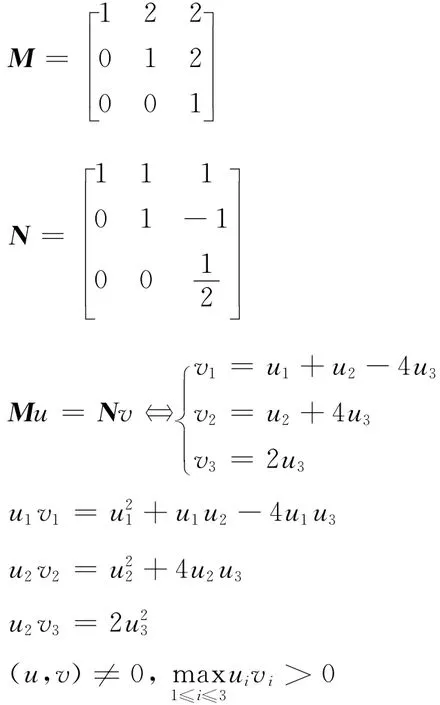
因此（M，N）為P-矩陣對，但不為正定矩陣對，如u1＝2，u2＝0，u3＝2，uTv＜0。

定理1 （M，N）為正定矩陣對?M為正定矩陣。即對?u∈Rn，u≠0，有uT（Mu）＞0。

定義4 M，N為n×n矩陣，若對任意的向量u，v∈Rn，（u，v）≠0，滿足 Mu＝Nv，存在常數(shù)τ≥0，使得

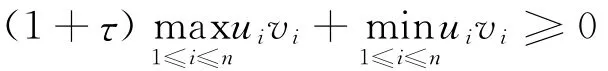
則稱（M，N）為P＊-矩陣對。

例4

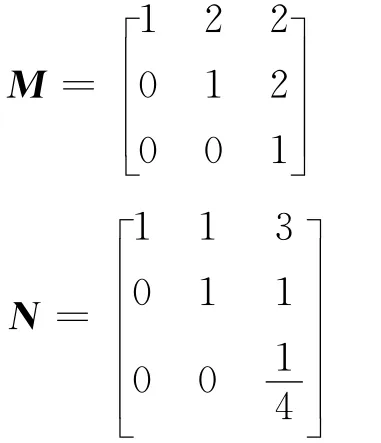
定義5 M，N為n×n矩陣，若對任意的u，v∈Rn，（u，v）≠0，滿足 Mu＝Nv，有則稱（M，N）為P0－矩陣對，顯然P-矩陣對必為P0－矩陣對。

例5

因此有

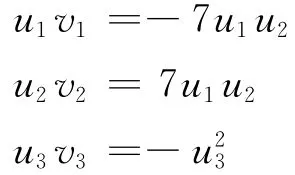
例6

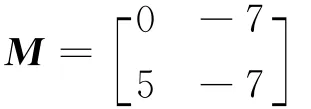
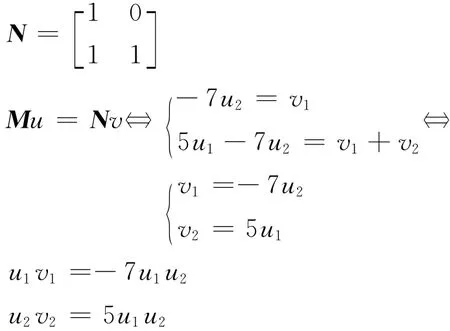
定理2 正定矩陣對（M，N）為P-矩陣對，則必為P＊－矩陣對。

證明 若（M，N）為P-矩陣對，對?u，v∈Rn，

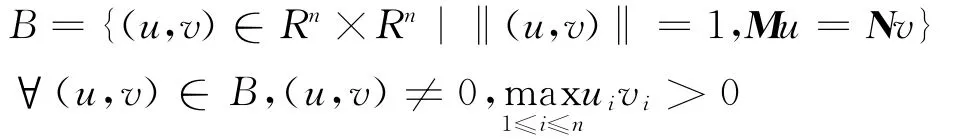
考慮函數(shù)

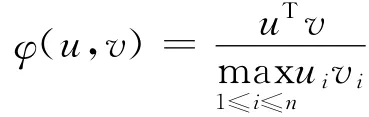
φ（u，v）在B 上連續(xù)，因此

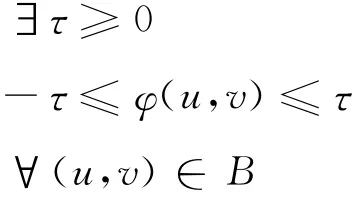
即

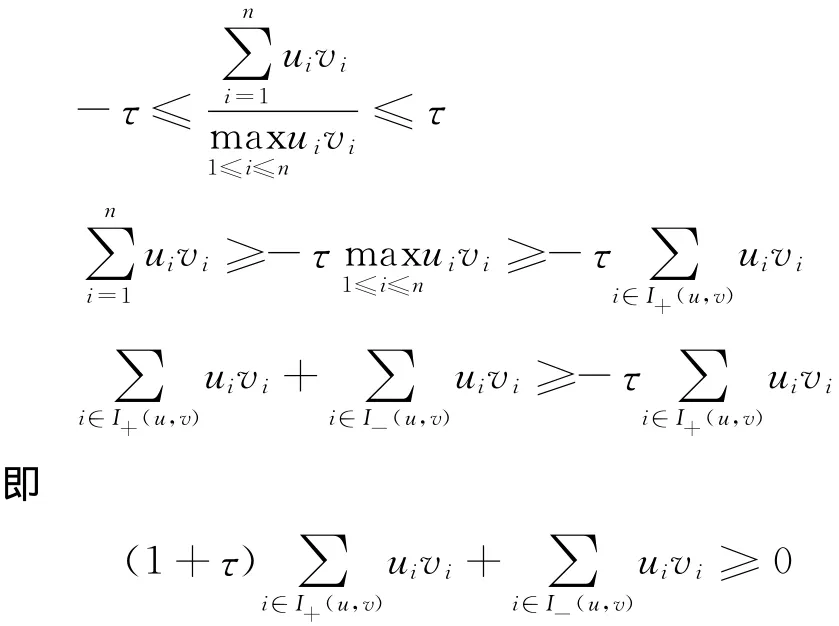
其中

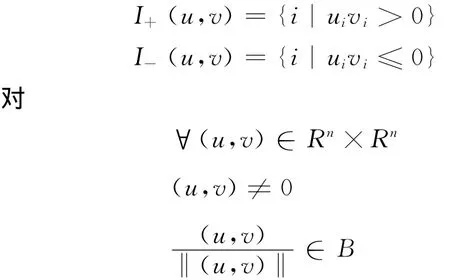
證畢。

定理3 （M，N）為P＊-矩陣對??τ′＞0使得

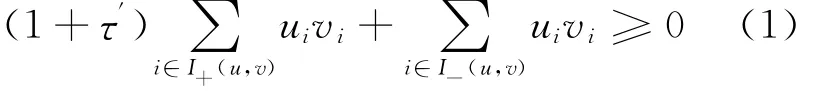
證 對任意的

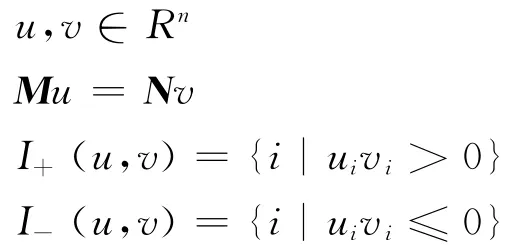
若（M，N）為P＊-矩陣對，則有

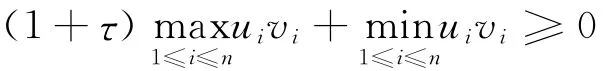
情形（1）:I＋（u，v）＝／○，其中，／○為空集，即（1）成立。

情形（2）:I＋（u，v）≠／○，即，只需考慮I-（u，v）≠／○，取

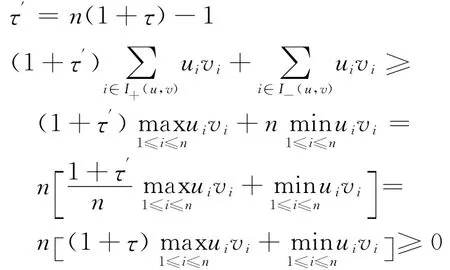
即式（1）成立。

反之，若式（1）成立:

情形（1）:I＋（u，v）＝／○，由式（1）uivi＝0，i＝1，2，…，n，因而對?τ≥0，

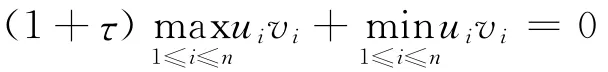
情形（2）:I＋（u，v）≠／○，只需考慮I- （u，v）≠／○，取

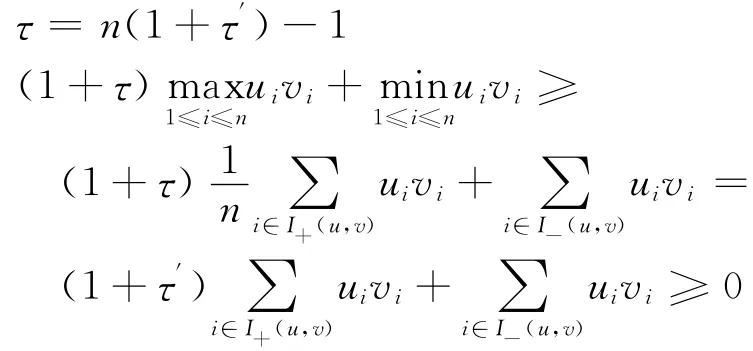
證畢。

定義6 M，N為n×n矩陣，若對任意的u，v∈Rn，（u，v）≠0，滿足Mu＝Nv，存在τ≥0，α≥0，使得

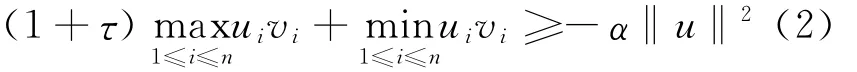
則稱矩陣對（M，N）為P（τ，α）-矩陣對。顯然，P＊－矩陣對必為P（τ，α）-矩陣對。

例7

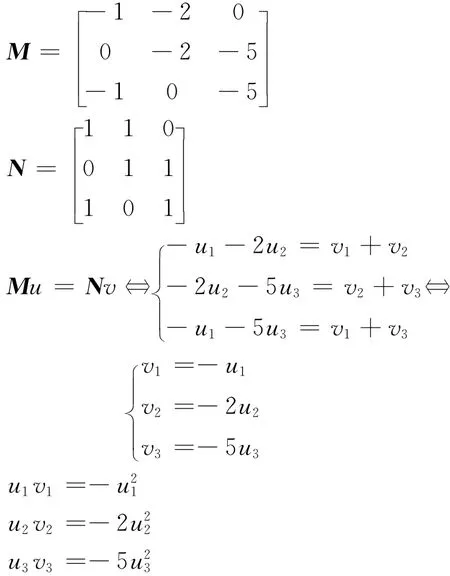
（M，N）不為P0矩陣對。

為使

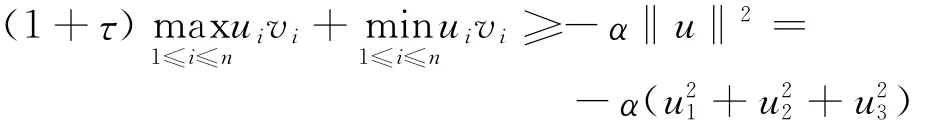
取τ＝0，α＝5，即

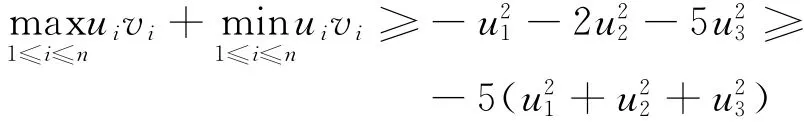
即（M，N）為P（τ，α）-矩陣對。

定理4 （M，N）為P（τ，α）-矩陣對當(dāng)且僅當(dāng)存在常數(shù)τ′≥0，α′≥0，使得

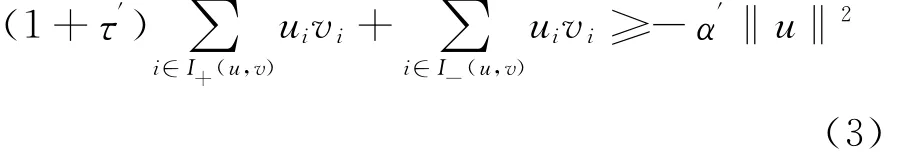
其中

I＋（u，v）＝ ｛i｜uivi＞0，Mu＝Nv｝

I- （u，v）＝ ｛i｜uivi≤0，Mu＝Nv｝

證明 對任意的u，v∈Rn，且Mu＝Nv，若（M，N）為P（τ，α）-矩陣對［5］，即有式（2）成立，分兩種情形討論。

情形（1）:I＋（u，v）＝／○，即（2）得，uivi＝0，i＝1，2，…，n，對任意的τ′≥0，式（3）成立。

情形（2）:I＋（u，v）≠／○，只需考慮I- （u，v）≠／○，取

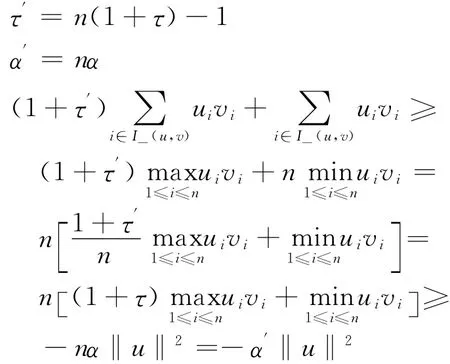
反之，若式（3）成立，也分兩種情形討論，取

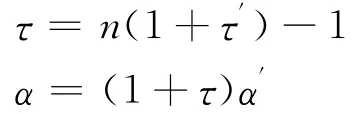
情形（1）:

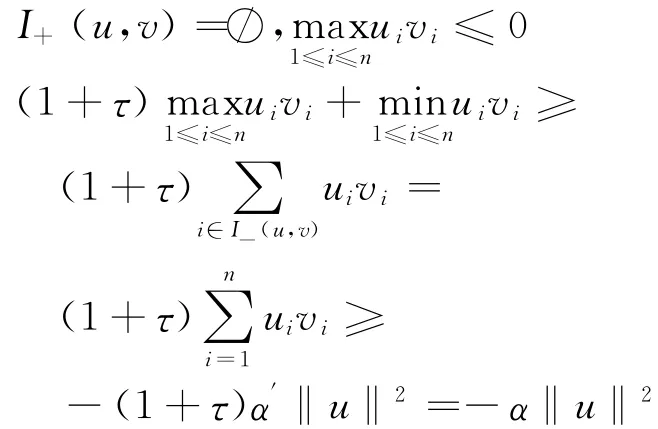
情形（2）:I＋（u，v）≠／○，只須考慮

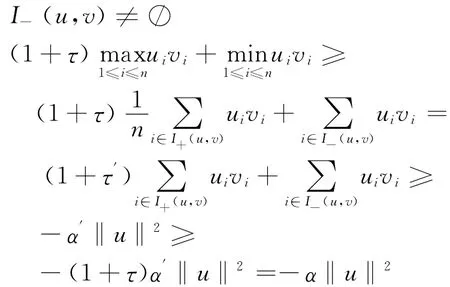
2 P＊－矩陣對水平互補(bǔ)問題解集的凸性

記

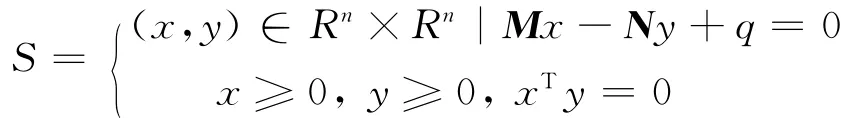
定理5 若 （M，N）為P＊－矩陣對，則S為凸集［6－8］。

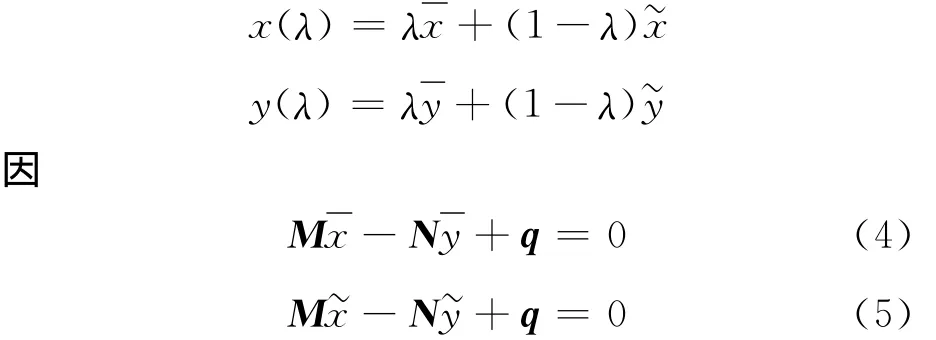
從而有

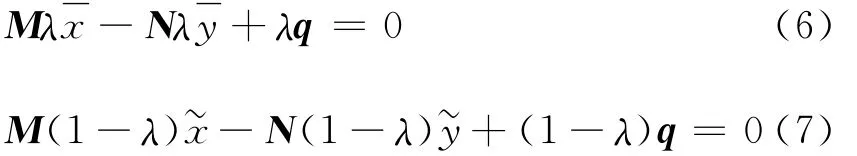
式（6）＋式（7）得

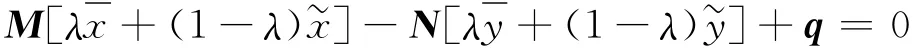
又由于

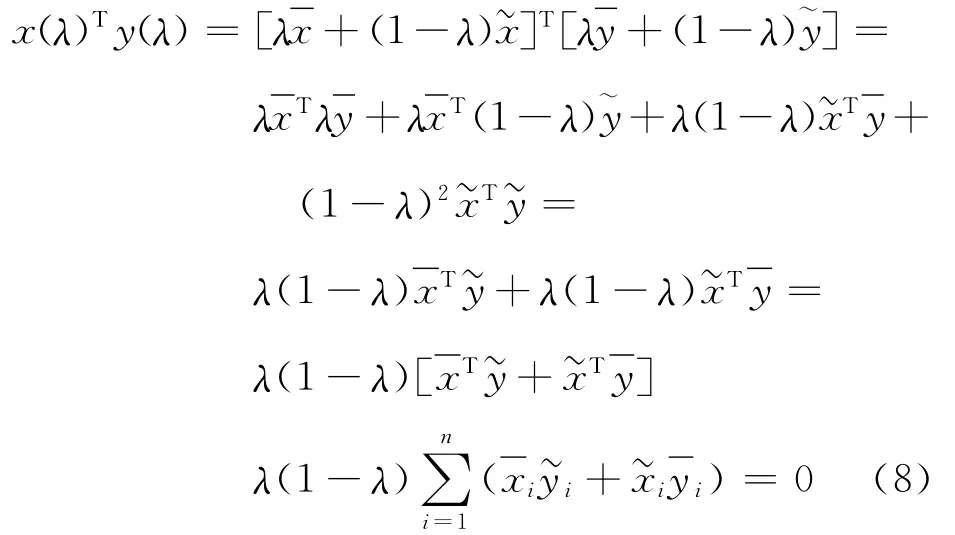
事實(shí)上，式（4）－式（5）得

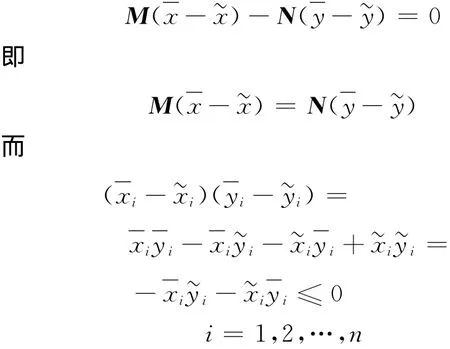
若存在下標(biāo)i，使得

而（M，N）為P＊-矩陣對，必有

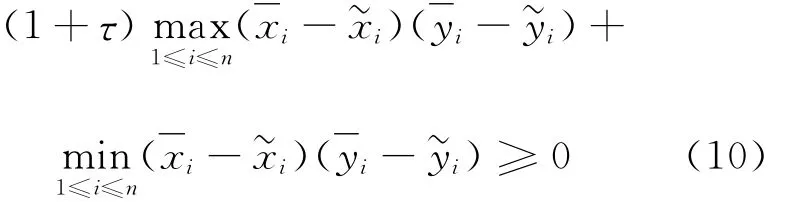
式（9）與式（10）矛盾，因此，對i＝1，2，…，n均有

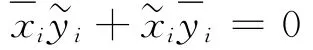
由式（8）知，（x（λ），y（λ））∈S，證畢。

［1］ Filiz Gurtuna，Cosmin Petra，F(xiàn)lorian A Potra.Corrector-predictor methods for sufficient linear complementarity problems［J］.Comput Optim Appl.，2011，48:453-485.

［2］ Gowda M S.On the extended linear complementarity problem ［J］.Mathematical Programming，1996，72:33-50.

［3］ Gowda M S.Reducing a monotone horizontal LCP to an LCP［J］.Applied Mathematics Letter，1995，8（1）:97-100.

［4］ Hannu Valiaho.P＊-matrices are just sufficient［J］.Linear Algebra and its Applications，1996，239:103-108.

［5］ 徐俊彥，苗壯，譚佳偉，等.解線性互補(bǔ)問題的組合同倫方法［J］.長春工業(yè)大學(xué)學(xué)報(bào):自然科學(xué)版，2010，31（3）:269-274.

［6］ 高興寶.解水平線性互補(bǔ)問題的神經(jīng)網(wǎng)絡(luò)［J］.西安石油大學(xué)學(xué)報(bào):自然科學(xué)版，2004，19（1）:85-88.

［7］ 孫洪春.求解水平線性互補(bǔ)問題的一個非光滑二次收斂算法［J］.四川師范大學(xué)學(xué)報(bào):自然科學(xué)版，2007，30（5）:136-138.

［8］ 林正華，盛中平.預(yù)估－校正算法跟蹤組合同倫路徑［J］.計(jì)算數(shù)學(xué)，2002，24（4）:405-416.