靜電場中高斯定理的證明

付 靜， 姜廣軍

（吉林建筑工程學院城建學院 基礎部，吉林 長春 130111）

0 引 言

高斯定理的證明一般有3種方法［1］：

1）利用電場線模型，先從點電荷位于球面內球心處的特例來證明高斯定理，然后再推廣到任意的閉合曲面。這種方法相對比較簡單，但是從特例推廣一般情況不夠嚴謹；

2）利用立體角的概念證明高斯定理，此方法雖嚴謹，但要求學生具有豐富的空間想象力，難度較大；

3）應用電場強度概念和純數學推導證明高斯定理，這種方法非常繁雜和抽象，且物理含義不清晰。

1 電場強度通量的概念

借助于電場線的圖像，引入電場強度通量的概念［2－4］。通過任意一曲面的電場強度通量如圖1所示。

必須指出，對非閉合曲面，面法線的正方向可以取曲面的任一側，對閉合曲面來說，通常規定自內向外的方向為面積元法線的正方向，所以，在電場線從曲面之內向外穿出處，E通量為正；反之，在電場線從外部穿入曲面處，E通量則為負。

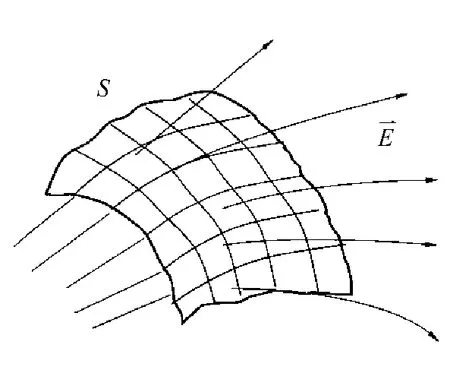
圖1

2 高斯定理的證明

2.1 正點電荷在球面中心

在正點電荷q激發的電場中，通過以點電荷為中心、半徑為r的球面上的E通量如圖2所示。

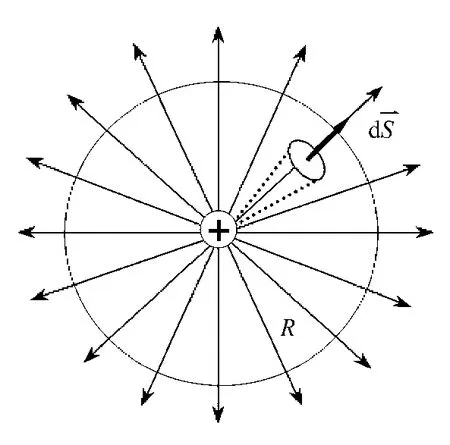
圖2

利用庫侖定律，在球面上任一點的電場強度為

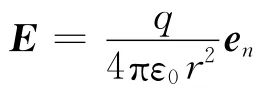
利用式（1）可求得通過該閉合球面上的E通量為：

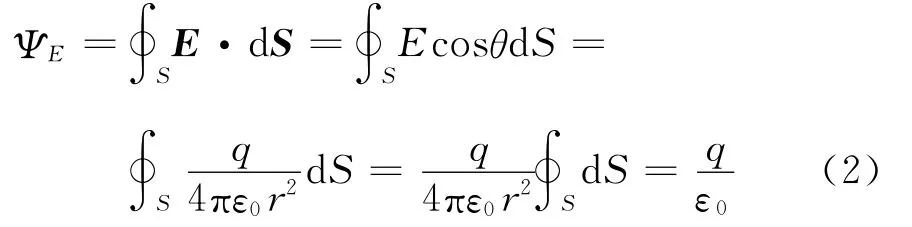
2.2 正點電荷不在球面中心（或任意閉合曲面內）

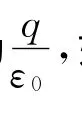
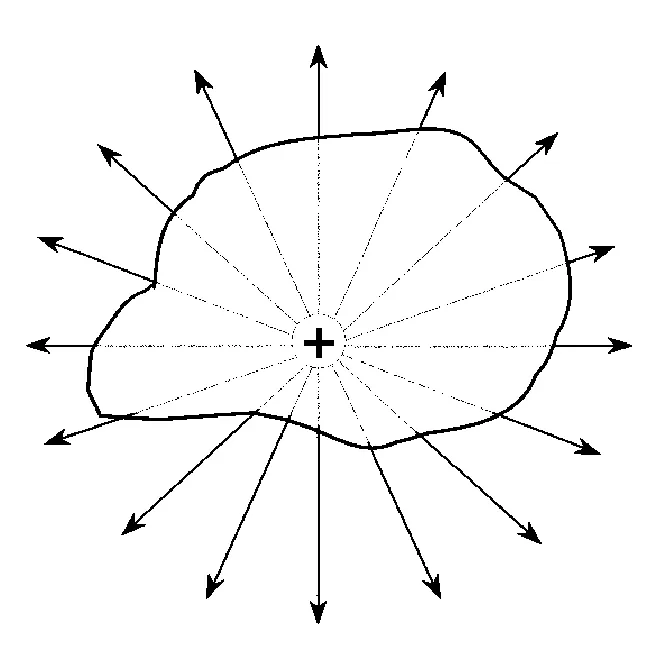
圖3

2.3 多個正點電荷在閉合曲面內

如圖4所示，n個電荷在閉合曲面內，根據電場強度疊加原理，空間任一點的電場強度是這n個電荷電場的矢量和

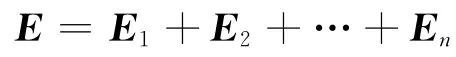
此時，通過該閉合曲面的E通量是

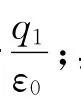
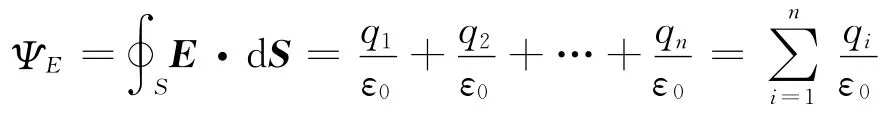
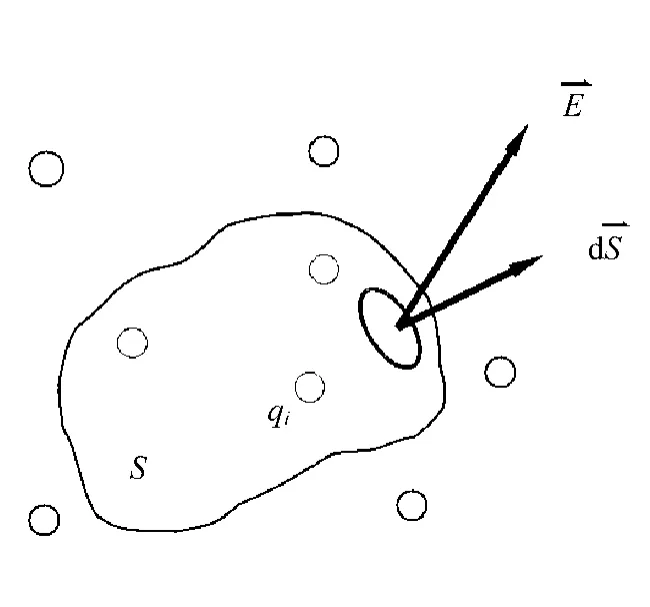
圖4

2.4 正點電荷在球面外

如圖5所示，如果閉合曲面內沒有包圍電荷，電荷在閉合曲面外面，那么進入閉合曲面的電場線等于穿出閉合曲面的電場線，所以總的E通量為0，即

綜合以上討論，不難得出結論，在靜電場中，通過任一閉合曲面的E通量，等于該曲面內電荷量的代數和除以ε0，一般寫為

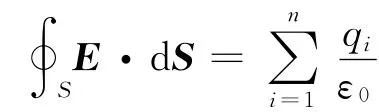
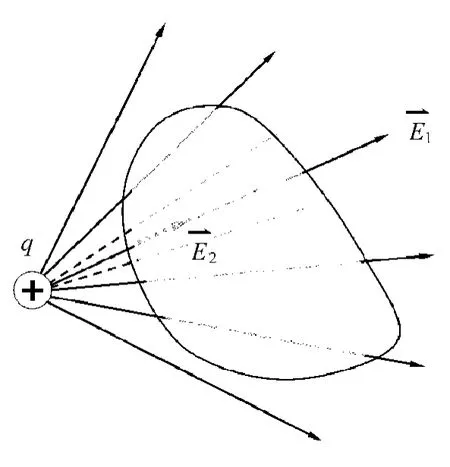
圖5

3 對高斯定理的理解［5－7］

1）在等式左邊的積分中，E是曲面S上各處的電場強度。閉合曲面即為高斯面。選取高斯面時，一般是根據對稱性，使曲面的法線平行于該處的E，或使法線垂直于該處的E。

3）高斯面內以及面外的電荷位置的改變對高斯面上的通量沒影響，但對高斯面上的電場強度是有影響的。

4）在實際應用中，高斯定理常用于電荷具有某種對稱分布時所激發的對稱的電場分布，即軸對稱、球對稱、面對稱。

［1］高本領.高斯定理的簡密推導［J］.高校理科研究，2009，34：90.

［2］趙凱華，陳熙謀.電磁學［M］.北京：高等教育出版社，2003.

［3］胡盤新，湯毓駿，鐘季康.普通物理學簡明教程［M］.2版.北京：高等教育出版社，2007.

［4］韋芙芽，張小林，葉愛華.高斯定理的直觀教學［J］.電氣電子教學學報，2009，31（2）：42－44.

［5］王先菊.高斯定理教學探討［J］.考試，2010，18：182.

［6］沈晴，顧學文，徐筠，等.關于推證高斯定理不同方法的討論［J］.物理通報，2011，40（9）：18－20.

［7］張清澤，陶宗明，陳宇.對高斯定理特性與應用的認識［J］.高等函授學報，2011，24（1）：29－30.

［8］付靜，姜廣軍，袁明霞.普通物理學中磁場安培環路定理的證明［J］.長春工業大學學報：自然科學版，2012，33（6）：709－710.