考慮監測噪聲的陀螺儀剩余壽命在線預測

馮 磊， 王宏力， 韓曉霞， 周志杰

0 引 言

陀螺儀是慣性導航系統的敏感部件，其性能的優劣直接決定整個系統的導航精度［1］。隨著使用時間的增長，陀螺儀性能不可避免地發生退化。在這種情況下，及時有效地預測陀螺儀的剩余壽命，適時采取必要的維護手段，對于提高整個慣性導航系統的可靠性與安全性有著至關重要的作用［2］。

現有的預測方法中，一般假設設備的性能退化變量直接可觀測，并且可以完整地反映設備的退化狀態。通過建模設備的退化過程，預測退化狀態達到給定失效閾值的時間，進而預測設備的剩余壽命［3］。但是，工程實際中，直接測量的退化變量因受到各種噪聲與誤差的影響，不能精確反映設備的退化狀態，這種測量被稱為不完整測量［4］。例如，在測試慣性導航系統的陀螺儀漂移系數過程中，由于受到各種因素的影響，測量結果不可避免地存在噪聲干擾與誤差。為解決直接監測量帶噪聲的問題，可以采用狀態空間模型，建模設備實際的退化過程以及退化過程與不完整測量之間的關系，通過濾波技術預測設備的剩余壽命。此外，根據濾波算法的預測方程與更新方程可以方便地實現在線預測。因此，基于狀態空間模型的剩余壽命預測方法日益受到研究人員的重視。但是，現有研究中大都直接利用退化狀態的估計均值作為設備實際的退化狀態值，不能精確反映狀態估計的不確定性對后續剩余壽命預測的影響［5-7］。

基于上述分析，文中考慮直接監測量含有噪聲的剩余壽命預測問題，利用基于線性漂移的布朗運動建模陀螺儀退化過程，然后構建狀態空間模型表征不完整測量與實際退化狀態的關系。在利用期望最大化算法與卡爾曼濾波聯合估計與更新未知參數與退化狀態后，充分考慮狀態估計的不確定性，將估計的退化狀態分布引入剩余壽命預測過程中，得到剩余壽命概率密度函數的參數化解析形式。一旦新的監測值可用，即可更新未知參數與退化狀態。相應地，可以更新剩余壽命的分布，最終實現在線剩余壽命預測。實驗結果表明了所提方法具有較小的預測不確定性。

1 基于狀態空間技術的剩余壽命預測

1.1 退化過程建模

假設設備實際的退化過程｛X（t），t≥0｝可由基于線性漂移的布朗運動建模，即X（t）可表示為

基于線性漂移的布朗運動被廣泛用于退化過程建模，其最大優點是可以根據首達時間（First Hitting Time，FHT）的概念定義設備的壽命，進而得到壽命分布的解析形式，即逆高斯分布［8］。因此，時刻ti設備的剩余壽命可以定義為退化過程｛X（t），t≥ti｝達到預先設定的失效閾值的首達時間［9］，即剩余壽命Tr可定義為

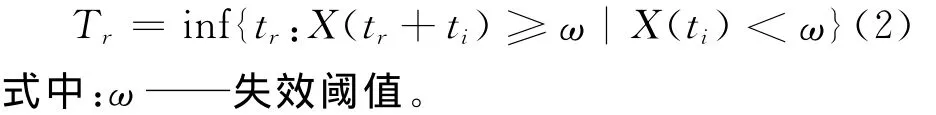
若直接監測的退化變量不含有噪聲，則可根據式（2）直接得到剩余壽命分布的概率密度函數。但是，正如上節所述，不完整測量廣泛存在于工程實際中，直接監測信息不能精確反映設備的退化狀態，因此，不能直接利用式（2）計算設備剩余壽命。文中利用狀態空間技術解決此問題。

1.2 狀態空間模型的構建

為建模直接監測與實際退化之間的關系，采用如下加性噪聲模型構建觀測方程:

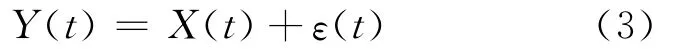
其中，ε（t）為噪聲項，假設ε（t）～N（0，σ2）且與B（t）相互獨立。

為了辨識實際的退化狀態，首先將動態系統（1）和（3）離散化，得到離散時間點tk＝kΔt，k＝1，2，…的狀態方程和觀測方程:

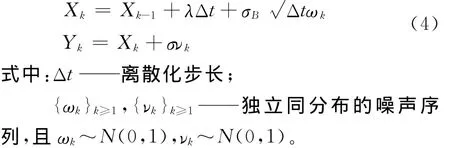
根據狀態空間模型（4），應用卡爾曼濾波［10］估計當前時刻實際的退化狀態。首先定義E（Xi｜Y1∶i）和＝Var（Xi｜Y1∶i）為利用當前時刻的整個觀測序列Y1∶i＝Δ｛Y1，Y2，…，Yi｝得到的狀態Xi的條件期望與方差，即Xi～N（X∧i｜i，Pi｜i）。現有研究大都直接將狀態估計的均值作為其實際值，直接可以得到時刻ti，剩余壽命概率密度函數為:

式（5）沒有考慮狀態估計的不確定性，為了減少剩余壽命預測的不確定性，文中將估計的狀態分布引入后續的剩余壽命預測中。根據全概率定律，可以得到當前時刻ti，剩余壽命概率密度函數為:

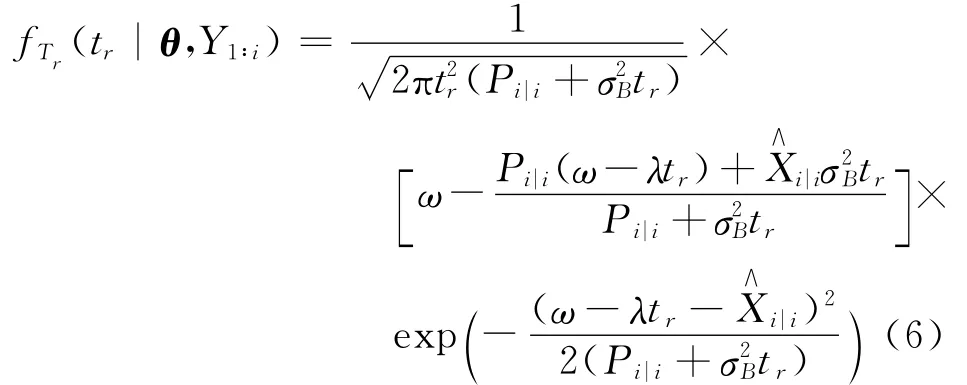
2 參數估計算法

由于模型中含有未知參數，并且狀態是未知的，因此，采用EM算法解決存在未知狀態時的參數極大似然估計問題。為后續表示方便，首先定義當前時刻的狀態序列為Xi｝。通過迭代計算且最大化包含完整數據集（X1∶i，Y1∶i）的對數似然函數的條件期望，EM 算法能夠產生一個估計序列收斂到參數的極大似然估計值［11］。令θ∧（j）表示 EM 算法第j次迭代所得的估計值，則完整數據對數似然函數的條件期望可表示為:

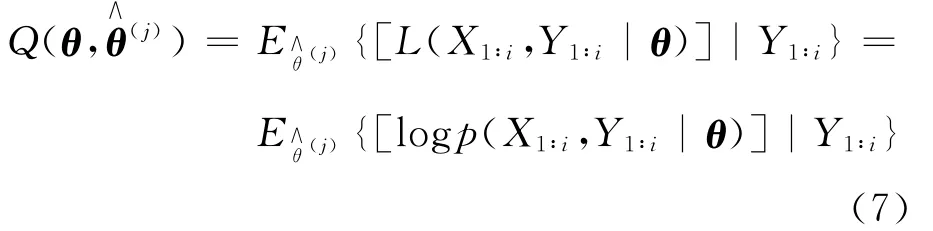
其中，L（X1∶i，Y1∶i｜θ）＝logp（X1∶i，Y1∶i｜θ）為完整數據對數似然函數。總結起來，參數估計程序包含如下兩個步驟:

1）E 步。

計算 Q（θ，θ∧（j））。

2）M 步。

求解:

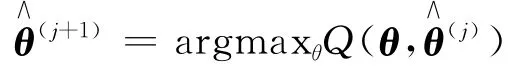
具體到文中構建的狀態空間模型（4），為了計算對數似然函數的條件期望，對于k＝1，2，…，i，首先定義如下變量:

經過一系列代數運算，可以得到

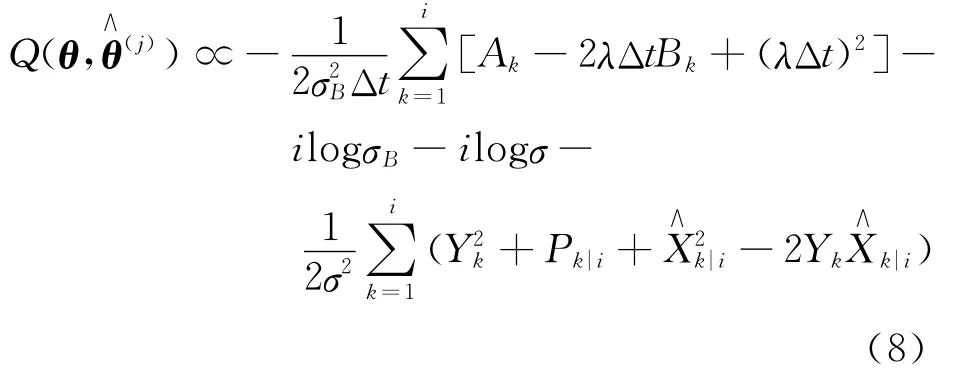
其中

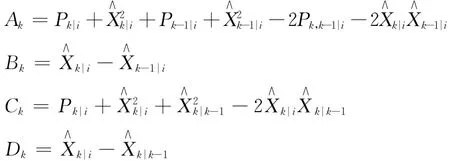
為降低參數空間的維數，減少計算復雜度，分別計算式（8）相對于參數λ，σB和σ的偏導數，并且令這3個偏導數為零，可得

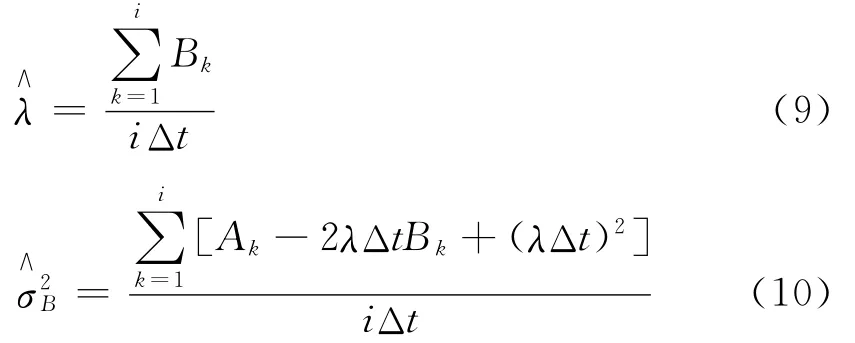
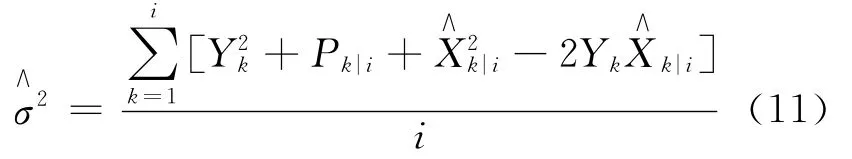
根據一階必要條件可知，最優的參數估計值必滿足式（9）～式（11）。因此，可通過直接計算得到未知參數的估計值。

由上述推導可知，一旦獲取新的觀測值，就可以利用卡爾曼濾波和EM算法，估計和更新退化狀態及未知參數。相應地，根據式（6）可以更新剩余壽命的概率分布，實現實時剩余壽命預測。

3 陀螺儀剩余壽命預測實驗

3.1 問題描述

陀螺儀漂移是表征其性能的一項重要指標［12］。運行狀態下，陀螺儀的轉子高速旋轉必然造成轉軸的磨損，引起漂移系數的增長，當漂移系數增大到預先設定的閾值，即認為系統發生失效。本實驗選取敏感軸方向的一次項漂移系數作為衡量陀螺儀退化狀態的性能指標。該系數的值一旦達到失效閾值0.38°／h，即表明陀螺儀已經失效。對陀螺儀連續工作測試，采樣間隔為3h，所得到的測試數據共96組，如圖1所示。

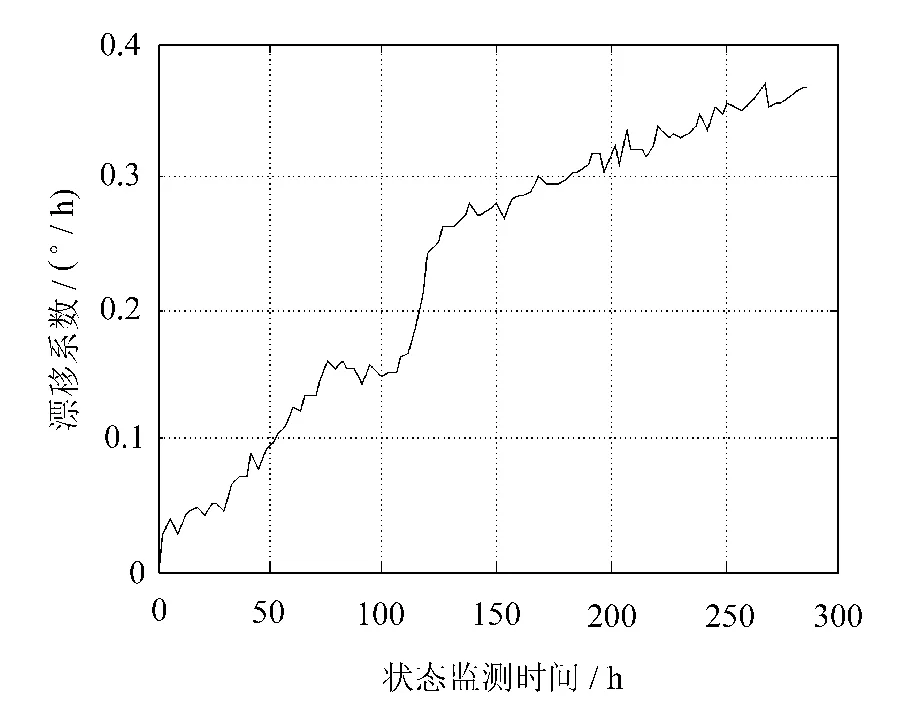
圖1 漂移系數測試數據

3.2 實驗結果

為預測陀螺儀的剩余壽命，首先利用EM算法對參數進行估計與更新。各未知參數的估計與更新結果如圖2所示。

由圖2可知，隨著監測數據的增加，各未知參數很快收斂到各自的穩定值，說明所提參數估計方法的有效性。其中，參數a最終的估計結果為0.004 6，σB的估計結果為0.007 8，σ的估計結果為0.004 5。

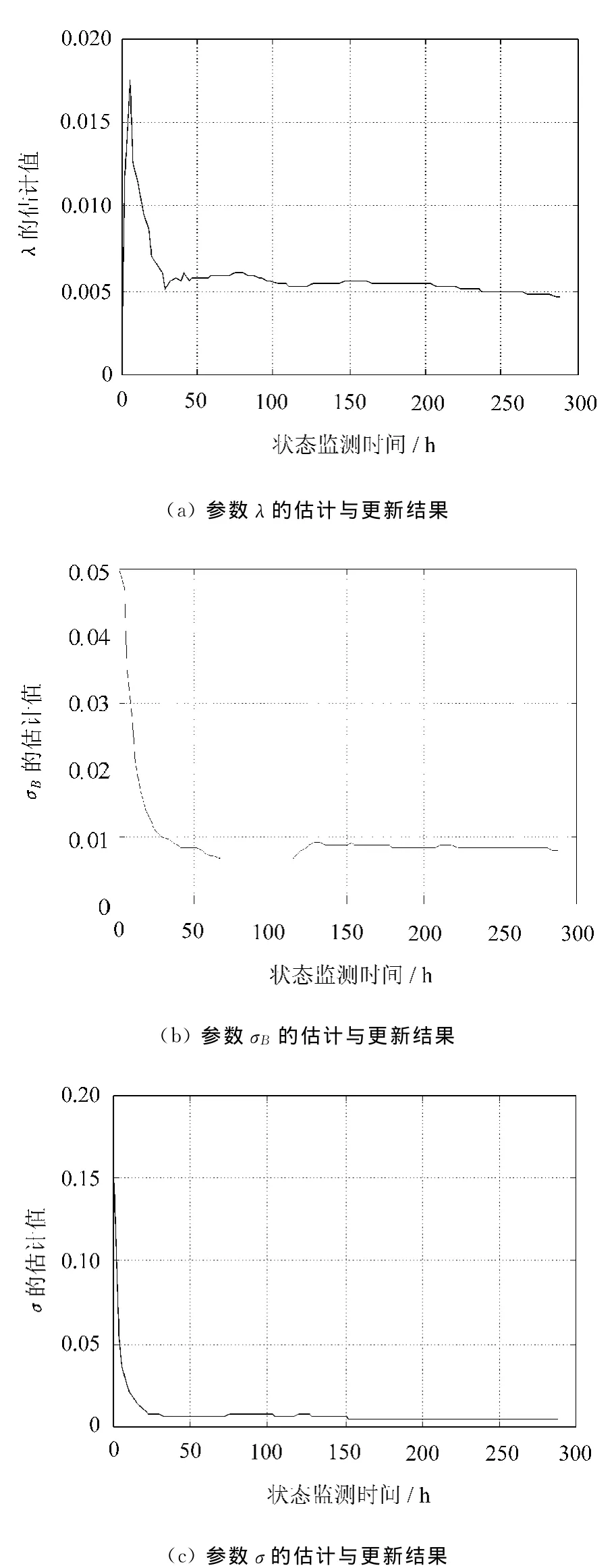
圖2 參數估計與更新結果

為了驗證文中方法的有效性，將文中模型與不考慮狀態估計不確定性的模型做比較研究。為表示方便，將文中所構建的模型稱為模型1，不考慮狀態估計不確定性的模型為模型2。以第90個到96個數據為例，剩余壽命預測結果如圖3所示。

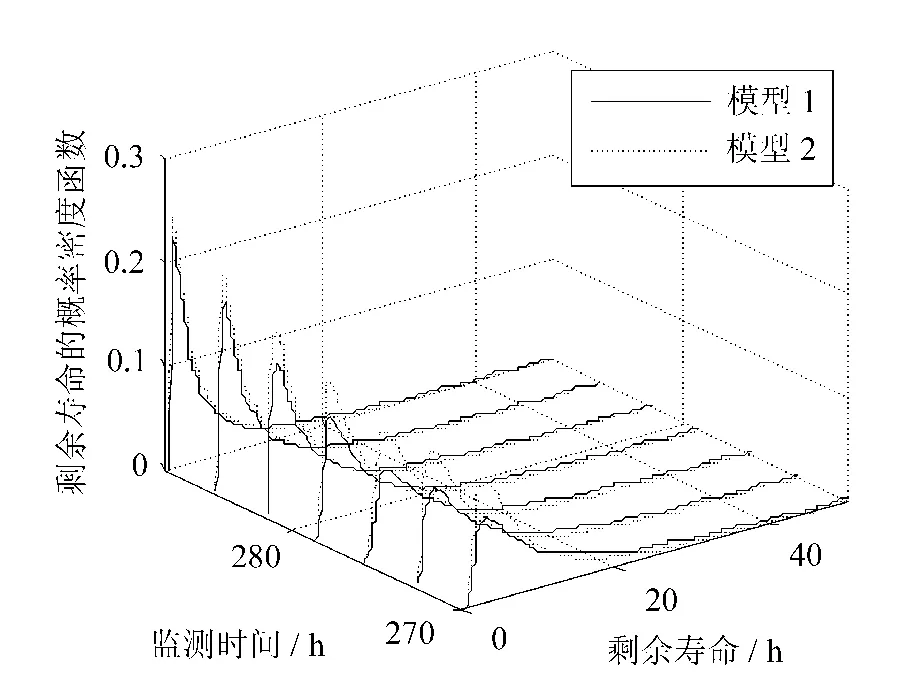
圖3 兩種模型的剩余壽命預測結果的比較

由圖3可知，兩種模型的預測曲線都比較平滑，但是文中模型考慮了退化狀態估計的不確定性，因此，利用文中方法預測得到的剩余壽命的概率密度曲線更加緊致，預測結果的不確定性小。由于后續的維護策略優化需要預測的剩余壽命信息，因此，文中方法可以減少維護策略建模的不確定性，降低失效風險，提高維護效率。

4 結 語

陀螺儀剩余壽命預測實踐中，受各種因素的影響，直接監測的退化變量含有噪聲，不能準確反映陀螺儀的退化狀態。為解決此問題，構建了狀態空間模型建模實際退化過程以及直接監測與退化狀態間的關系，并且考慮狀態估計的不確定性，將其引入剩余壽命預測過程，最終實現剩余壽命的在線預測。仿真實驗表明，文中所提方法能夠較好地解決陀螺儀剩余壽命預測的相關問題，并且可以減少預測的不確定性，為后續的維護策略安排提供準確而實時的預測信息。

［1］ 胡昌華，馬清亮，鄭建飛.導彈測試與發射控制技術［M］.北京:國防工業出版社，2010.

［2］ Zhou Z J，Hu C H，Xu D L，et al.A model for re-al-time failure prognosis based on hidden Markov model and belief rule base［J］.European Journal of Operational Research，2010，207（1）:269-283.

［3］ Si X S，Wang W，Hu C H，et al.Remaining useful life estimation:A review on the statistical data driven approaches［J］.European Journal of Operational Research，2011，213（1）:1-14.

［4］ Sun J Z，Zuo H F，Pecht M G.Advances in sequential monte carlo methods for joint state and parameter estimation applied to prognostics ［C］／／Prognostics and System Health Management Conference.Shenzhen，China:［s.n.］，2011:1-7.

［5］ Christer A H，Wang W，Sharp J M.A state space condition monitoring model for furnace erosion prediction and replacement ［J］.European Journal of Operational Research，1997，101（1）:1-14.

［6］ Carr M J，Wang W.Modeling failure modes for residual life prediction using stochastic filtering theory［J］.IEEE Transactions on Reliability，2010，59（2）:90-96.

［7］ Wang W，Carr M J，Xu W，et al.A model for residual life prediction based on Brownian motion with an adaptive drift［J］.Microelectronics Reliability，2011，51（2）:285-293.

［8］ Chhikara R S，Folks J L.The inverse gaussian distribution as a lifetime model［J］.Technometrics，1977，19（4）:461-468.

［9］ Lee M L T，Whitmore G A.Threshold regression for survival analysis:Modeling event times by a stochastic process reaching a boundary［J］.Statistical Science，2006，21（4）:501-513.

［10］ 王志賢.最優狀態估計與系統辨識［M］.西安:西北工業大學出版社，2004.

［11］ Schon T B，Wills A，Ninness B.System identification of nonlinear state-space models ［J］.Automatica，2011，47（1）:39-49.

［12］ 姜楠，張雙才，蘇莉蔚.基于 MEMS的慣性測量系統［J］.長春工業大學學報:自然科學版，2010，31（2）:181-184.