斜交角度對預應力混凝土空心板梁受力特性的影響
李金龍,賈艷敏,閔兆興
(東北林業(yè)大學土木工程學院,黑龍江哈爾濱 150040)
高速公路的大力建設是為了適應全國經(jīng)濟的快速發(fā)展,加快區(qū)域之間的溝通與交流。為了滿足選線的需要,斜交跨越的方案往往更加合理。空心板梁由于構造簡單,施工方便,建筑高度小,因而在斜交方案中使用較多。但是預應力混凝土斜交空心板的受力特性比較復雜,它不僅具有斜交橋的特點,同時也因為其挖空率較大,壁厚較小,又具有薄壁結構的特性,這使得預應力混凝土斜交空心板橋的設計十分不便[1-3]。本文通過有限元分析軟件對不同斜度的預應力混凝土空心板梁進行計算、分析,得出斜度對預應力混凝土空心板梁受力特性的影響,為工程設計提供參考。
1 現(xiàn)場試驗
本文以某高速公路預制梁場單梁靜載試驗為依托,對該梁場所生產(chǎn)的斜度45°、跨徑20m的預應力混凝土空心板梁進行靜載試驗(截面尺寸如圖1所示)。試驗采用鋼絞線進行三級加載,在跨中和端點以磁力表架為支撐,用百分表設置撓度測點。在跨中截面沿梁高方向布置混凝土應變片,用BZ2205C型應變測試儀測量加載時混凝土所產(chǎn)生的微應變,現(xiàn)場測點如圖2、圖3所示。每級加載后待梁體穩(wěn)定后記錄試驗讀數(shù),得到荷載對梁體跨中截面應力以及撓度產(chǎn)生的影響。現(xiàn)場加載情況如圖4所示。
2 斜度對空心板梁受力特性影響分析
2.1 分析模型的建立
通過ABAQUS有限元分析軟件建立相應模型。主梁采用Solid三維實體單元,單元類型為C3D20R。預應力鋼絞線通過Truss單元模擬。用降溫法實現(xiàn)梁體的預應力。

圖1 跨中截面尺寸(單位:mm)
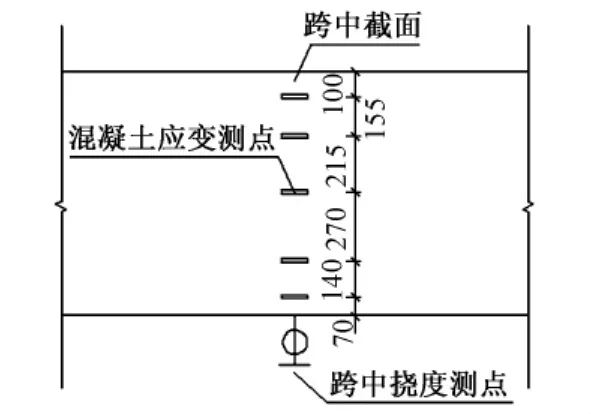
圖2 現(xiàn)場測點布置(單位:mm)

圖3 梁體及測點外觀

圖4 現(xiàn)場加載情況
工程試驗數(shù)據(jù)與ABAQUS有限元分析軟件模擬數(shù)據(jù)對比如表1所示。由表1可見,模型計算所得數(shù)值與現(xiàn)場實際試驗值接近。因此,本模型可以反映實際加載時空心板梁的受力特性。
同樣,用ABAQUS有限元軟件分別模擬交通部《公路橋梁通用圖》跨徑為 20m,斜度為 0°,15°,30°和45°的預應力空心板梁單梁模型(截面尺寸如圖1所示)。按照公路-Ⅰ級的荷載要求,以跨中截面荷載效應相等為原則換算出靜載試驗所需的試驗荷載。在跨中施加集中荷載Pk1=78 kN,Pk2=156 kN,Pk3=234 kN(其中 Pk1,Pk2,Pk3分別為設計荷載的 30%,60%,90%);在彈性范圍內(nèi)分析斜交角度對空心板梁受力特性的影響。

表1 靜載試驗數(shù)據(jù)與ABAQUS有限元軟件計算數(shù)據(jù)對比
2.2 斜度對撓度的影響
撓度作為工程設計中的一項重要設計指標,直觀地反映了截面的彎矩大小[4]。在分析模型中,通過跨中施加Pk1,Pk2,Pk3荷載求得跨中撓度變化如圖5所示。三級加載后的變形云圖如圖6所示。
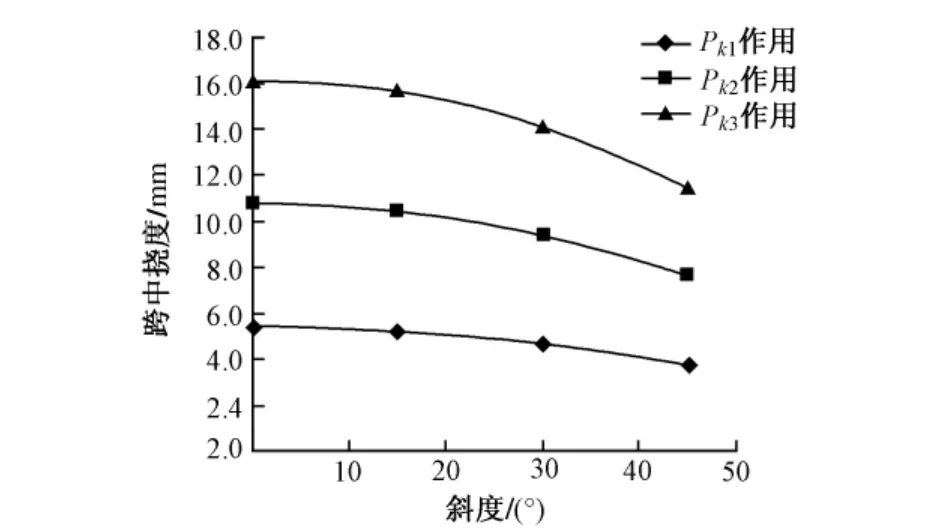
圖5 集中載Pk1,Pk2,Pk3作用下跨中截面撓度隨斜度變化曲線

圖6 斜度30°空心板Pk3作用下的變形(單位:mm)
圖5表明,在跨中集中荷載Pk1,Pk2,Pk3作用下,跨中截面撓度隨斜度的增大而減小。當斜度<15°時,這種變化較小。當斜度>15°時,這種變化隨斜度增大變得更大。斜度15°,30°,45°空心板梁的撓度分別約為0°空心板梁的96.9%,87.3%,71.0%。由于斜度的存在,在跨中集中載的作用下,表現(xiàn)出彎扭耦合效應,即空心板梁產(chǎn)生彎矩的同時伴隨產(chǎn)生相應的耦合扭矩,產(chǎn)生扭矩的同時也會產(chǎn)生相應的彎矩;也就是斜梁的豎向撓曲變形和扭轉(zhuǎn)角之間對應著耦合效應,導致跨中彎矩的折減,進而所反應出的撓度變形減小[5]。
2.3 斜度對跨中截面應力的影響
《公路鋼筋混凝土及預應力混凝土橋涵設計規(guī)范》(JTG D62—2004)中對全預應力構件明確規(guī)定,在荷載作用下,正截面的受拉邊緣不允許出現(xiàn)拉應力。因此對于構件特征截面的應力控制在設計和施工中顯得尤其重要。沿空心板梁高度方向取5個應力點,距梁底高度分別為60mm,292 mm,475mm,658 mm,825mm,分析在跨中集中荷載Pk1,Pk2,Pk3作用下各點的應力變化。如圖7、圖8和圖9所示。
綜合圖7、圖8和圖9可知:在跨中集中力作用下,空心板梁上下緣應力隨斜度增大而減小。斜度15°,30°,45°空心板梁的上緣應力分別約為 0°空心板的 97.6%,92.7% 和 82.0%。斜度 15°,30°,45°空心板梁的下緣應力分別約為0°空心板的98.1%,89.9%和75.4%。

圖7 Pk1作用下各點應力

圖8 Pk2作用下各點應力

2.4 斜度對支點反力的影響
橋梁結構的支點反力是橋梁設計中的重要數(shù)據(jù),它關系到支座的選取以及橋梁下部結構的整體設計。正確地了解斜度對支點反力的影響,在橋梁設計中至關重要。在Pk1,Pk2,Pk3作用下,不同斜度空心板銳角支點和鈍角支點的反力如圖10所示。
圖10表明,由于扭矩的存在,在跨中集中荷載的作用下,梁體會發(fā)生扭轉(zhuǎn)和翹曲變形。隨著斜度增大,銳角支點所承擔的反力逐漸減小,當斜度>10°時,開始出現(xiàn)負反力,并隨斜度增大而呈負增長趨勢。當斜度>30°時,這種增長趨勢開始減慢。在結構設計中需要充分考慮負反力的出現(xiàn),并設置抗拉支座。

圖10 Pk1,Pk2,Pk3作用下支點反力隨斜度的變化
3 結論
通過建立ABAQUS有限元模型,分析跨徑20m空心板梁受集中荷載Pk1,Pk2,Pk3作用時跨中截面撓度、應力以及支點反力的變化情況,通過試驗數(shù)據(jù)對比,得出以下結論:
1)在跨中集中力作用下,跨中截面撓度隨斜度的增大而減小。斜度15°,30°,45°空心板的撓度約為0°空心板的97%,87%,71%左右。
2)在跨中集中力作用下,空心板梁上下緣應力隨斜度的增大而減小。斜度15°,30°,45°空心板梁的上緣應力約為0°空心板的98%,93%,82%左右。斜度15°,30°,45°空心板梁的下緣應力約為 0°空心板的98%,90%,75%左右。
3)當斜度超過10°時,銳角區(qū)開始出現(xiàn)負反力。斜度15°的空心板梁銳角和鈍角支反力的絕對值比約為0.15,斜度30°的空心板梁銳角和鈍角支反力的絕對值比約為0.45,斜度45°的空心板梁銳角和鈍角支反力的絕對值比約為0.55。
[1]劉漢彩.梁格法在斜橋檢測計算中的應用[D].重慶:重慶大學,2008.
[2]張彧,張慧,馬佳錚.斜交角變化對斜交彎梁橋結構內(nèi)力影響的計算分析[J].石家莊鐵道大學學報:自然科學版,2011,6(2):6-10.
[3]邱利銳.混凝土空心板梁底縱向裂縫對結構受力的影響分析[J].鐵道建筑,2009(3):53-55.
[4]姚玲森.橋梁工程[M].北京:人民交通出版社,2009.
[5]徐濤,呂福鋼,萬其柏.斜橋計算分析的發(fā)展[J].遼寧交通科技,2005(7):71-72.

