基于動應變的橋梁動態稱重及其優化算法

王寧波，任偉新，萬華平

(中南大學 土木工程學院，長沙 410075)

車輛荷載作為在役橋梁最重要的活荷載之一，在橋梁的各種荷載組合中占有重要地位。監測橋上移動車輛荷載，明確其分布特點對在役橋梁承載能力評估、橋梁剩余壽命預測、橋梁結構可靠度設計以及運營維護管理等方面都具有重要意義。

對橋梁移動車輛荷載的測定，目前國內采用較多的方法是路面式動態稱重，它通過在進橋路面段行車道路面埋入(壓電式)或頂部安放(彎板式)傳感器系統來檢測車輛軸重、軸距等信息。路面式動態稱重的優點是能適合任意橋梁結構并可長時間采集數據，其主要缺點是只能測定車輪壓在傳感器上幾毫秒短暫時間段內的動壓力，由于不能記錄動荷載完整的周期振動，通常情況下該壓力值與靜態軸重存在偏差［1］，此外，路面式動態稱重的識別精度受傳感器寬度、車輛行駛速度以及路面平整度的影響很大。

基于動應變的橋梁動態稱重是另外一種車輛荷載測定方法，通過在橋梁不同截面底部安裝應變計測定車輛過橋時間段內動應變響應，以此來識別車速、軸距，以及軸重、車重等信息。相較路面式動態稱重而言，基于動應變的橋梁動態稱重對車輛荷載信息測試記錄時間長，能獲取的數據量大，還具有系統安裝維護簡便，不中斷交通、對路面無破壞、耐久性好等優點。Moses等［2］首次提出了根據橋梁動應變進行車輛動態稱重的一般原理，Peters［3］將這一應用延伸至涵洞結構，并引入“峰值法”來進行荷載識別。20世紀末，歐盟委員會應10個參與國相關組織機構的提議啟動WAVE project，針對路面車輛荷載及軸重測定展開一系列理論與試驗研究［4］，至此基于動應變的橋梁動態稱重開始受到關注。Rowley等［5］在荷載識別中采用正則化優化算法，與初始最小二乘法的結果比較并得出結論:采用精確的橋梁影響線結合正則化技術將大幅提高動態稱重精度。Chatterjee［6］將小波變換用于應變信號處理以提取精確的車軸信息。Michael［7］針對車輛行駛在橋面不同橫向位置時產生明顯不同動應變的現象，研究了二維橋梁移動荷載識別問題，并初步考慮多個車輛連續從橋上通過的工況。O’Brien等［8］根據實測橋梁應變數據對影響線進行反算，從而實現了對橋梁影響線測定。基于動應變的橋梁動態稱重因為其數據信息量豐富、安裝維護簡便、耐久性能好等優點在歐、美、日、等國家逐漸受到青睞，一些國家開始以此來取代傳統路面式動態稱重系統［9-10］。

基于動應變的橋梁動態稱重研究多采用理論仿真分析與現場試驗研究相結合的手段。本文結合車-橋耦合振動模型進行仿真分析，詳細闡述了根據動應變進行橋梁動態稱重(包括車輛行駛速度、軸距、軸數的識別以及車輛、車軸稱重)的基本理論，并針對已具備一定精度的橋梁動態稱重初始結果值，采用梯度法進行多參數局部優化研究，進一步提高結果精度，體現了基于動應變的橋梁動態稱重算法的可行性。

1 基于動應變的橋梁動態稱重基本理論

根據車輛從橋上行駛所產生的橋梁動應變來提取車輛荷載，是典型的“第二類反問題”。車輛過橋時橋梁動應變信號按其產生原因主要可分成車輛荷載引起的橋梁振動部分、橋梁自由振動部分和噪聲部分，若忽略橋梁慣性力(即橋梁自由振動部分)，移動車載部分產生的橋梁動應變可近似等同于相應影響線與荷載值的乘積。根據這一特性采用橋梁影響線模擬實測動應變信號，得到應變理論值，比較實測值與理論值，并結合最小二乘法求解車輛各軸重，即實現動態稱重。

1.1 橋梁影響線確定

橋梁影響線描述橋梁在移動單位荷載作用下的靜態特性，橋梁影響線精度是貫穿動態稱重的重要指標。理論上可通過橋梁的尺寸、材料、支撐等參數計算獲取不同斷面橋梁影響線，實際情況下由于支撐條件不確定性(多介于理想簡支與完全固支之間)、材料老化、彈性鋪裝等因素使得該方法的計算結果并不理想，通常需在上述基礎上通過調整支座約束條件對影響線作適當修正。此外，還可以通過利用標準車輛過橋的實測數據直接計算得到橋梁影響線［8］。

1.2 橋梁動態稱重基本理論

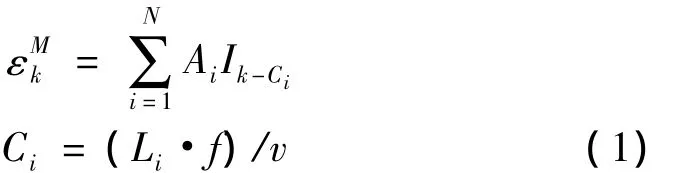
其中:N為車輛軸數;Ai為第i軸軸重;Ik-Ci為測點k對應第I車軸影響線縱坐標值，根據橋梁影響線獲得;Li為第i軸與第1軸之間的距離(L1=0);f為數據采樣頻率;v為車輛行駛速度;Ci為與軸距Li相對應的采樣點數。

定義誤差函數:

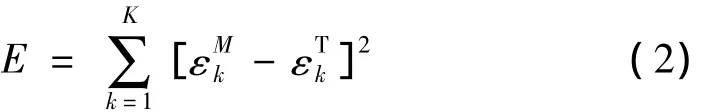
聯立式(1)，式(2)，根據最小二乘原理:

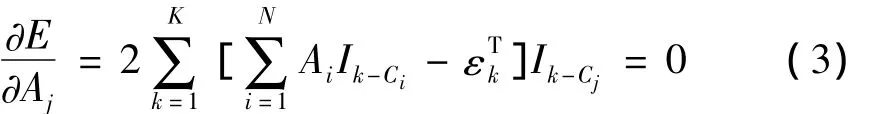
K指采樣點總數;j=1，…，n，表示車軸數。對式(3)化簡得:

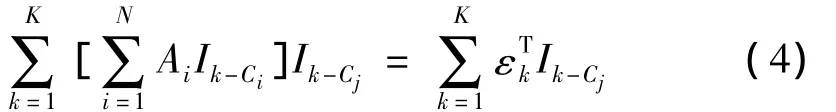
j有N個取值，對應N個等式，令:

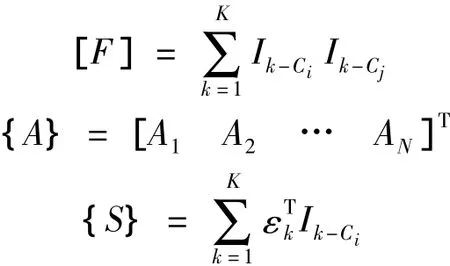
則有:

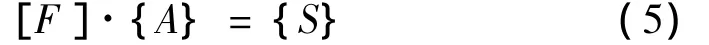
求解方程(5)即得到車輛軸重列陣Aj。從以上推導過程不難發現，采用該方法計算得到的車輛軸重值精度受車輛行駛速度、軸距等參數精度的影響很大。

2 初始識別結果值局部優化

基于動應變的橋梁動態稱重算法，需以準確的車輛行駛速度、軸距、等信息為基礎，當前者識別結果存在誤差時將直接導致軸重識別偏差。針對這一問題，對上述橋梁動態稱重算法得到的初始結果值進行局部優化，以降低速度、軸距等參數識別誤差對軸重的影響，進一步提高精度。

本文選用梯度法作為局部優化算法，對車輛速度、軸距及軸重等識別值進行多參數局部優化，具體優化過程定義如下:

目標函數，最小值:

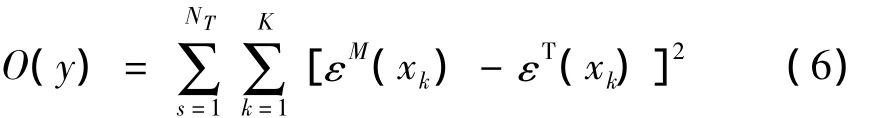
其中:K是總采樣數點，k表示第k采樣點;xk與k相對應，表示第1軸與指定參考點之間的距離;NT表示采用的測點總數。

優化參數:

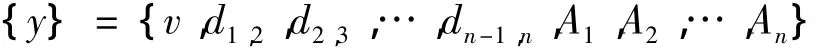
其中:dn-1，n表示第n-1 軸與n軸之間距離，即:dn-1，n=Ln-Ln-1。v，Ai含義與前文相同。

初始值:

選定橋梁動態稱重初始結果值作為優化算法初始輸入值。

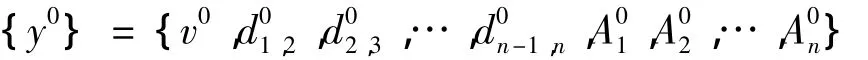
約束條件:

為保證目標函數O(y)最小值的唯一性，即Hessian矩陣特征值均為非負，需對參數取值范圍進行約束，針對優化參數，v，d1，2，d2，3，…，dn-1，n，A1，A2，…，An的具體約束條件為:

(1)速度v取值范圍與初始值v0偏差±5%，這要求速度的初始識別精度±5%在范圍內［7］。

(2)當識別的初始值足夠精確時，無需對軸距值進行約束，本文設定上下限值范圍與初始值偏差±20%。

(3)軸重總和(即車輛總重量)與速度v之間關系如文獻［11］。

(4)所有參數取值均為正。約束條件表達式如下:

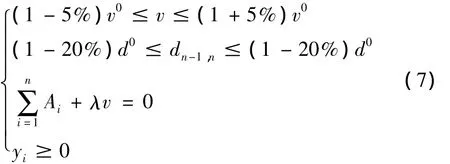
式中:λ=k∫ε(t)，k是與測點對應的橋梁影響線相關的常數。

結合matlab7.0優化工具箱fmincon函數對橋梁動態稱重初始結果值進行優化研究，通過迭代計算求解該有約束優化問題的極小值，從而實現對車輛行駛速度、軸距、軸重等參數的局部優化，進一步提高其精度。基于動應變的橋梁動態稱重及其優化算法基本流程如圖1。

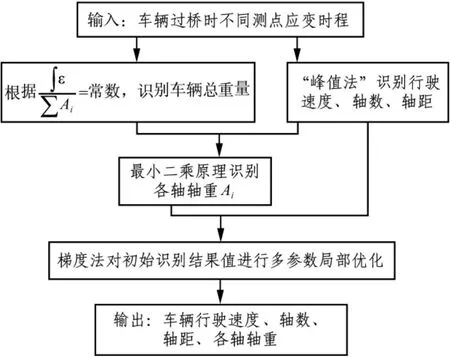
圖1 橋梁動態稱重與優化算法流程Fig.1 Flowchart for bridge WIM and optimization algorithm

3 算例分析

以三軸車輛行駛通過簡支梁橋為例，建立汽車-橋梁耦合振動方程，并進行迭代求解模擬車輛以恒定速度過橋時橋上測點動應變響應，根據模擬的動應變響應曲線對本文基于動應變的橋梁動態稱重算法進行數值仿真。

三軸車輛模型如圖2所示，該模型對應移動荷載識別對象(或優化參數個數)共 6個，分別為v，d1，2，d2，3，A1，A2，A3。車輛模型相關參數源于文獻［12］，具體如下:

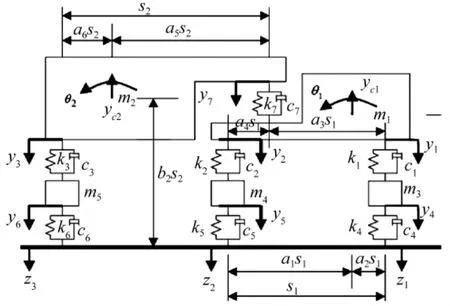
圖2 三軸車輛模型Fig.2 Three-axle vehicle modal

橋梁模型參數:橋長Lb=16 m，抗彎剛度ET=4.36×109Nm2，阻尼系數ξ=0.02，線密度ρA=1.07 ×104kg/m，梁中心線距離底緣0.41 m，假定橋面平順性好，平順性等級設為A級。在橋梁1/8跨、1/4跨和3/4跨截面底緣處設定應變測試點，其中1/8跨測點主要用于車軸檢測，1/4跨和3/4跨測點用于動態稱重研究。

基于以上三軸車輛和橋梁模型，假定車輛在空載和裝載10 t(車輛質心位置不改變)情況下，分別以20、36、54、60 km/h等速度過橋，共記6種工況，模擬計算橋梁1/8、1/4、3/4截面測點動應變響應。首先根據“峰值法”識別車速v、軸距d1，2和d2，3，結合應變曲線積分面積與車輛重量比值恒定的特性識別車輛總重量，采用橋梁應變影響線擬合實測動應變曲線，利用最小二乘法識別三軸重A1、A2、A3。將上述6個參數識別結果值作為局部優化初始值。優化目標函數定義時僅考慮橋梁1/4、3/4截面的兩測點，即(6)式中NT=2，這與實際工況一般選定兩個斷面進行測試相一致。根據本文提出的多參數局部優化算法對移動荷載識別結果進行優化。相關計算及分析結果如表1和圖3所示。

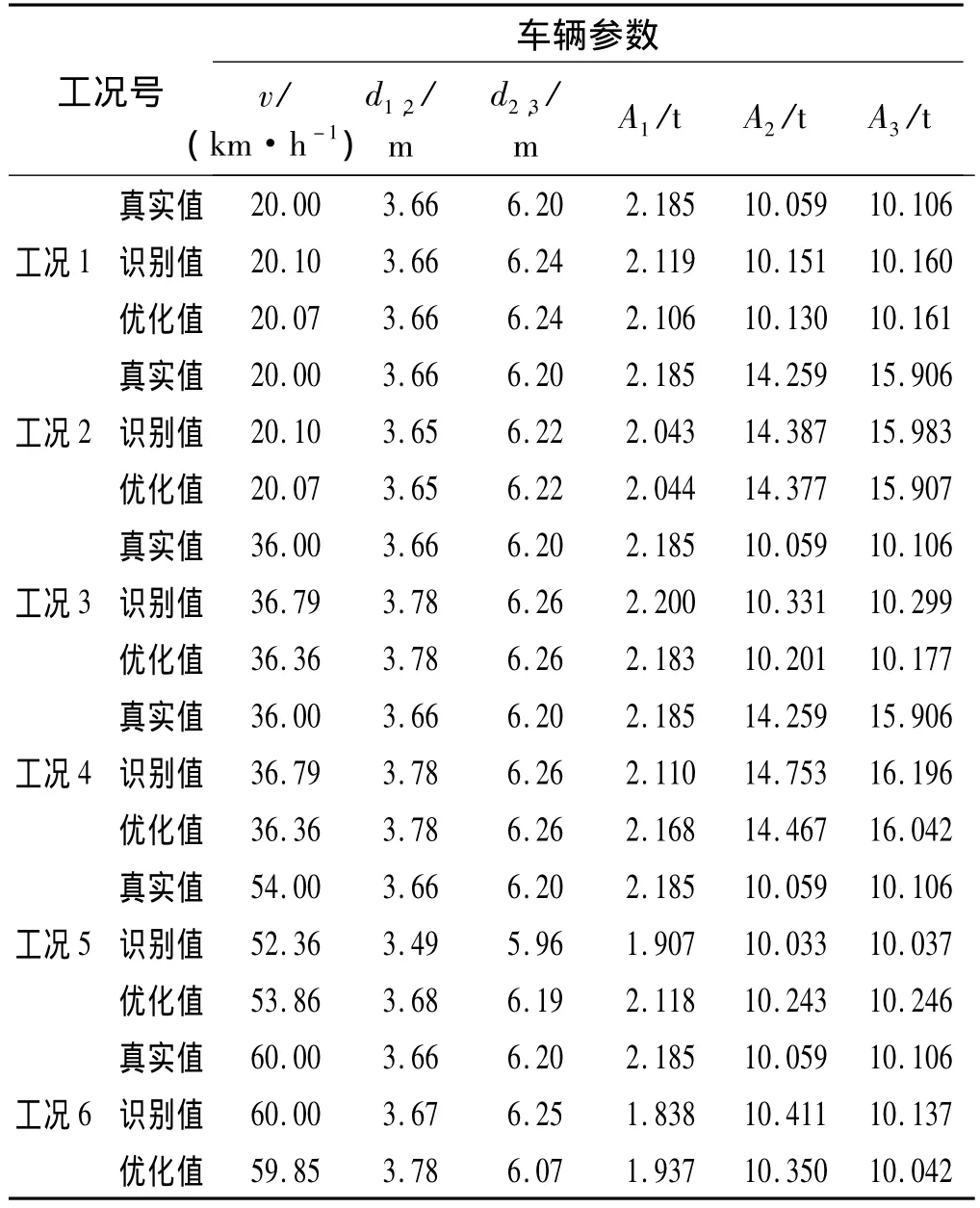
表1 車輛參數識別值及其優化值Tab.1 identification values and its optimization results for vehicle parameters

由表1和圖3的數據比較分析可知，當行駛速度為20 km/h時，初始荷載識別值與優化結果值差異并不明顯，這是因為初始值已具有很高精度;當行駛速度大于36km/h時，優化值較識別結果值更接近真實值，尤其針對車輛行駛速度、軸重等參數，這表明:對橋梁動態稱重初始結果值進行局部優化能夠提高精度。

該數值算例中引用的三軸車輛模型各軸重分布較不均勻，輕軸重量不及總重量1/10，對輕軸識別誤差偏大，圖3(f)最為明顯，此外模型中車輪與路面單點接觸形式過于簡單，不能考慮車輪對路面不平順的包容特性，這導致模擬的橋梁動應變響應曲線與實際情況存在偏差，上述因素的存在使得沒能更好地體現本文橋梁動態稱重及其優化算法在精度方面的優勢。

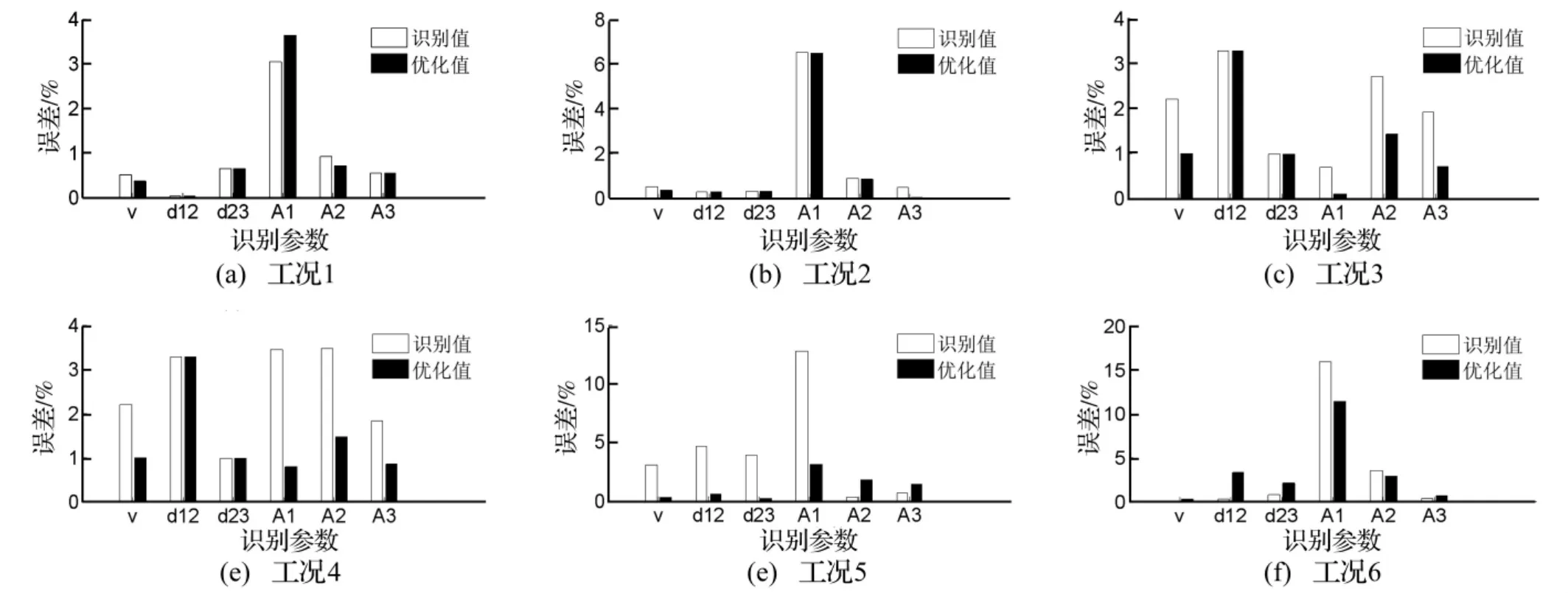
圖3 識別值與優化值誤差比較Fig.3 The error compare of identification values and optimization results

4 結論

根據橋梁動應變響應進行動態稱重，采用梯度法對初始結果值進行多參數局部優化，以消除速度、軸距等識別偏差對整體結果的影響，達到提高車輛荷載識別精度的目的。結合車-橋耦合振動模擬橋梁動應變響應，對上述方法進行數值仿真分析，得到主要結論如下:

(1)基于動應變的橋梁動態稱重對車載信息測試記錄時間長，獲取的數據信息量大，這是準確提取車輛荷載信息的前提條件。

(2)對已經具備一定精度的動態稱重初始結果值進行局部優化，能進一步提高精度，滿足工程應用要求。(3)采用梯度法進行多參數局部優化時，通過合理選定約束條件避免產生多個最小目標值，從而實現快速優化。

(4)橋梁影響線的準確性是影響橋梁動態稱重的重要指標，對影響線的測定是有待進一步研究的問題。

［1］ McNulty P，O'Brien E J.Testing of bridge weigh-in-motion system in sub-arctic climate［J］.Journal of Testing and Evaluation，2003，31(6):1-10.

［2］Moses F.Weigh-in-motion system using instrumented bridges［J］.Transportation Engineering Journal(ASCE)，1979，105(3):233-249.

［3］Peters R J.An Unmanned and Undetectable Highway Speed Vehicle Weighing System［C］//ARRB Transport Research.Proceedings ofthe 13thARRB-5thREAAA Combined Conference(part 6).Australian:Australian Road Research Board，1986:70-83

［4］Jacob B.Action COST 323:Weigh-in-motion of road vehicles［C］//E J O’Brien，et al.Pre-Proceedings of Second European Conference on Weigh-in-motion of road vehicles.Lisbon:European Commission，1999.25-33.

［5］Rowley C，Gonzalez A，O’Brien E J，et al.Comparison of conventional and regularized bridge weigh-in-motion algorithms［C］//B Jacob，et al. Proceedings of the International Conference on Heavy Vehicles.Paris，France:John Wiley，2008.221-230.

［6］ Chatterjee P，OBrien E J，Li Y Y，et al.Wavelet domain analysisforidentification ofvehicle axlesfrom bridge measurements［J］.Computers and Structures，2006，84:1792-1801.

［7］ Michael Q.Bridge weigh-in-motion development of a 2-D multi-vehicle algorithm ［D］.Sweden:Royal Institute of Technology，2003.

［8］ OBrien E J，Quilligan M J，Karoumi R.Calculating an influence line from direct measurements［J］.Proceedings of the Ice-Bridge Engineering，2006，159(1):31-34.

［9］ Kobayashi Y，Miki C，Tanabe A.Long term monitoring of traffic loads by automatic real-time weigh-in-motion［J］.Journal of Structural Mechanics and Earthquake Engineering，2004，69(773):99-111.

［10］ O’Brien E J，Znidaric A，Ojio T.Bridge weigh-in-motion:latest developments and applications worldwide［C］//B Jacob，et al.Proceedings of the International conference on heavy vehicles.Paris，France:John Wiley，2008.25-38.

［11］王寧波，任偉新，李 苗.基于影響線的橋梁移動荷載識別［J］.振動與沖擊，2013，32(3):136-140.

WANG Ning-bo，REN Wei-xin，LI Miao.Moving loads identification of bridge based on influence line［J］.Journal of Vibration and Shock，2013，32(3):136-140.

［12］ Zhu X Q，Law S S.Bridge dynamic responses due to road surface roughness and braking of vehicle［J］.Journal of Sound and Vibration，2005，282:805-830.