模糊聚類(lèi)算法穩(wěn)定圖應(yīng)用于橋梁結(jié)構(gòu)參數(shù)識(shí)別

吳春利 ，劉寒冰 ，王 靜

(1.吉林大學(xué) 交通學(xué)院，長(zhǎng)春 130022;2.吉林建筑工程學(xué)院，長(zhǎng)春 130118)

從橋梁結(jié)構(gòu)上直接監(jiān)測(cè)獲得的位移、應(yīng)變及加速度并不能直接應(yīng)用于結(jié)構(gòu)損傷識(shí)別及狀態(tài)評(píng)估，需要對(duì)決定結(jié)構(gòu)動(dòng)力特性的主要參數(shù)(頻率、振型和阻尼)進(jìn)行識(shí)別。隨機(jī)子空間方法是一種有效的廣受大家青睞的模態(tài)參數(shù)識(shí)別方法［1-2］。但在隨機(jī)子空間識(shí)別結(jié)構(gòu)模態(tài)參數(shù)的方法中，確定合理的系統(tǒng)階次非常重要。選取的系統(tǒng)階次過(guò)少，易遺漏關(guān)鍵模態(tài);反之則易產(chǎn)生虛假模態(tài)，因此找到一種方法來(lái)確定合理的系統(tǒng)階次，進(jìn)而能夠準(zhǔn)確地識(shí)別出結(jié)構(gòu)的動(dòng)力參數(shù)是應(yīng)用隨機(jī)子空間法進(jìn)行模態(tài)參數(shù)識(shí)別的關(guān)鍵。穩(wěn)定圖法由此而生，它是目前常用來(lái)確定系統(tǒng)階次從而識(shí)別模態(tài)參數(shù)最有效的方法。而傳統(tǒng)的穩(wěn)定圖進(jìn)行結(jié)構(gòu)參數(shù)識(shí)別需要人的主觀判斷，不能達(dá)到自動(dòng)識(shí)別的目的。針對(duì)于這一缺陷，本文提出了應(yīng)用模糊聚類(lèi)算法繪制穩(wěn)定圖結(jié)合隨機(jī)子空間法進(jìn)行自動(dòng)識(shí)別結(jié)構(gòu)模態(tài)參數(shù)的方法。

1 隨機(jī)子空間法

協(xié)方差驅(qū)動(dòng)的隨機(jī)子空間識(shí)別方法(Covariancedriven Stochastic Subspace Identification)是基于隨機(jī)狀態(tài)空間模型的性質(zhì)，通過(guò)對(duì)輸出協(xié)方差矩陣進(jìn)行奇異值分解獲得系統(tǒng)矩陣，從而識(shí)別系統(tǒng)的模態(tài)參數(shù)［3-5］。該方法克服了頻域方法的不足，不需要FFT變換，避免數(shù)據(jù)變換引起的截?cái)嗾`差，識(shí)別精度高，其基本識(shí)別過(guò)程如圖1所示。

圖1 協(xié)方差驅(qū)動(dòng)隨機(jī)子空間法流程圖Fig.1 Flow diagram of covariance-driven stochastic subspace identification

2 模糊聚類(lèi)算法

模糊聚類(lèi)算法是基于模糊數(shù)學(xué)的方法，根據(jù)客觀事物之間的特征、親疏程度及相似性，通過(guò)建立模糊相似關(guān)系對(duì)客觀事物進(jìn)行分類(lèi)的一門(mén)技術(shù)，其內(nèi)容涉及統(tǒng)計(jì)學(xué)、生物學(xué)及機(jī)器學(xué)習(xí)等研究領(lǐng)域，在模式識(shí)別、數(shù)據(jù)分析和挖掘以及圖像處理等領(lǐng)域得到了廣泛的應(yīng)用。

在模糊聚類(lèi)算法中，最著名和最常用的劃分聚類(lèi)方法是C-均值及其推廣模糊C-均值(Fuzzy C-Means，簡(jiǎn)稱(chēng)為FCM)算法。FCM算法最早是由J.MacQueen提出，由J.C.Bezdek從硬C-均值算法(HCM)推廣而來(lái)，現(xiàn)已成為最常用和討論較多的聚類(lèi)算法之一［6］。其原理是:首先定義一個(gè)準(zhǔn)則函數(shù)即目標(biāo)函數(shù)，隨機(jī)選擇c個(gè)初始聚類(lèi)中心，然后根據(jù)樣本到聚類(lèi)中心的距離，劃分該樣本到該類(lèi)中;最后再重新計(jì)算每個(gè)類(lèi)的聚類(lèi)中心。上述過(guò)程不斷重復(fù)，直到準(zhǔn)則函數(shù)達(dá)到最小。其描述如下:

令X={xi，i=1，2，…，n}是一訓(xùn)練樣本集，X∈Rp，c為預(yù)定的分類(lèi)數(shù)量，vi(i=1，2，…，c)是第i個(gè)聚類(lèi)的中心，uik(i=1，2，…，c;k=1，2，…，n)為第k個(gè)樣本對(duì)第i類(lèi)的隸屬度函數(shù)，構(gòu)成的隸屬度矩陣U受到以下條件限制:

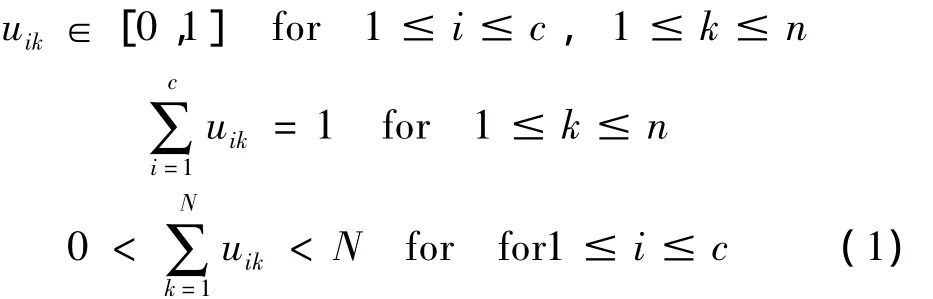
FCM是一種有目標(biāo)的模糊聚類(lèi)算法，其目標(biāo)函數(shù)為:

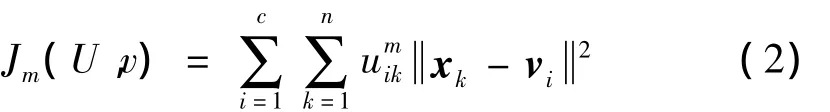
式中，v=(v1，v2，…，vc)，m＞1為模糊參數(shù)，該參數(shù)決定了聚類(lèi)的模糊度，也就是數(shù)據(jù)點(diǎn)可以成為多個(gè)類(lèi)的程度，大多數(shù)情況下m=2。當(dāng)式(2)取到最小值時(shí)結(jié)果最優(yōu)。在式(1)的約束下優(yōu)化(2)可得:

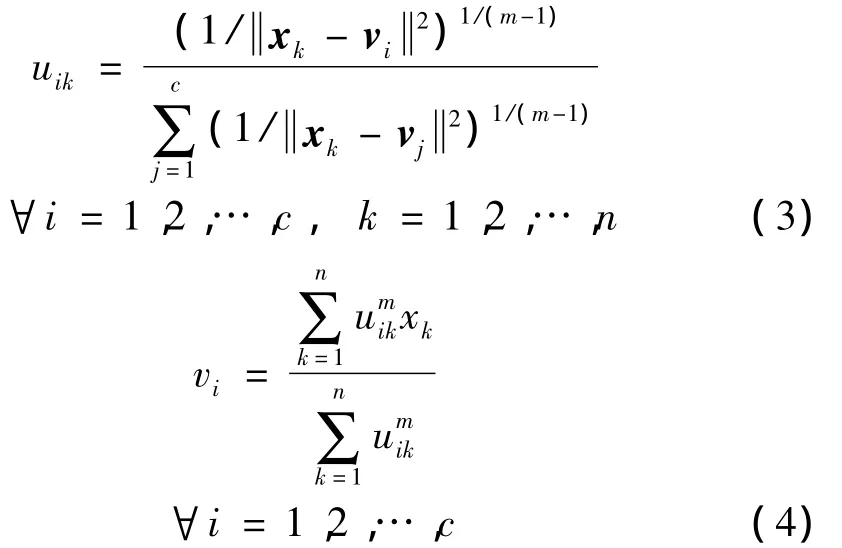
FCM 算法的詳細(xì)步驟如下:

步驟1 初始化:選擇分類(lèi)數(shù)量c、程序終止標(biāo)準(zhǔn)ε＞0以及最大迭代次數(shù)T，初始化隸屬度矩陣U(0)，使其滿(mǎn)足式(1)。令當(dāng)前迭代數(shù)t=1。

步驟2 應(yīng)用式(4)更新聚類(lèi)中心v(t):

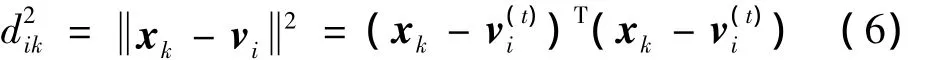
步驟4 由式(3)更新隸屬度矩陣U(t):

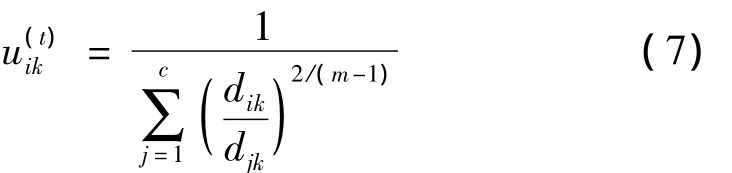
步驟5 終止程序:令t=t+1，重復(fù)步驟2，3和4步，直到滿(mǎn)足U(t)-U(t-1)或者t＞T。

3 基于模糊聚類(lèi)算法的穩(wěn)定圖

傳統(tǒng)穩(wěn)定圖用于識(shí)別系統(tǒng)模態(tài)參數(shù)需要人的主觀判斷，需通過(guò)有經(jīng)驗(yàn)的研究人員對(duì)極軸進(jìn)行取舍。由于人的主觀參與，容易產(chǎn)生誤差，這是用傳統(tǒng)穩(wěn)定圖來(lái)識(shí)別模態(tài)參數(shù)的最大缺陷［7］。因此，人們采用許多方法對(duì)傳統(tǒng)的穩(wěn)定圖進(jìn)行改進(jìn)，使改進(jìn)的穩(wěn)定圖更客觀更智能，在眾多的方法中，基于模糊聚類(lèi)的穩(wěn)定圖算法是被大家廣泛采用且行之有效的方法。目前為止，基于模糊聚類(lèi)的穩(wěn)定圖均是將數(shù)據(jù)繪制在以頻率為橫坐標(biāo)以阻尼為縱坐標(biāo)的二維圖中，每一類(lèi)數(shù)據(jù)點(diǎn)代表了某一階模態(tài)的極點(diǎn)估計(jì)［8］。

在實(shí)際工程中，相對(duì)于頻率及振型兩個(gè)模態(tài)參數(shù)，阻尼受各種因素的影響存在不穩(wěn)定性，本文在基于模糊聚類(lèi)算法的穩(wěn)定圖繪制中以頻率為橫坐標(biāo)以MAC中的任一位置數(shù)據(jù)為縱坐標(biāo)，使模糊聚類(lèi)穩(wěn)定圖的每個(gè)極點(diǎn)包含兩個(gè)信息:頻率f、模態(tài)保證準(zhǔn)則(MAC)，選取這兩個(gè)參數(shù)作為聚類(lèi)因子其限定值可按式(8)進(jìn)行取值。利用模糊聚類(lèi)算法對(duì)穩(wěn)定圖中數(shù)據(jù)進(jìn)行分類(lèi)，找到圖中各分類(lèi)的聚類(lèi)中心，并找到與聚類(lèi)中心最近的數(shù)據(jù)點(diǎn)，這些數(shù)據(jù)點(diǎn)所對(duì)應(yīng)的頻率及振型即為識(shí)別模態(tài)參數(shù)。

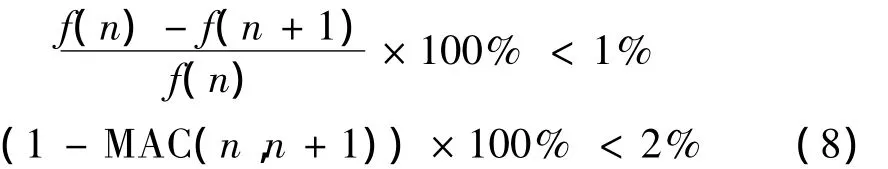
式中，f為計(jì)算頻率，n為模型的階數(shù)，MAC為模態(tài)保證準(zhǔn)則(Modal Assurance Criterion):

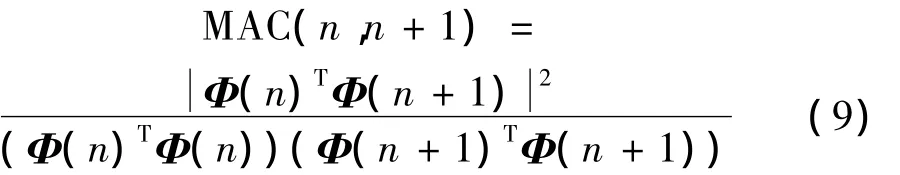
式中，Φ為模態(tài)振型，MAC值在0和1之間，表示模態(tài)振型的相關(guān)性。當(dāng)MAC值等于1時(shí)，表示模態(tài)向量之間是分不開(kāi)的，即表示相鄰不同系統(tǒng)階數(shù)所識(shí)別的模態(tài)振型一致。當(dāng)采集MAC等于0，表示模態(tài)向量之間是相互正交的，在參數(shù)識(shí)別中即表示相鄰不同系統(tǒng)階數(shù)所識(shí)別的模態(tài)振型完全不同。

4 算例

4.1 簡(jiǎn)支梁

為驗(yàn)證隨機(jī)子空間法、模糊聚類(lèi)算法在橋梁結(jié)構(gòu)模態(tài)參數(shù)識(shí)別中的可行性與適用性，采用一等截面簡(jiǎn)支梁作為算例，有限元模型如圖2所示。梁全長(zhǎng)L=40.0 m，截面面積A=8.215 6 m2，截面高H=2.6 m，截面慣性矩Iz=7.673 6 m4，材料密度 ρ=2 500 kg/m3，彈性模量E=30 GPa。結(jié)構(gòu)被均勻劃分為10個(gè)單元，11個(gè)節(jié)點(diǎn)，在11個(gè)節(jié)點(diǎn)處布置應(yīng)變傳感器。

為避免在模態(tài)節(jié)點(diǎn)處激勵(lì)導(dǎo)致無(wú)法識(shí)別相應(yīng)的模態(tài)參數(shù)，在節(jié)點(diǎn)3和節(jié)點(diǎn)11均加入時(shí)長(zhǎng)為3.071 s的白噪聲激勵(lì)來(lái)模擬現(xiàn)場(chǎng)環(huán)境激勵(lì)(如圖2立面圖中黑色箭頭所示)。選取采樣頻率1 000 Hz，11個(gè)節(jié)點(diǎn)共可提出3 071×11=33 781個(gè)應(yīng)變值。由于在實(shí)際工程中存在各種噪聲干擾，因此采用式S=S(1±λsrand(0，1)，對(duì)測(cè)量得到的應(yīng)變值加入噪聲，式中S為測(cè)量應(yīng)變值，rand(0，1)是均值為零，方差為1的高斯分布隨機(jī)數(shù)，λs為測(cè)量信號(hào)的噪聲水平。在該簡(jiǎn)支梁中考慮分別加入λs=1%、λs=5%和λs=10%三種噪聲情況。

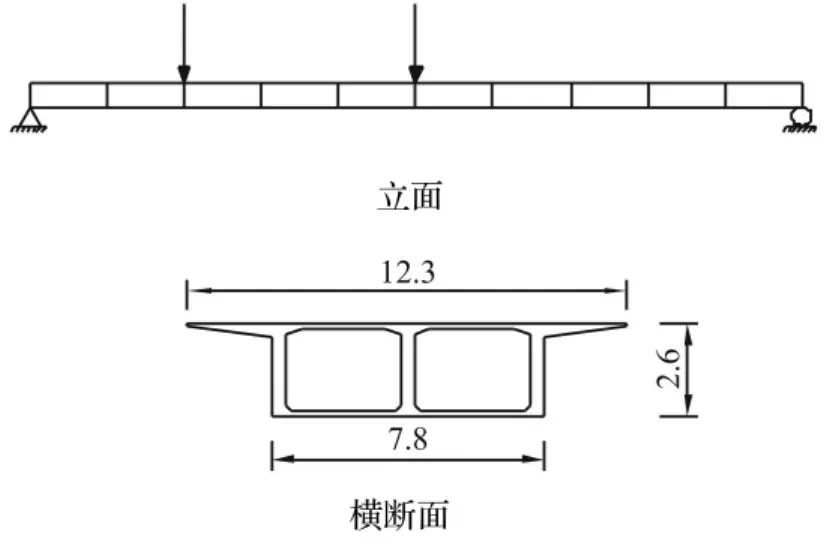
圖2 簡(jiǎn)支梁有限元模型Fig.2 Finite element model of the simple beam

將考慮了噪干擾的應(yīng)變時(shí)程值作為輸入數(shù)據(jù)，系統(tǒng)階數(shù)取為n=20，22，…，150，對(duì)n的每個(gè)取值進(jìn)行一次識(shí)別，運(yùn)行協(xié)方差驅(qū)動(dòng)隨機(jī)子空間法的MATLAB程序，提取(150-20)/2+1=66組頻率及振型數(shù)據(jù)，再將這些數(shù)據(jù)作為模糊聚類(lèi)算法FCM程序的輸入數(shù)據(jù)，以頻率為橫坐標(biāo)，MAC的第5列值(即簡(jiǎn)支梁第5節(jié)點(diǎn))為縱坐標(biāo)繪制FCM穩(wěn)定圖。噪聲水平分別為λs=1%、λs=5%和λs=10%的穩(wěn)定圖如圖3所示。

圖3中所示的穩(wěn)定圖將頻率與MAC數(shù)據(jù)點(diǎn)均分為10類(lèi)。圖中下方曲線為頻率譜密度(PSD)曲線，圓圈表示輸入數(shù)據(jù)點(diǎn)，五角星表示每一個(gè)聚類(lèi)的中心，十字表示每一類(lèi)中距離聚類(lèi)中心最近的數(shù)據(jù)點(diǎn)，10個(gè)最近數(shù)據(jù)點(diǎn)所對(duì)應(yīng)的頻率及振型即為識(shí)別的模態(tài)參數(shù)。

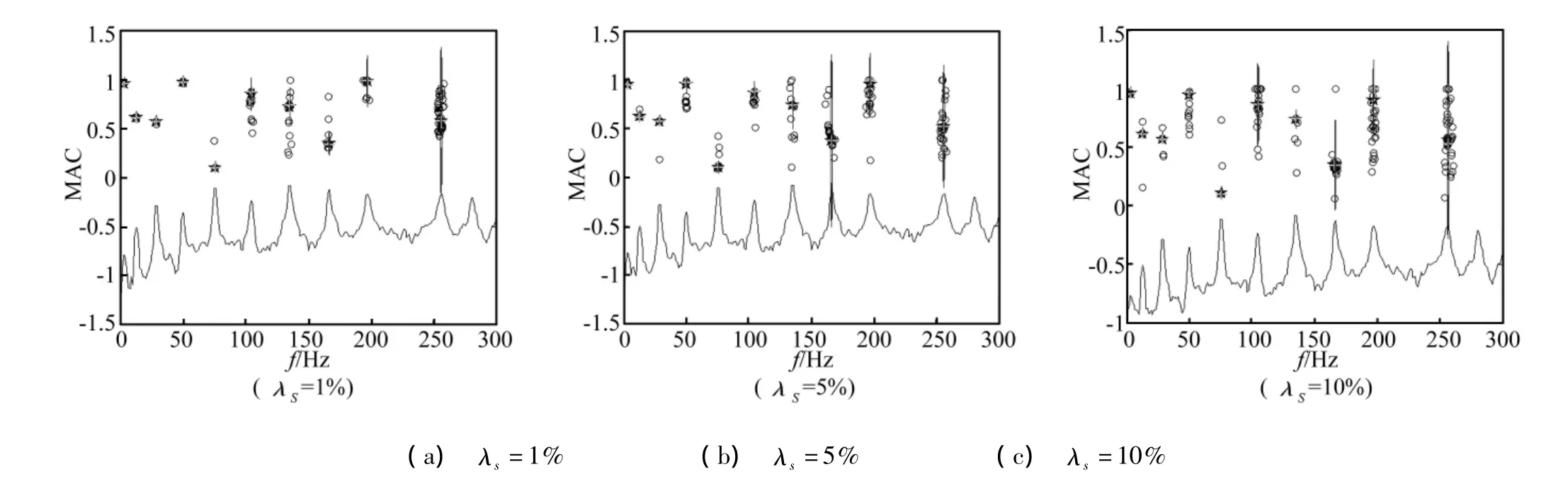
圖3 簡(jiǎn)支梁不同噪聲水平下的模糊聚類(lèi)穩(wěn)定圖Fig.3 Stabilization diagram with different noise levels of the simple beam

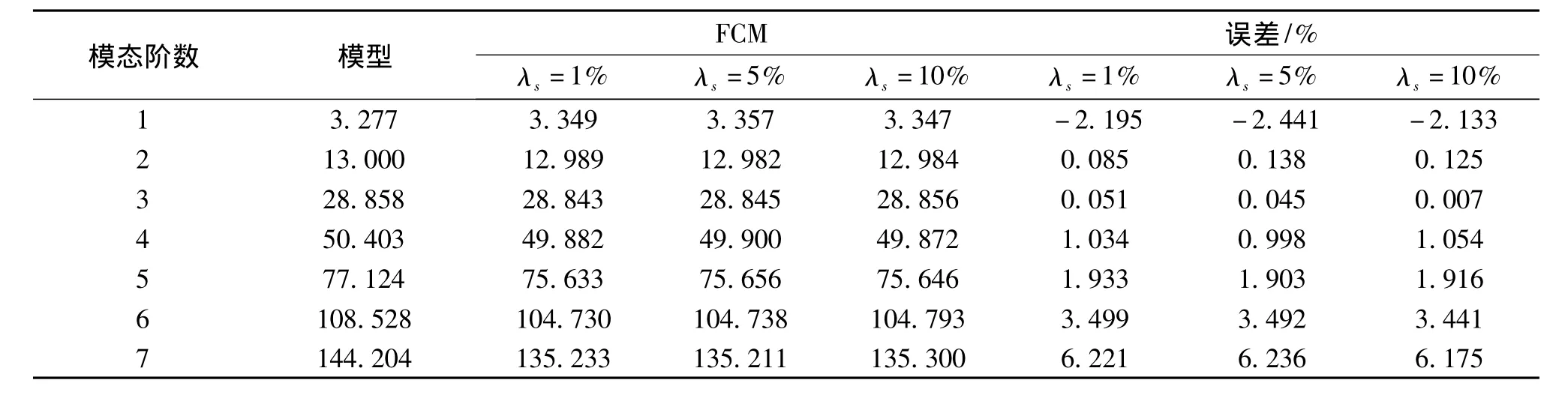
表1 簡(jiǎn)支梁頻率統(tǒng)計(jì)結(jié)果Tab.1 Frequency statistics of the simple beam

但是，圖3所示穩(wěn)定圖中識(shí)別的10階模態(tài)并不一定均為真模態(tài)，故需剔除其中的虛假模態(tài)。本文提出比較圓法，即計(jì)算每一聚類(lèi)所有數(shù)據(jù)點(diǎn)與聚類(lèi)中心距離的平均值，并以此平均值為半徑，以聚類(lèi)中心為圓心作圓，通過(guò)比較每一個(gè)聚類(lèi)所繪圓的大小即可剔除虛假模態(tài):圓越大(半徑越大)也就表征該聚類(lèi)分散，所對(duì)應(yīng)的模態(tài)參數(shù)結(jié)果越不準(zhǔn)確，更易識(shí)別到虛假模態(tài)。但由于圖3橫縱坐標(biāo)比例不同，圖中的圓看起來(lái)是偏橢圓或一條豎線，圖4給出了λs=1%時(shí)第1個(gè)聚類(lèi)橫縱坐標(biāo)采用相同比例的放大圖，從圖中可清晰地看到聚類(lèi)中心、距中心最近數(shù)據(jù)點(diǎn)以及聚類(lèi)圓的大小。

通過(guò)比較圖3中各聚類(lèi)圓的大小可知，識(shí)別到的前7階模態(tài)相對(duì)后3階模態(tài)可靠度更高，可判定為真。表1列出了穩(wěn)定圖中與各聚類(lèi)中心最近數(shù)據(jù)點(diǎn)對(duì)應(yīng)的前7階頻率的統(tǒng)計(jì)結(jié)果。

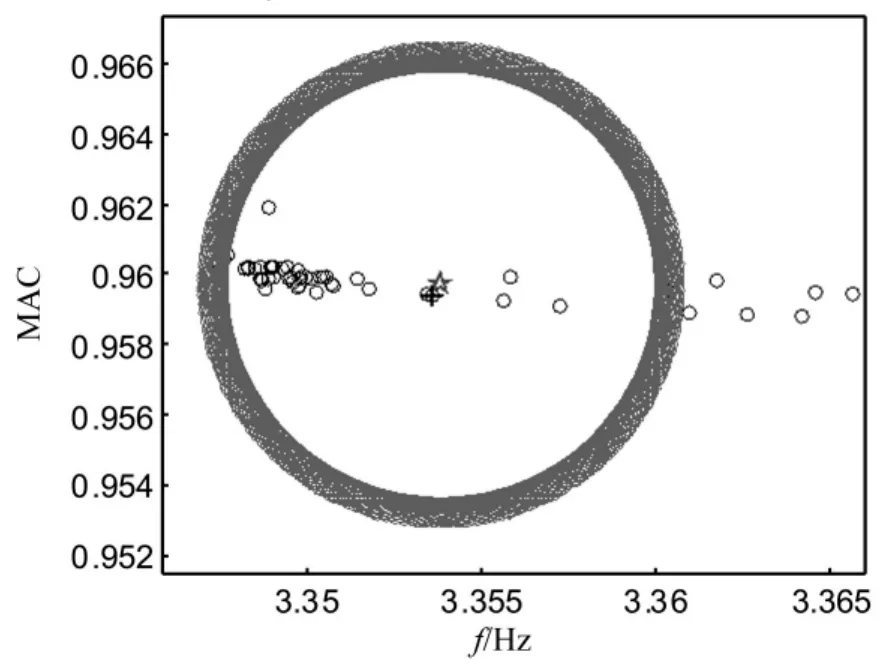
圖4 第一個(gè)聚類(lèi)放大圖Fig.4 Enlarged drawing of the first clustering

從表1可見(jiàn):(1)FCM穩(wěn)定圖識(shí)別的前7階頻率值與有限元模型相比，計(jì)算出的誤差最大為6.236%，可見(jiàn)FCM穩(wěn)定圖用于結(jié)構(gòu)參數(shù)識(shí)別具有較高的準(zhǔn)確性。(2)在應(yīng)變值中加入不同水平的噪聲時(shí)，模態(tài)參數(shù)的識(shí)別能力并沒(méi)有隨噪聲水平的增大而降低，說(shuō)明基于FCM穩(wěn)定圖的抗噪能力強(qiáng)。(3)不同噪聲水平識(shí)別的頻率與有限元模型結(jié)果的計(jì)算誤差均隨模態(tài)階數(shù)的增高而增大。

圖5給出了噪聲水平分別為λs=1%、λs=5%和λs=10%時(shí)FCM穩(wěn)定圖所識(shí)別的精度較高的前4階模態(tài)參數(shù)識(shí)別結(jié)果，并將有限元模型計(jì)算結(jié)果繪于圖5與穩(wěn)定圖識(shí)別結(jié)果進(jìn)行對(duì)比分析。

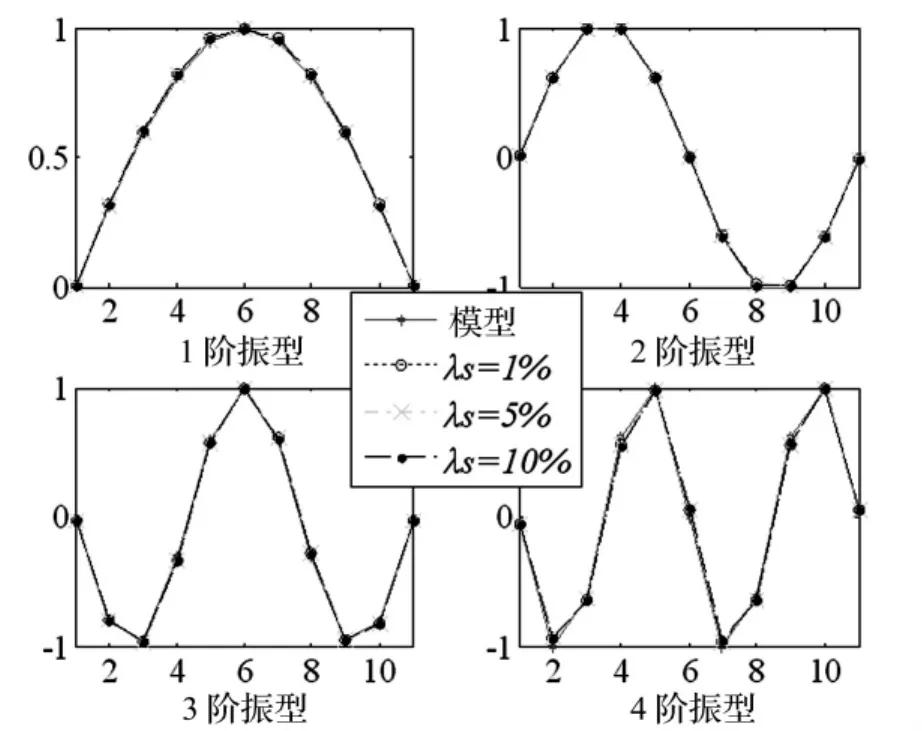
圖5 模糊聚類(lèi)穩(wěn)定圖識(shí)別振型Fig.5 Identified mode shapes with FCM stabilization diagram

從圖5可知，不同噪聲水平識(shí)別出的前4階模態(tài)振型結(jié)果相近，與有限元結(jié)果基本一致。由此可見(jiàn)，在白噪聲激勵(lì)來(lái)模擬現(xiàn)場(chǎng)環(huán)境激勵(lì)下，基于模糊聚類(lèi)算法的穩(wěn)定圖可以非常準(zhǔn)確且快速地對(duì)結(jié)構(gòu)模態(tài)參數(shù)進(jìn)行識(shí)別。

4.2 連續(xù)梁

為驗(yàn)證實(shí)模糊聚類(lèi)穩(wěn)定圖橋梁結(jié)構(gòu)在復(fù)雜的自然激勵(lì)情況下參數(shù)識(shí)別中的可靠性，對(duì)一座三等跨連續(xù)梁結(jié)構(gòu)進(jìn)行分析。橋梁全長(zhǎng)L=60m，截面高H=1.3 m，面積A=0.928 m2，慣性矩I=0.179 m4，材料密度 ρ=2 600 kg/m3，彈性模量E=35 GPa。連續(xù)梁有限元模型如圖6所示。

圖6 連續(xù)梁橋有限元模型Fig.6 Finite element model of the continuous beam

圖6中，向下的集中力(黑色箭頭)對(duì)橋梁施加時(shí)長(zhǎng)為2.401 s的移動(dòng)瞬時(shí)荷載，用來(lái)模擬汽車(chē)從橋左端移動(dòng)到右端的自然環(huán)境激勵(lì)。考慮了噪聲水平為λs=5%、λs=10%的兩種情況。采樣頻率1 000 Hz，運(yùn)行協(xié)方差驅(qū)動(dòng)的隨機(jī)子空間法程序，獲得n=20，52，…，150共66組識(shí)別到的模態(tài)參數(shù)值(頻率及MAC中第15列)，繪制FCM穩(wěn)定圖如圖7所示。

從圖7可以看出，穩(wěn)定圖中前幾階模態(tài)比較圓較大，由此可通過(guò)比較各聚類(lèi)圓的大小來(lái)剔除虛假模態(tài)。圖8給出了有限元模型計(jì)算及穩(wěn)定圖識(shí)別所得的前5階豎向應(yīng)變模態(tài)振型結(jié)果。前5階頻率的統(tǒng)計(jì)結(jié)果列于表2。

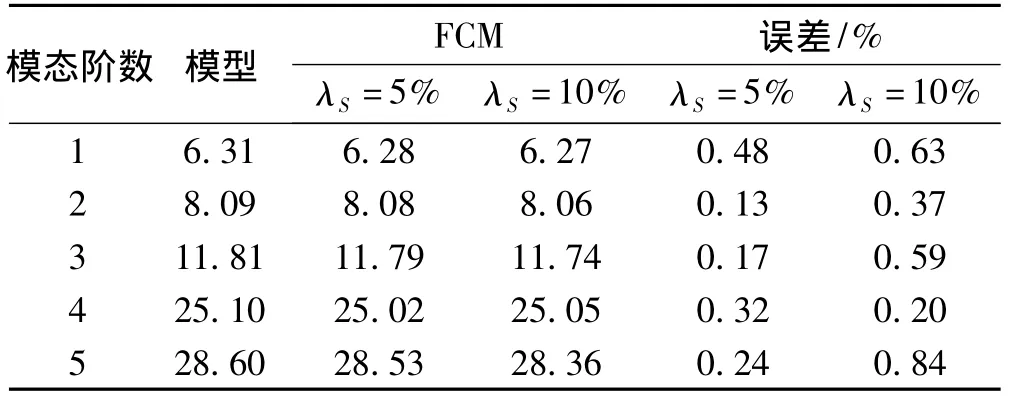
表2 連續(xù)梁頻率統(tǒng)計(jì)結(jié)果Tab.2 Frequency statistics of the continuous beam

由圖8可知，在移動(dòng)荷載激勵(lì)下，除噪聲水平為10%時(shí)識(shí)別的第1階振型與有限元結(jié)果相差較大外，其余振型結(jié)果均與模型結(jié)果相近。表2中不同噪聲水平穩(wěn)定圖識(shí)別的前5階頻率也均與模型結(jié)果非常接近，最大誤差不超過(guò)1%。由此，進(jìn)一步驗(yàn)證了本文提出的模糊聚類(lèi)穩(wěn)定圖應(yīng)用于橋梁結(jié)構(gòu)參數(shù)識(shí)別的可靠性和有效性。

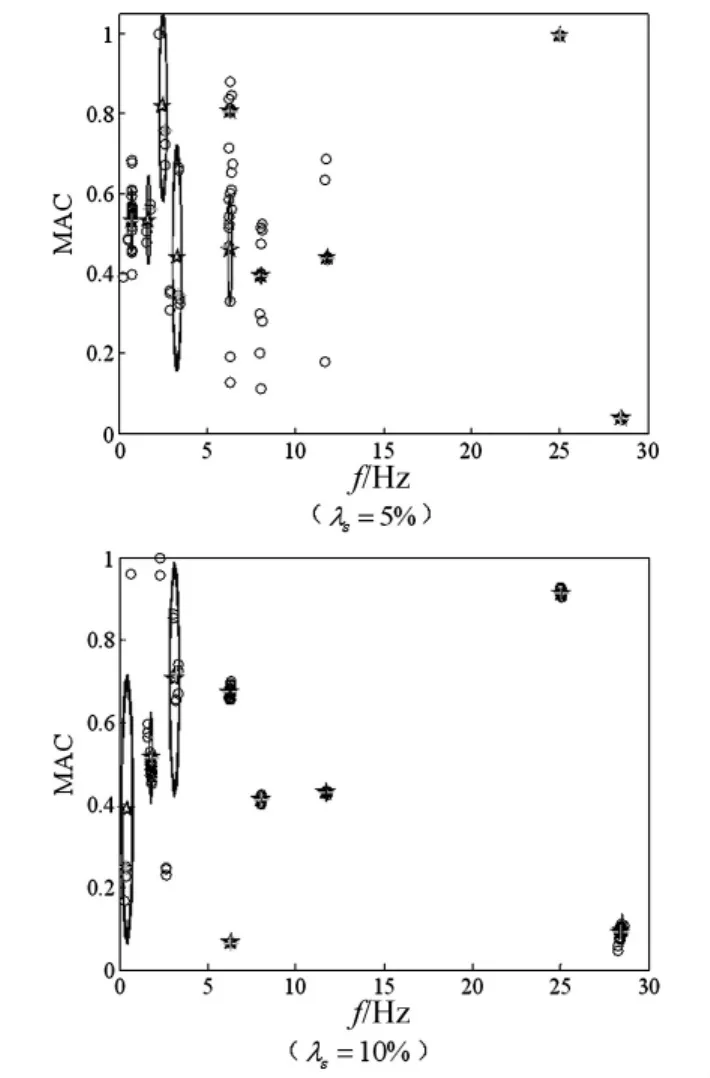
圖7 連續(xù)梁模糊聚類(lèi)穩(wěn)定圖Fig.7 Stabilization diagram of the continuous beam

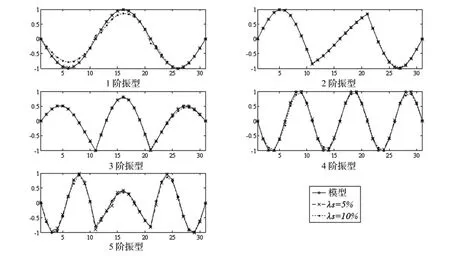
圖8 連續(xù)梁FCM穩(wěn)定圖識(shí)別結(jié)果Fig.8 Identified results based on FCM stabilization diagram of the continuous beam

5 結(jié)論

將模糊聚類(lèi)算法應(yīng)用于穩(wěn)定圖理論，并將該穩(wěn)定圖與協(xié)方差驅(qū)動(dòng)的隨機(jī)子空間法相結(jié)合對(duì)橋梁結(jié)構(gòu)參數(shù)識(shí)別進(jìn)行研究，得到以下結(jié)論:

(1)以頻率為橫坐標(biāo)，以MAC中的任一列數(shù)據(jù)為縱坐標(biāo)的模糊聚類(lèi)算法穩(wěn)定圖與協(xié)方差驅(qū)動(dòng)的隨機(jī)子空間法相結(jié)合可準(zhǔn)確識(shí)別結(jié)構(gòu)模態(tài)參數(shù)。

(2)通過(guò)比較圓法，使穩(wěn)定圖真假模態(tài)的判別不再需要人的主觀參與而變得更加智能和準(zhǔn)確，使參數(shù)識(shí)別技術(shù)實(shí)現(xiàn)自動(dòng)化。

(3)通過(guò)在簡(jiǎn)支梁和和連續(xù)梁的測(cè)量信號(hào)中加入不同噪聲水平后發(fā)現(xiàn)，無(wú)論是在白噪聲激勵(lì)下還是在移動(dòng)荷載激勵(lì)下，F(xiàn)CM穩(wěn)定圖均能準(zhǔn)確地識(shí)別結(jié)構(gòu)模態(tài)參數(shù)，說(shuō)明本文提出方法具有較強(qiáng)的抗干擾性能。

［1］彭細(xì)榮，路新瀛，陳肇元.結(jié)構(gòu)應(yīng)變模態(tài)識(shí)別的隨機(jī)子空間方法［J］.振動(dòng)與沖擊，2008，27(6):4-6.

PENG Xi-rong，LU Xin-ying，CHEN Zhao-yuan.Stochastic subspace method for structuralstrain modalparameter identification［J］.Journal of Vibration and Shock，2008，27(6):4-6.

［2］Jansson M，Wahlberg B，A linear regression approach to statespace subspace system identification［J］.Signal Processing，1996，52:103-129.

［3］樊可清，倪一清，高贊明.改進(jìn)隨機(jī)子空間系統(tǒng)辨識(shí)方法及其在橋梁狀態(tài)監(jiān)測(cè)中的應(yīng)用［J］.中國(guó)公路學(xué)報(bào)，2004，17(4):70-73.

FAN Ke-qing， NIYi-qing， GAO Zan-ming. Improved stochastic system identification approach with its application in bridge condition monitoring.China Journal of Highway and Transport，2004，17(4):70-73.

［4］Reynders E，Pintelon R，De Roeck G.Uncertainty bounds on modal parameters obtained from stochastic subspace identification［J］.Mechanical Systems and Signal Processing 2008，22:948-969.

［5］Alicioglu B，Lus H，Asce A M，Ambient vibration analysis with subspace methods and automated mode selection:case studies［J］.Journal of Structural Engineering，2008:1016-1029.

［6］常 軍，孫利民，張啟偉.基于兩階段穩(wěn)定圖的隨機(jī)子空間識(shí)別結(jié)構(gòu)模態(tài)參數(shù)［J］.地震工程與工程振動(dòng)，2008，28(3):47-51.

CHANG Jun，SUN Li-min，ZHANG Qi-wei.Study on the method for stochastic subspace identifying structural modal parameters based on two-stage stabilization diagram［J］.Journal of Earthquake Engineering and Engineering Vibration，2008，28(3):47-51.

［7］Fan J L，Zhang Z Y，Hua H X.Data processing in subspace identification and modal parameter identification of an arch bridge［J］.Mechanical Systems and Signal Processing，2007，21:1674-1689.

［8］ Scionti M，Lanslots J P. Stabilisation diagrams:Pole identification using fuzzy clustering techniques［J］.Advances in Engineering Software，2005，36:768-779.