一類具有時滯的病毒自發(fā)變異的傳染病模型

仝耀華，李錄蘋

（山西大同大學數學與計算機科學學院，山西 大同 037009）

一類具有時滯的病毒自發(fā)變異的傳染病模型

仝耀華，李錄蘋

（山西大同大學數學與計算機科學學院，山西 大同 037009）

考慮一類具有時滯的病毒自發(fā)變異的傳染病模型，就無病平衡點的局部穩(wěn)定性和全局穩(wěn)定性進行了詳細的分析。

時滯；傳染病模型；平衡點；穩(wěn)定性

在現實生活中有些常見的傳染病往往隨著病情的發(fā)展，病毒自身會發(fā)生變異，從而導致不同階段的病毒具有不同的傳染力。根據文獻[1-2]給出了的傳染病模型：

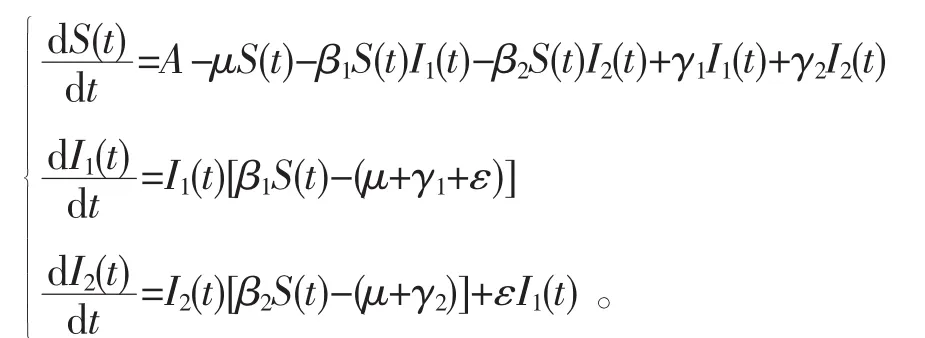
假設所有輸入者都是t時刻易感者，數量為S=S（t）。把所有感染者分為兩類：一類為t時刻變異前病毒感染患者，數量為I1=I1（t），簡稱為變異前患者，治愈后又成為易感者，同時有部分變異前患者未能治愈而發(fā)展成變異后患者；一類為t時刻變異后病毒感染患者，數量為I2=I2（t），簡稱為變異后患者，治愈后也又成為易感者。這兩類患者均具有傳染力，同時假設疾病不足以導致死亡。

其中A表示總人群的輸入率，μ表示自然死亡率；β1和β2分別表示變異前患者和變異后患者的傳染率系數；γ1和γ2分別表示變異前患者和變異后患者的恢復率系數；ε表示變異前患者發(fā)展為變異后患者的速率系數。所有參數均為正。

基于對上述模型的的研究，結果表明：當變異前患者和變異后患者的基本再生數均不超過1時，疾病會最終滅絕；當變異前患者的基本再生數小于變異后患者的基本再生數，且至少有一個大于1時，最終只會在變異后患者存在；當變異前患者的基本再生數大于變異后患者的基本再生數，同時還大于1時，變異前患者和變異后患者會以某一確定的量共存于人群之中。

而有些時候，病毒由變異前到變異后會有一個時間差τ，所以在上述所有假設不變的情況下建立如下模型：

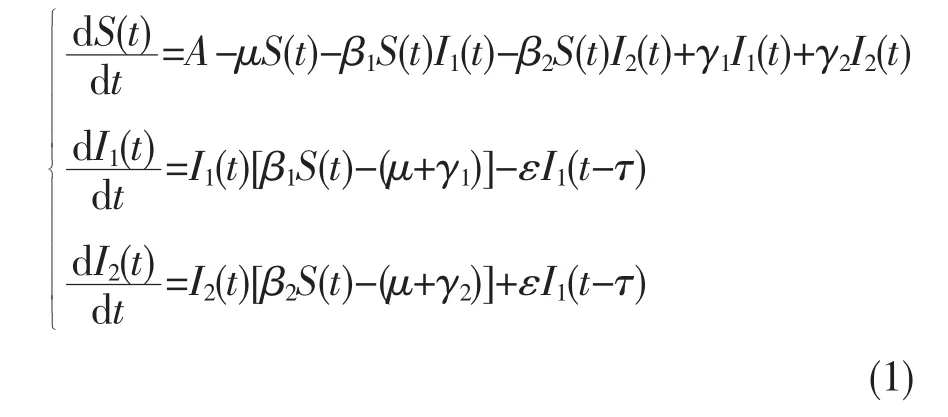
令N（t）=S（t）+I1（t）+I2（t），

則有

將S（t）=N（t）-I1（t）-I2（t）代入傳染病模型（1）中的第二個和第三個方程，

可得

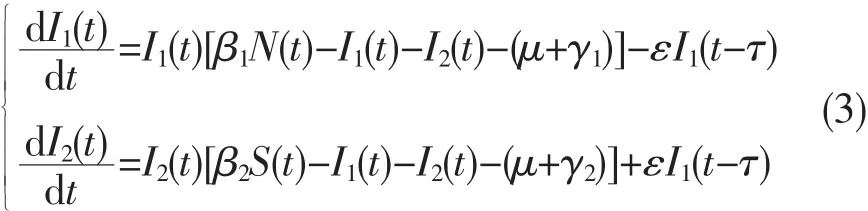
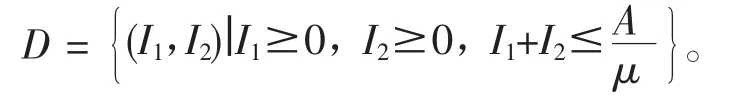
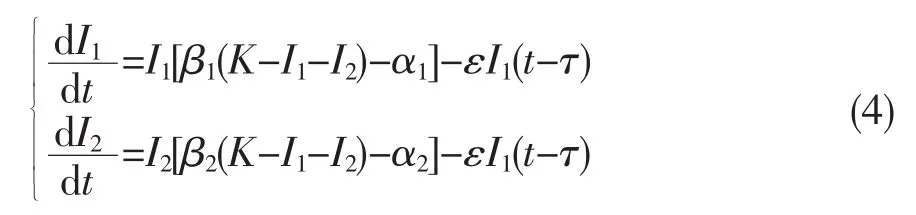
對于平衡點的分析

首先討論非負平衡點的穩(wěn)定性。

若條件

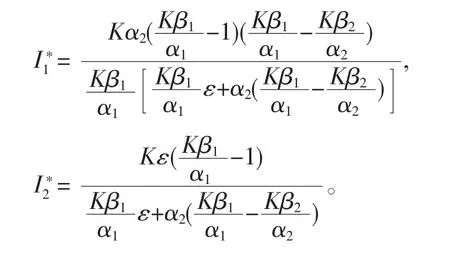
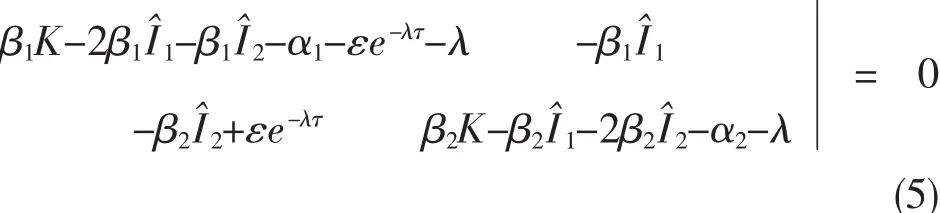
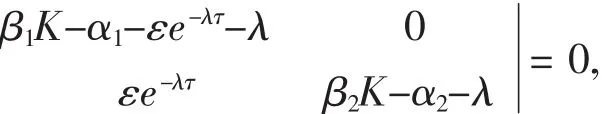
[λ-（β1K-α1-εe-λτ][λ-（β2K-α2]=0,

則有

（Ⅰ）當β2K-α2＜0且β1K-α1-ε＜0時，無病平衡點E0（0，0）是局部漸近穩(wěn)定的。

（Ⅱ）當β2K-α2＞0或β1K-α1-ε＞0時，無病平衡點E0（0，0）是鞍點。

另外，通過構造適當的Lyapunov函數，還可以得到無病平衡點E0（0，0）的全局漸近穩(wěn)定性。

定理1若β2K-α2＜0且β1K-α1＜0成立時，無病平衡點E0（0，0）是全局漸近穩(wěn)定的。證明構造Lyapunov函數

V=I1+I2,

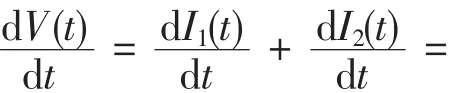
沿著極限系統(tǒng)（4）對求導數得I1（t）β1K-I21（t）-I1（t）I2（t）-α1I1（t）+ I2（t）β2K-I1（t）I2（t）-I22（t）-α2I2（t）≤I1β1K-α1I1+I2β2K-α2I2≤0。

而V=0當且僅當（I1，I2）=（0，0），則無病平衡點E0（0，0）是全局漸近穩(wěn)定的。證畢。

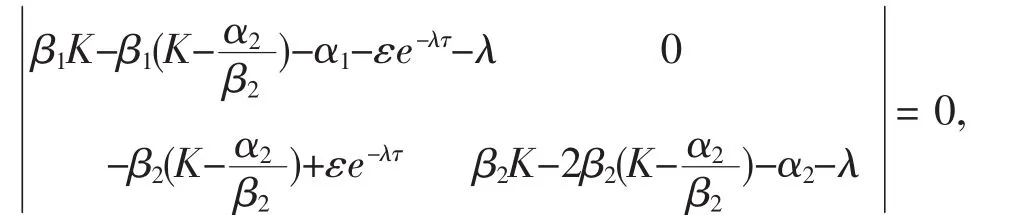
即

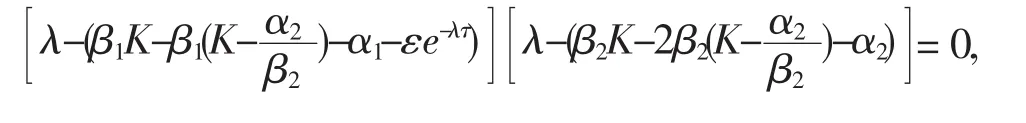
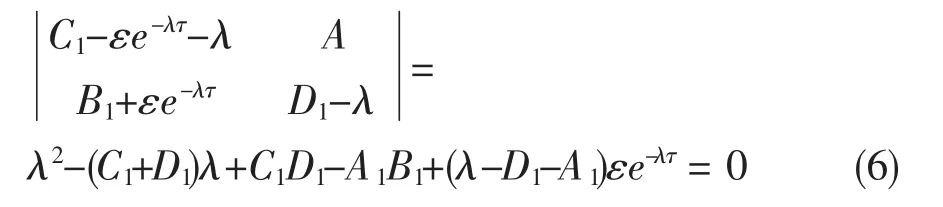
A1=-β1I1，B1=-β2I2，

C1=β1K-2β1I1-β2I2-α1，

D1=β2K-β2I1-2β2I2-α2,

【1】τ=0

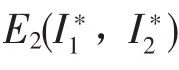
【2】τ≠0,

考慮下面特征方程

P和Q分別為n次和m次的實系數多項式，τ是非負常數。Cooke等[3-4]已得到如下結果：

引理1考慮特征方程（8），其中P和Q是λ在右半平面Reω＞-δ，δ＞0的解析函數，若滿足如下假設

（1）P和Q沒有共同的純虛根；

（3）P（0）+Q（0）≠0；

（4）當τ=0時，方程（8）的右平面至多有有限個根；

（5）對任意實數y，方程F（y）=｜P（iy）｜2-｜Q（iy）｜2至多有有限個實根。

則有下面的結論

（a）若方程F（y）=0沒有正根，則當τ=0時，若系統(tǒng)（8）穩(wěn)定，則對所有的τ≥0仍然是穩(wěn)定的。

（b）若方程F（y）=0至少有一個正根且每個正根都是單根，則隨著τ值的增加，系統(tǒng)（8）將會發(fā)生穩(wěn)定性開關現象，即存在一個正數τ*，當τ＞τ*時，系統(tǒng)（8）是不穩(wěn)定的。當τ從0到τ*改變時，系統(tǒng)（8）至多存在著有限個穩(wěn)定性開關。

把方程（6）重新寫成下面的形式

其中P（λ）=λ2-（C1+D1）λ+C1D1-A1B1，Q（λ）=ελ－（D1+ A1）ε，容易驗證系統(tǒng)（9）滿足引理1的條件（5），為了考察非負平衡點E2，）的穩(wěn)定性，需要分析下面方程存在正根的情況：

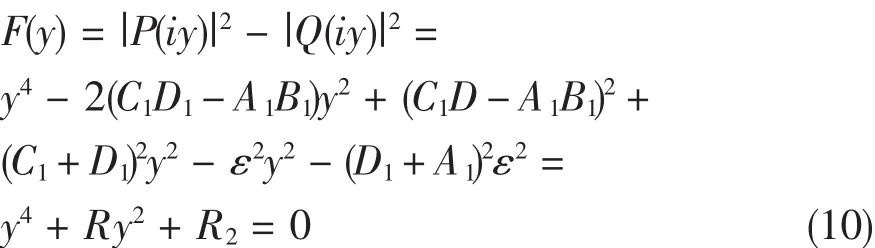
其中

R1=-2（C1D1-A1B1）+（C1+D1）2-ε2，

R2=（C1D-A1B1）2-（D1+A1）2ε2，

則方程（10）的正根有下面兩種情形：

令z＝y(tǒng)2，并記

h（z）=z2+R1z+R2,

則

△=R21-4R2。

命題1若△=R21-4R2＜0，F（y）=0，則方程（10）沒有正根。

命題2若△=R21-4R2＜0，h（0）≥0，F（y）=0，則方程（10）至少有一個正根且為單根。

由于當τ=0時，非負平衡點E2，）是局部漸近穩(wěn)定的，所以可以由命題1和命題2及引理1得到下面的結果：

[1]馬知恩.生態(tài)學的數學建模與研究[M].合肥：安徽教育出版社，2001.

[2]楊亞莉，李健全.一類病毒自身發(fā)生變異的權無染病模型的全局分析[J].生物數學學報，2008，23（1）：102-106.

[3]Cooke K L，van den Driessche.On zeros of some transcendental equations[J].Funkcial Ekvac，1986（29）：87-90.

[4]李銳，薛亞奎.一類具有非線性傳染率的時滯SIR模型的分析[J].數學實踐與認識，2009，39（15）：98-104.

〔責任編輯 高 海〕

The Time Delay Epidem ic Modelw ith Spontaneous Virus Variation

TONG Yao-hua,LILu-ping
（School ofMathematics and Computer Science,ShanxiDatong University,Datong Shanxi,037009）

This paper considers a time delay epidemic model with spontaneous virus variation.It analyzes the local and global stability of disease-free equilibrium point in detail.

time delay；epidemicmodel；equilibrium point；stability

O212.4

A

2013-05-15

仝耀華（1979-），女，山西大同人，碩士，講師，研究方向：生物數學。

1674－0874（2013）05－0020－03