完全對換網絡的容錯性

師海忠，王國亮

(西北師范大學數學與數學統計學院，蘭州 730070)

互連網絡是并行處理系統的重要組成部分。互連網絡常被模型化為一個無向圖，圖的頂點對應處理機，圖的邊對應網絡的通訊連線［1-3］。1989 年 S.B.Akers等［8］提出了互連網絡群模型，1998年師海忠［5］提出了互連網絡環模型，并于2011年又提出了互連網絡向量圖模型［7］。完全對換網絡是利用群模型設計出來的一類互連網絡。容錯性是互連網絡的一個重要性質。互連網絡的容錯性是指該網絡能容忍多少組件或連線同時發生故障，剩余的子網絡中仍然含有某些特殊結構并能正常工作。基于此，Becker和Simon等［12-14］研究了在n維超級立方體網絡中使每個(n-k)維子立方體網絡失靈的失靈邊的最小數目fH(n，k)，并給出了相關結果。Latifi等［9-11］研究了在n維星網絡中使每個(n-k)維子星網絡失靈的失靈點和失靈邊的最小數目Fs(n，k)和fs(n，k)，并給出相關結果。隨后，Shiying Wang等［15］研究了在 n維冒泡排序網絡中使每個(n-k)維子冒泡排序網絡失靈的失靈點和失靈邊的最小數目FB(n，k)和fB(n，k)，并給出了相關結果。本文研究在n維完全對換網絡中使每個(n-k)維子完全對換網絡失靈的失靈點和失靈邊的最小數目，分別記為FCT(n，k)和 fCT(n，k)。

1 概念及基本性質

定義1 設G是一個有限群，e是它的單位圓，Ω={g1，g2，…，gn}是 G 的一個生成子集且滿足:1)gi∈Ω?g-1i∈Ω;2)e?Ω。Cayley圖 Γ=(G，Ω)是一個簡單圖，它的頂點集和邊集分別如下［2］:

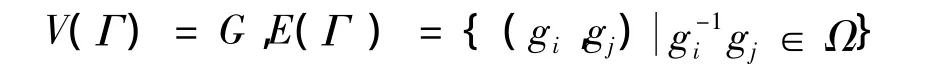
定義2 一個對換就是指交換2個數的位置所得的置換。對換圖是一個無環圖，它有n個頂點，分別用符號 1，2，…，n 來表示，它的邊(i，j)對應于一個對換，即在1，2，…，n中把i和j交換得到的置換，稱這個圖為對換圖［6］。

定義3 完全對換網絡是特殊的Cayley圖Γ(Sn，Ω)，其中Sn是n 個符號1，2，…，n 上的對稱群，Sn的生成集 Ω={(i，j)1≤i＜j≤n，(這里(i，j)表示交換i和j的位置得到的置換)}，即Ω對應的對換圖為n階完全圖［4］，簡記為CTn。完全對換網絡CT3和CT4如圖1所示。

性質1 完全對換網絡CTn有n!個頂點，n(n-1)n!/4條邊，且是 n(n-1)/2正則二部圖，它是頂點可遷和邊可遷的，其直徑為n-1。

令 Λn為符號集{1，2，…，n-1，n，X}，其中 X表示與數字不相關的符號。CTn的每個子完全對換網絡能被Λn中的字符串通過重復X唯一表示。顯然，符號X的數目決定了子完全對換網絡的維數。例如X3X2X是一個子完全對換網絡CT3，它包含了以下 6 個頂點:{13425，13524，43125，43521，53124，53421}，共有 n種方法劃分 CTn為 n個不相交的CTn-1，即通過固定第1到第n位的數字來實現。

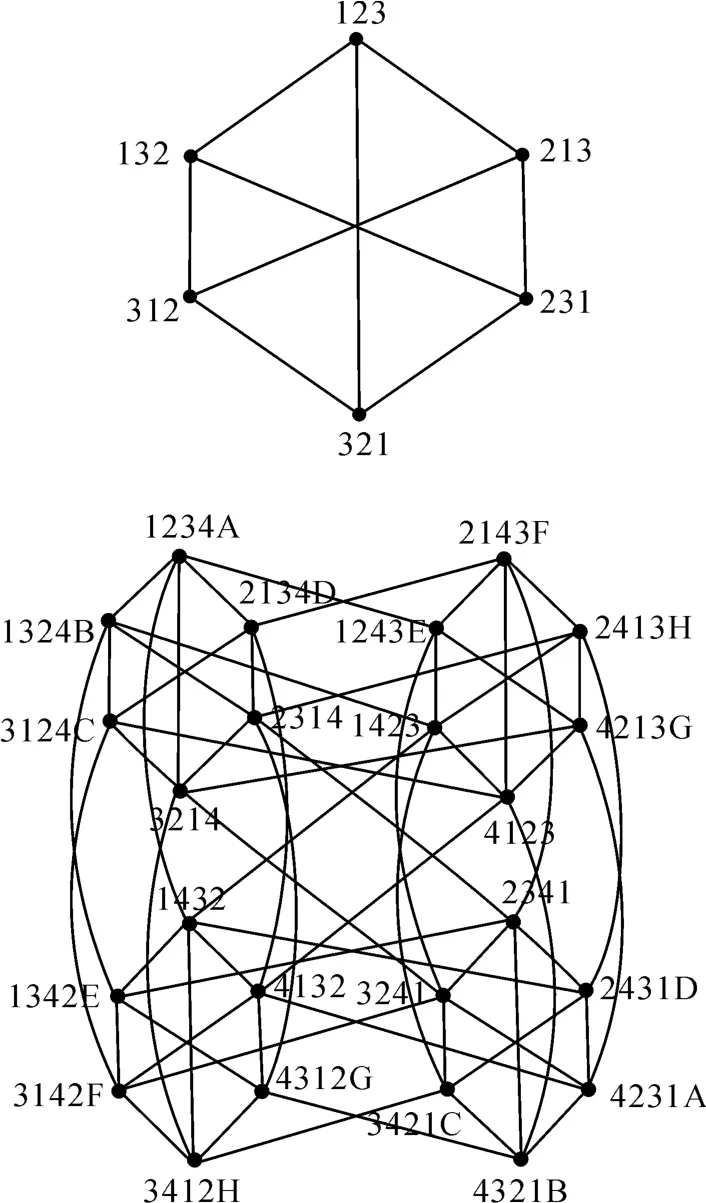
圖1 完全對換網絡CT3和CT4(相同字母的邊被省去)

2個CTn-k在CTn中是不相交的，如果它們沒有共同的頂點;2個CTn-k在CTn中是不相同的，如果它們的頂點集不同。根據以上定義，可以得到如下重要性質:

性質2 給定 2個整數 n≥1，k∈{0，1，…，n-1}，則在CTn中含有k!個不相交的CTn-k和k!個不相同的 CTn-k。這里=表示從n個物體中取出k個物體的組合數。

證明 當k=0時，顯然成立。下證當k≥1時結論成立。根據2個CTn-k在CTn中是不相交的定義可知:從n個數中取出k個數，并把這k個數全排列，其余(n-k)個數均為X，則構成的CTn-k沒有相同的頂點，即共有 k!個不相交的。根據2個CTn-k在CTn中是不相同的定義可知:把上述取出的k個數放在n個位置中的第k個位置上，共有種放法。則構成CTn-k的頂點集不同，即共有k!個不相同的CTn-k。

2 主要結果

fCT(n，k)(或 FCT(n，k))表示在 n 維完全對換網絡CTn中，使每個(n-k)維子完全對換網絡失靈的失靈邊(或點)的最小數目。為了以下引理的完整性，令fCT(n，n-1)=+∞。由性質2可得如下引理:

引理1 給定一個整數 k∈{0，1，…，n-1}，則k!≤FCT(n，k)≤fCT(n，k)≤k!。

證明 由性質2可知，CTn中含有k!個不相交的CTn-k，若使所有不相交的CTn-k失靈，則在每個CTn-k中須至少出現1個失靈點，故k!≤FCT(n，k)。令F是一個在CTn中使每個CTn-k失靈的失靈邊最小數目的邊集，對F中的每條邊，可以選取每條邊上的一個頂點，則個失靈點可以使CTn中所有 CTn-k失靈，故 FCT(n，k)≤=fCT(n，k)，fCT(n，k)的上界可以通過使每個 CTn-k中的一條邊失靈得到。結合以上不等式得:k!≤FCT(n，k)≤fCT(n，k)≤k!。

以下定理給出FCT(n，k)和fCT(n，k)在一些特殊情況下的精確值。

定理1 CTn是n維完全對換網絡，則

1)FCT(n，0)=fCT(n，0)=1;

2)FCT(n，1)=n;

3)當 n≥2 時，FCT(n，n-1)=n!;

4)當 n≥3 時，FCT(n，n-2)=n!/2;

5)當n≥2 時，fCT(n，n-2)=n(n-1)n!/4。

證明

1)CTn中的任意一條邊都能使CTn失靈，則fCT(n，0)≤1。由引理 1 知:fCT(n，0)≥1，故 FCT(n，0)=fCT(n，0)=1;

2)由性質2知:在CTn中含有n2個不相同的CTn-1，頂點 123…n將使 n個 CTn-1即 1Xn-1，X2Xn-2，X23Xn-3，…Xn-1n 都失靈;對每個 2≤i≤n-1，頂點i(i+1)…n1…(i-1)將使 n個CTn-1即 iXn-1，X(i+1)Xn-2，X2(i+2)Xn-3，…，Xn-1(i-1)都失靈;頂點n12…(n-1)將使n個CTn-1即nXn-1，X1Xn-2，X22Xn-3，…Xn-1(n-1)都失靈。這樣 FCT(n，1)≤n，由引理 1 知:FCT(n，1)≥n，故FCT(n，1)=n。

3)給定一個整數n≥2。事實上，要使CTn中的每個CT1失靈，則須使CTn的所有點失靈，故FCT(n，n-1)=n!。

4)給定一個整數n≥3。令(Y，V(CTn)Y)是CTn的一個二部劃分，Y中的每個頂點失靈保證了CTn中的所有CT2失靈，則FCT(n，n-2)≤n!/2，由引理1 知:FCT(n，n-2)≥n!/2，故 FCT(n，n-2)=n!/2。

5)給定一個整數n≥3。要使CTn中所有CT2失靈，實際上就是使CTn中所有邊都失靈，故fCT(n，n-2)=n(n-1)n!/4。

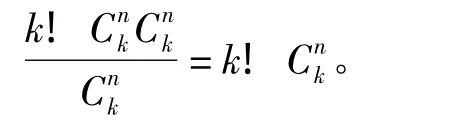
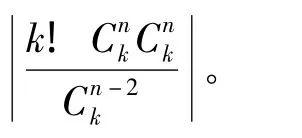
定理2 當 n=4或 n=5時，fCT(n，1)=n+4。

證明 當n=4時，可以找到以下8條失靈邊使CT4中所有 CT3失靈，失靈邊如下:1XX2，XX23，X23X，23XX，3XX4，XX41，X41X，41XX，則fCT(4，1)≤8。由引理3 知:fCT(4，1)≥8，故 fCT(4，1)=8。當n=5時，可以找到以下9條邊使CT5中所有 CT4失靈，失靈邊如下:1X2X3，X2X34，2X34X，X34X5，34X5X，4X5X1，X5X12，5X12X，X12X3，則 fCT(5，1)≤9。由引理 3 知:fCT(5，1)≥9，故 fCT(5，1)=9。

綜上所述，當 n=4或 n=5時，fCT(n，1)=n+4。

當n≥6時，定理3將給出 fCT(n，1)的精確值，為了更好地理解定理3的證明過程，首先給出如下例子:

例1 當n=7時，使CT7中所有CT6失靈的失靈邊見表1。

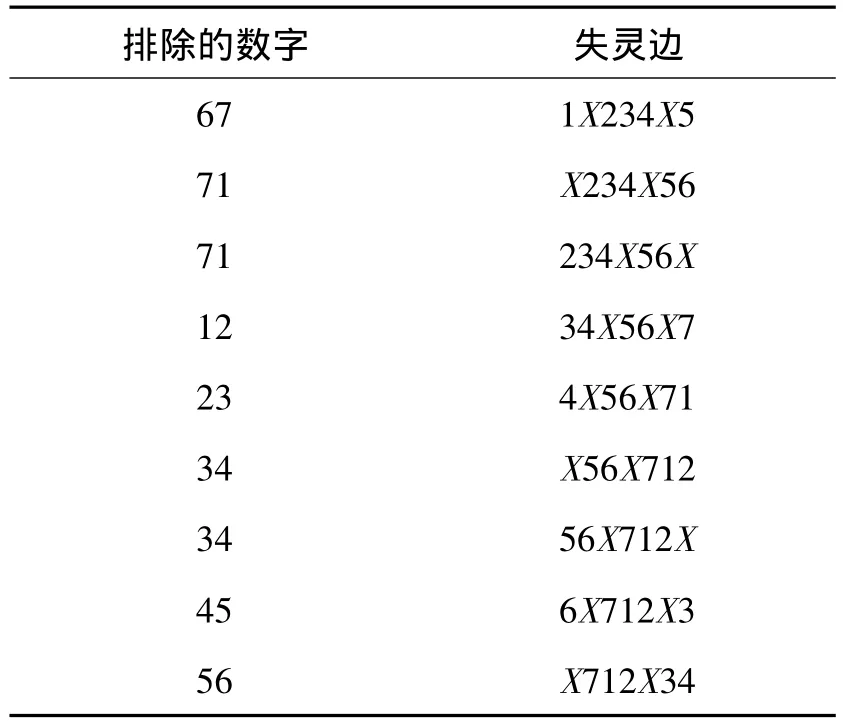
表1 失靈邊

由表1可以看出，后一條失靈邊是由前一條失靈邊按下述方式得到:

1)當失靈邊的第1位是X時，后一條失靈邊由該失靈邊作個循環即可。例如:前一條失靈邊為X234X56，后一條失靈邊由該失靈邊作個循環，即為234X56X。

2)當失靈邊的第1位不是X時，后一條失靈邊由該失靈邊從第2位開始，各個位上的X或數字都向前移動一位，最后一位數字填上從后往前的第1位數字加1(注意:當該數字為7+1時取為1)。最后，當2個X第2次分別位于第(7-3)和第7位時停止。

根據性質2知:完全對換網絡CT7中含有49個不相同的CT6，該表的前9條失靈邊使CT7中的45個CT6失靈，而最后一條邊使余下的4個CT6失靈，所以這10條邊可使CT7中的所有CT6都失靈，即 fCT(7，1)≤10。又由引理 3知:fCT(7，1)≥10，故 fCT(7，1)=10。

更一般地，對任意整數n≥6，有如下定理:

定理3 當n≥6時，fCT(n，1)=n+3。

證明 通過以下方法構造使CTn中所有CTn-1失靈的失靈邊最小數目的邊集。

第1步 首先選擇1X23…(n-3)X(n-2)作為失靈邊。

第2步 后一條失靈邊是由前一條失靈邊得到，具體方法如下:

1)當失靈邊的第1位是X時，后一條失靈邊由該失靈邊作個循環即可。例如:前一條失靈邊為X234X56，后一條失靈邊由該失靈邊作個循環，即為234X56X。

2)當失靈邊的第1位不是X時，后一條失靈邊由該失靈邊從第2位開始各個位上的X或數字都向前移動1位，最后一位數字填上從后往前的第1位數字加1(注意:當該數字為n+1時取為1)。

第3步 當2個X第2次分別位于第(n-3)和第n位時停止。

引理4 當 n是素數時，Fs(n，2)=n(n-1)［10］。這里，Fs(n，2)是使 Sn中所有 Sn-2失靈的失靈點的最小數目。

當n是素數，k=2時，定理4將給出FCT(n，2)的精確值，為了更好地理解定理4的證明過程，給出下面的例子。

例2 當n=5，k=2時，使完全對換網絡CT5中所有CT3失靈的失靈點構造如下:選擇標號為(1，1+I，1+2I，1+3I，1+4I)的頂點，其中 1≤I≤4。當括號里的數字超過5時，取其模5的值。由以上選擇，可得到以下 4個頂點{(12345)，(13524)，(14253)，(15432)}，讓這4 個頂點都循環繞動一周，則每個頂點可生成5個標號不同的頂點，這4個頂點共生成20個標號不同的頂點，這20個頂點作為星網絡S5中的失靈點時，每個頂點可使S5中的6個S3失靈，但作為完全對換網絡CT5的失靈點時，每個頂點可使CT5中的10個CT3失靈(因為星網絡的第1位總是X)，故這20個頂點可使CT5中的200個CT3失靈，即FCT(5，2)≤20。由引理2知:由于 FCT(5，2)≥20，因此FCT(5，2)=20。

更一般地，當n是素數，k=2時，有如下定理:

定理4 當n是素數時，FCT(n，2)=n(n-1)。

證明 通過以下方法構造失靈點集。

第1 步 選取標號為(1，1+I，1+2I，…，1+(n-1)I)的頂點，其中1≤I≤n-1。當括號里的數字超過n時，取其模n的值。

第2步 讓上一步中所得的每個頂點都循環繞動一周。

通過以上方法共得到n(n-1)個標號不同的頂點，這n(n-1)個頂點作為Sn中的失靈點時，每個頂點可使個Sn-2失靈，而這n(n-1)個頂點作為CTn中的失靈點時，每個頂點可使個CTn-2失靈，即CTn中的每個失靈點比Sn中的每個失靈點多失靈()個。由引理4知:這n(n-1)個頂點可使 Sn中2!個 Sn-2失靈，所以這 n(n-1)個頂點可使 CTn中的 2!個失靈，而CTn中共有2!個CTn-2，即這n(n-1)個頂點可使CTn中所有的 CTn-2失靈，也就是說，FCT(n，2)≤n(n-1)。由引理 2 知:FCT(n，2)≥n(n-1)，故 FCT(n，2)=n(n-1)。

猜想 當0≤k≤n-1時，FCT(n，k)=k!

由以上定理知:該猜想對 k=0，1，n-2，n-1成立;對k=2，n為素數時也成立。

當k=2時，如下定理給出了 fCT(n，2)與fS(n，2)之間的關系。

定理5 對任意素數n，fCT(n，2)=fS(n，2)+2n(n-1)，這里 fCT(n，2)是使 CTn中所有 CTn-2失靈的失靈邊的最小數目，fS(n，2)是使Sn中所有Sn-2失靈的失靈邊的最小數目。

證明 由文獻［9］知，若把使Sn中所有Sn-2失靈的失靈邊排成1個矩陣，這個矩陣的行數為失靈邊的最小數目，這個矩陣的列數為n，并且這個矩陣有如下特性:除這個矩陣的第1列外，從其余(n-1)列中任意選取2列，選取的這2列中都將出現的所有組合數。同樣，若把使CTn中所有CTn-2失靈的失靈邊排成一個矩陣，這個矩陣的行數為失靈邊的最小數目，這個矩陣的列數為n，并且這個矩陣有如下特性:從這這個矩陣n列中任意選取2列，選取的這2列中都將出現的所有組合。若把Sn中使所有Sn-2失靈的失靈邊作為CTn中使CTn-2失靈的失靈邊時，則在CTn中共有n(n-1)(n-2)個CTn-2沒有失靈，且在CTn失靈邊的最小數目組成的矩陣中，沒有出現的組合數的列數為:第1列和第2列，第1列和第3列，第1列和第4列…，第1列和第 n列。選取以下邊集:

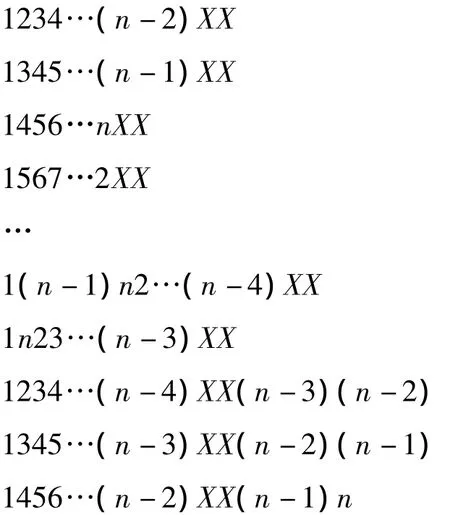
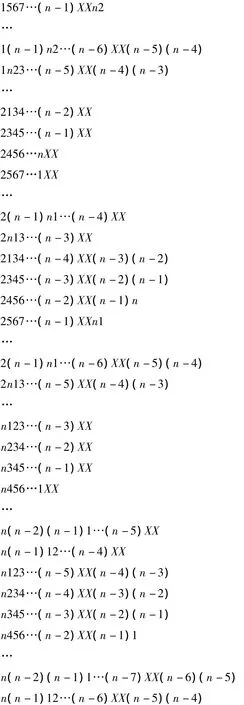
從以上邊集可以看出:在前n(n-1)條邊中，每條邊可以使個CTn-2失靈，這n(n-1)條邊共使n(n-1)(n-3)個CTn-2失靈;在后n(n-1)條邊中，每條邊可以使個 CTn-2失靈，這n(n-1)條邊共使2n(n-1)個 CTn-2失靈，即這2n(n-1)條邊可使余下的n(n-1)(n-1)個CTn-2失靈。這些邊集和Sn中選取的使所有Sn-2失靈的失靈邊集構成的矩陣，在其中任意選取2列都會出現的所有組合數，并且選取的這些邊集是最優的，因此 fCT(n，2)=fS(n，2)+2n(n-1)。

引理5 對任意素數 n，fS(n，2)=3n(n-1)［11］。

由引理5和定理5可得推論1。

推論1 對任意素數n，fCT(n，2)=5n(n-1)。

引理6 當n不是素數時，fS(n，2)≤(n-1)n(p-1)，p是大于等于 n 的最小素數［9］。

由引理6和定理5可得推論2。

推論2 當n不是素數時，fCT(n，2)≤(n-1)n(p-1)+2n(n-1)，p是大于等于n的最小素數。

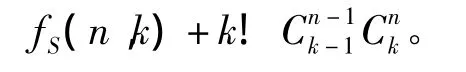
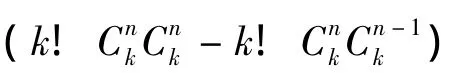
3 結束語

本文研究了在n維完全對換網絡中使每個(n-k)維子完全對換網絡失靈的失靈點和失靈邊的最小數目FCT(n，k)和 fCT(n，k)，并給出了相關結果。然而關于完全對換網絡CTn中FCT(n，k)和fCT(n，k)(2≤k≤n-3)的精確值尚未知，另外關于完全對換網絡的其它性質還有待于進一步研究。

［1］Bondy J A，Marty U S R.Graph Theory［M］.London:Springer，2008.

［2］徐俊明，組合網絡理論［M］.北京:科學出版社，2007.

［3］高隨祥.圖論與網絡流理論［M］.北京:高等教育出版社，2009.

［4］Lakshmivarahan S，Jwo J S，Dhall S K.Symmetry in interconnection networks based on Cayley graphs of permutation groups:A survey［J］.Parallel Computing，1993.19:361-407.

［5］師海忠.互連網絡的代數環模型［D］.北京:中國科學院數學與系統科學研究院應用數學研究所，1998.

［6］師海忠，路建波.關于互連網絡的幾個猜想［J］.計算機工程與應用，2008，44(31):112-115.

［7］師海忠，牛攀峰，馬繼勇，侯斐斐.互連網絡的向量圖模型［J］.運籌學學報，2011，15(3):115-123.

［8］Akers S B，krishnamurthy B.A group-theoretic model for symmetric interconnection networks［J］.IEEE Transactions on Computers，1989，38(4):555-565.

［9］Shahram Latifi，Ebrahim Saberinia，Xiaolong Wu，Robustness of star graph network under link failure［J］.Information Sciences，2008，178(3):802-806.

［10］Shahram Latifi，A study of fault tolerance in star graph［J］.Information Processing Letters，2007，102(5):196-200.

［11］David Walker，Shahram Latifi，Improving bounds on link failure tolerance of the star graph［J］.Information Sciences，2010，180(13):2571-2575.

［12］Jung-Sheng Fu，Fault-free Hamiltonian cycles in twisted cubes with conditional link faults［J］.Theoretical Computer Science，2008，407(1-3):318-329.

［13］Bernd Becker，Hans-Ulrish Simon，How robust is the ncube?［C］//Proceeding of 27th Annual Symposium on Foundations of Computer Science.［S.l.］:［s.n.］，1986:283-291.

［14］Tung-Yang Ho，Ting-Yi Sung，Lih-Hsing Hsu，Anote on edge fault tolerance with respect to hypercubes［J］.Applied Mathematics Letters，2005，18(10):1125-1128.

［15］Shiying Wang，Yuxing Yang，Fault tolerance in bubblesort graph networks［J］.Theoretical Computer Science，2012，421:62-69.