各層基礎組織互異的分形組織設計方法

馬鈴琳，張 聿

(浙江理工大學 a.材料與紡織學院;b.服裝學院，杭州310018)

隨著分形理論的日趨完善和計算機技術的不斷發展，分形理論在紡織領域的應用也越來越多［1-5］，近年來，運用分形理論進行織物組織設計也已見報道。張聿等［6-7］討論了基于L系統的圖形生成原理，借助VB編程和計算機的可視化方法研究一種基于L系統的分形組織的設計方法，張聿等［8-9］將IFS方法應用到組織設計中，使得分形組織設計不受組織點分布形式和組織循環等因素的制約，突破了L系統繪制分形組織圖的諸多局限。

但是運用上述方法繪制多層結構的分形組織圖時，都是選定一個基礎組織后進行多次組織迭代運算獲得的。本文的目的是在運用IFS方法繪制分形組織圖，基于分形幾何學中的變維數理論，通過組織矩陣的迭代運算在分形組織的不同層次嵌入不同的基礎組織，即選擇不同的基礎組織進行組織迭代運算，研究一種各層基礎組織互異的分形組織的生成方法，利用填充組織的合理配合，設計形成具有獨特結構和視覺效果的一類分形織物組織，為織物組織設計探尋新思路。

1 各層基礎組織互異的分形組織的生成方法

1.1 各層基礎組織互異的分形組織的組織結構

各層基礎組織互異的分形組織是分形組織的一種，具有多層結構，其中每一層的基礎組織的組織結構均不相同，其組織結構較為復雜。圖1為3層結構的各層基礎組織互異的分形組織，其中3×3變化平紋組織為首層基礎組織，三上一下右斜紋為次層基礎組織，四枚破斜紋為末層基礎組織。

圖1 分形組織圖1Fig.1 Fractal weave 1

1.2 各層基礎組織互異的分形組織圖的生成過程

根據IFS原理和變維數理論［10-11］，選擇不同的基礎組織，將其組織圖轉換成組織矩陣后，運用矩陣的叉積迭代運算依次進行組織矩陣的迭代，生成各層基礎組織互異的分形組織。以圖1中的組織為例，其生成過程為:

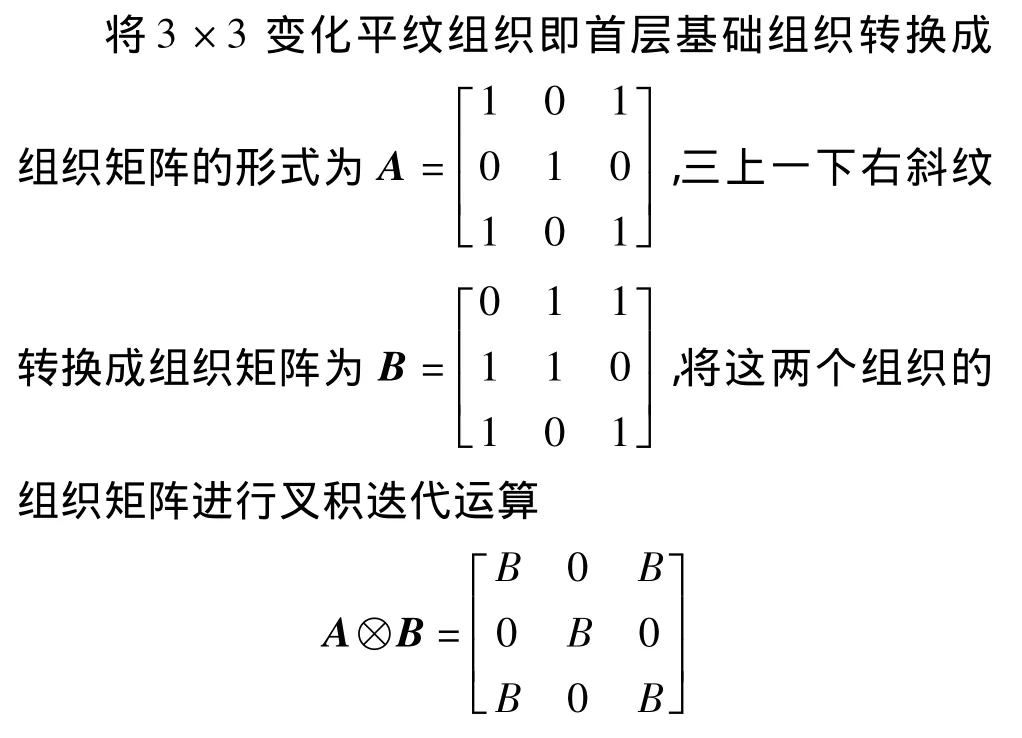
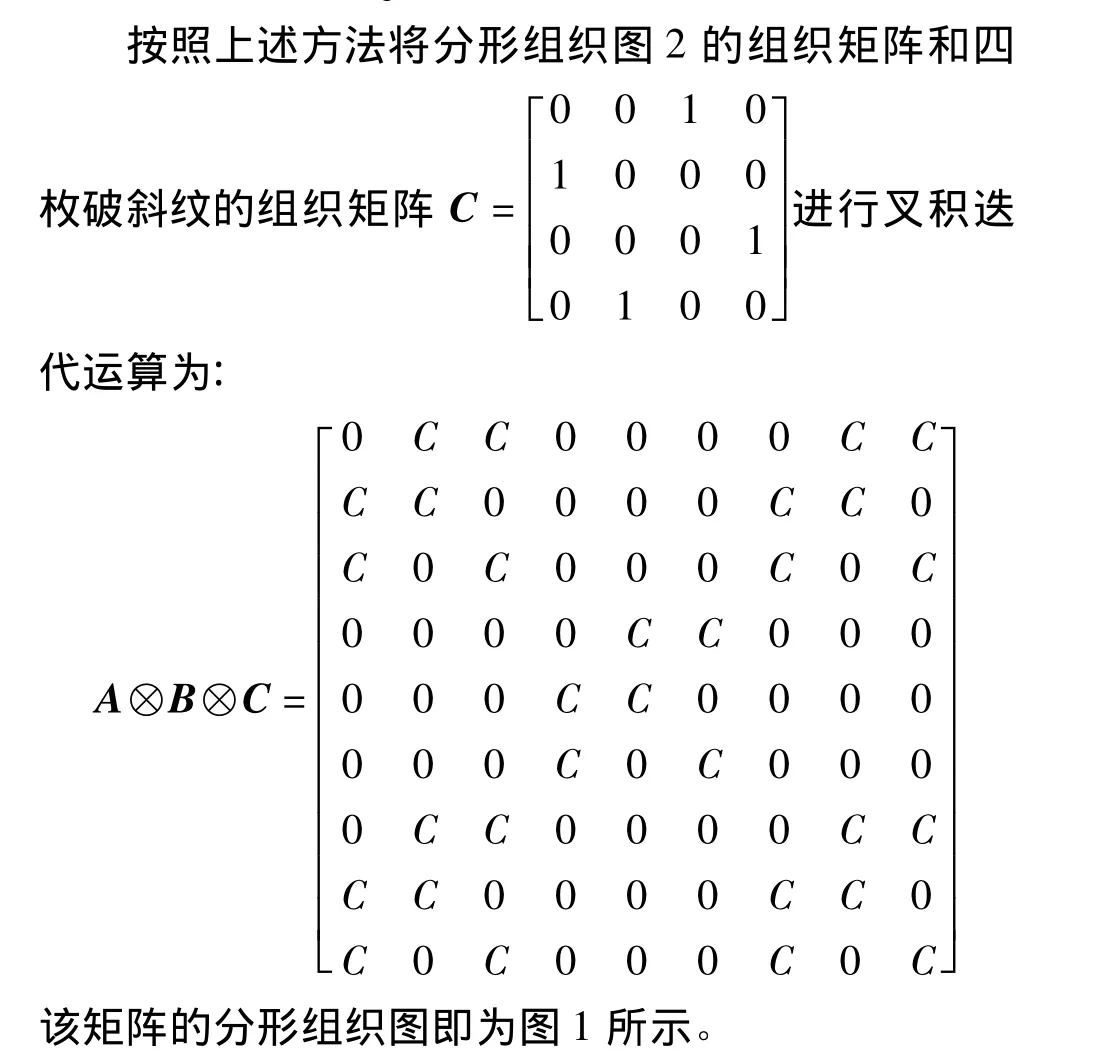
組織矩陣A中數值為0的元素與矩陣B相乘，原來的0值變為4行4列個0，數值為1的元素與B相乘，原來的數值1則被組織矩陣B中的元素代替，即按分塊矩陣的方式將三上一下右斜紋的組織矩陣B嵌入3×3變化平紋組織的組織矩陣A中元素1所在的位置，迭代后得到一個9×9矩陣，其組織圖見圖2。

圖2 分形組織圖2Fig.2 Fractal weave 2

2 各層基礎組織互異的分形組織圖的設計方法

各層基礎組織互異的分形組織圖的設計主要考慮分形層數和基礎組織兩方面。

2.1 分形層數的設計

分形層數即迭代的基礎組織的個數，應根據設計意圖和實際要求合理選擇。圖3(c)的分形層數為2，其中3×3變化平紋是首層基礎組織，四枚破斜紋是末層基礎組織，圖3(e)分形層數為3，是將五枚緯緞作為末層基礎組織嵌入到圖(c)的一級分形組織得到的。可以看出，隨著分形層數增加，分形組織圖的結構也越來越復雜。

圖3 各層基礎組織互異的分形組織設計示意圖Fig.3 Fractal weave design with different basic weave in different layer

2.2 基礎組織的設計

基礎組織是進行組織迭代時選擇的組織，根據其所在層次分為首層基礎組織，次層基礎組織，第三層基礎組織，直至末層基礎組織。各層基礎組織互異的分形組織的各個層次的組織均可是任何類型的組織，組織點的分布形式和組織循環的大小都不受限制，可以是傳統的組織如平紋、斜紋、緞紋等，也可以是非規則組織。圖4是選擇2個不同的斜紋組織作為基礎組織，迭代后得到2層結構的各層基礎組織互異的分形組織，如圖4(c)所示，圖5是選擇3個非規則組織作為各層基礎組織，迭代后獲得具有3層結構的各層基礎組織互異的分形組織，如圖5(d)所示。

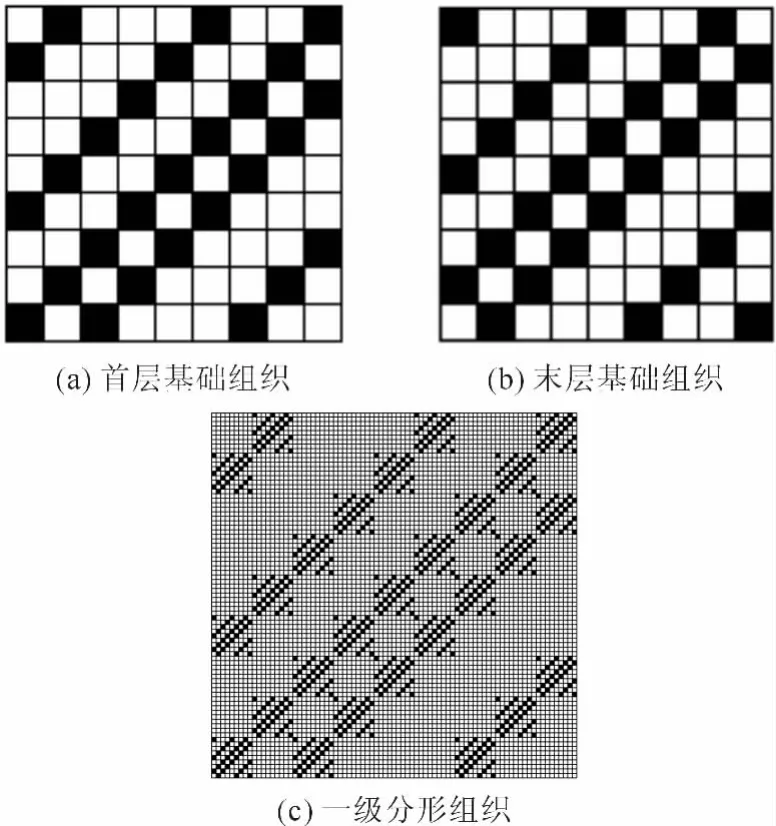
圖4 一級分形組織設計示意圖Fig.4 Fractal weave disign of the first-level

圖5 二級分形組織設計示意圖Fig.5 Fractal weave disign of the second-level

各層基礎組織互異的分形組織生成后，通過改變基礎組織的嵌入順序亦會生成風格完全不一樣的組織結構，以圖5中的二級各層基礎組織互異的分形組織為例，變化這三層基礎組織的順序，從外到里層的順序分別是圖5中的(b)(c)(a)和(c)(a)(b)，得到的分形組織如圖6中的(a)和(b)。

圖6 改變基礎組織的順序后的分形組織示意圖Fig.6 Fractal weave after basic weave sequence changed

2.3 各層基本組織互異的分形織物組織的設計方法

從各層基本組織互異的分形組織分形組織圖的生成過程來看，原來的初始組織的對象組織點被后面嵌入的組織所代替，單個的組織點隨之變成了許多個組織點的集合，原來的非對象組織點也會成為一個組織點的集合，集合中組織點均為緯組織點，導致織造時浮長過長，并且隨著分形層數的增加，浮長也隨之增大，為此，必須配合填充組織使其符合生產工藝要求。

填充組織直接影響織物成型后的肌理效果，并且隨著分形層數的增加，對織物肌理效果的影響越大，因此，同樣是生成各層基本組織互異的分形織物組織的關鍵環節。設計選擇的填充組織的組織循環數必須是末層基礎組織的組織循環數的約數，否則會出現圖形混雜的情況，其組織點分布也需考慮與末層基礎組織的配合，以免出現浮長過長的情況。此外，選擇時還必須考慮外觀方面的設計要求。圖4中各層基本組織互異的分形組織(c)為例，其末層基礎組織的完全組織循環為9，填充組織的完全組織循環可以是3和9，填充組織可以選擇變化平紋、斜紋和其他非規則組織。將圖7中的填充組織(a)的組織循環為3，與分形組織配合得到的各層基本組織互異的分形織物組織如圖7(b)所示;填充組織(c)和(e)的組織循環為9，與分形組織配合后得到的各層基本組織互異的分形織物組織如圖7(d)和(f)所示，其中(f)是選擇非規則組織作為填充組織得到的織物組織。

圖7 各層基本組織互異的分形織物組織示意圖Fig.7 Fractal weave with different basic weave in different layer

3 織造實驗結果與討論

3.1 實驗結果

各層基本組織互異的分形織物組織的特殊結構使織物產生獨特的肌理，借助紋織CAD，將圖8中所設計的各層基本組織互異的分形織物組織(a)和(c)作為素組織進行織造實驗，工藝參數設計如下:

經紗:(1/22/24.2 dtex桑蠶絲80 S捻/10 cm×2)68 Z捻/10 cm;緯紗:2/22/24.2 dtex桑蠶絲35 S捻/10 cm，設計上機經密為1150根/10 cm，緯密為900根/10 cm。

在電子提花機上織造的樣品如圖8中的(b)和(d)。

圖8 各層互異織物組織織紋效果圖Fig.8 Texture effect of fractal weave with different basic weave in different layer

將所設計的各層基本組織互異的分形織物組織應用于紋樣織造，使提花紋樣更生動。圖9中(a)為紋樣圖，紋樣經意匠處理后，在不同的色號處鋪入設計的各層基本組織互異的分形織物組織，織造后的織物實物局部效果圖如圖9(b)。

圖9 紋樣和實物Fig.9 Pattern and fabric

3.2 結果討論

從各層基本組織互異的分形織物組織的試織結果來看，織物最終的紋理效果與設計基本相符，其設計與應用可行。織物成型效果受分形層數，基礎組織和填充組織結構的影響。各層基本組織互異的分形織物組織的結構變化豐富，首先，可以通過改變分形層數來改變組織結構;其次，分形組織中每一層的基礎組織都是一個可變參數，在分形層數不變的情況下，改變任意一層的基礎組織的組織結構或者交換基礎組織的嵌入順序都能得到風格完全不同的組織;最后，配合不同的填充組織，織物結構又會截然不同。

4 結語

1)基于IFS方法和變維數理論，通過計算機可視化方法，繪制各層基本組織互異的分形組織的分形圖形，利用填充組織的合理配合，設計出具有獨特視覺效果和風格的各層基本組織互異的分形織物組織。通過織物成型實驗證明各層基本組織互異的分形組織的設計方法是現實可行的。

2)所提出的各層基本組織互異的分形織物組織是通過組織矩陣的迭代，將不同的基礎組織嵌入分形組織的不同層次，通過基礎組織和填充組織的配合變化，表現各種不同的結構和圖案效果。當分形層數增多時，各層基本組織互異的分形織物組織的復雜性和多變形也明顯增強，其組織結構很難通過織物分析來獲取，防偽性強。

3)探討各層基本組織互異的分形織物組織設計方法為織物組織設計提供了新的思路，使組織設計的空間可進一步拓展。

［1］陸振乾，錢坤.利用分形理論求解織物滲透率［J］.紡織學報，2006，27(2):17-24.LU Zhenqian，QIAN Kun.Calculate the permeability of fabric by the fractal theory［J］.Journal of Textile Research，2006，27(2):50-54.

［2］陳健敏，吳兆平，嚴灝景.分形理論在織物折皺評定中的應用［J］.中國紡織大學報，1999，25(2):34-37.CHEN Jianmin， WU Zhaoping， YAN Haojing. The application of the fractal theory in fabric wrinkle rating［J］.Journal of China Textile University，1999，25(2):34-37.

［3］張麗娟，李向紅，敖利民.分形滌綸與棉交捻紗織物的研發［J］.上海紡織科技，2010，38(5):44-47.ZHANG Lijuan，LI Xianghong，AO Limin.Development of fractal polyester and cotton cross-twist yarn fabric［J］.Shanghai Textile Science ＆ Technology，2010，38(5):44-47.

［4］萬廣蘭，于偉東.棉纖維原纖結構的分形特征［J］.紡織學報，2011，32(11):3-6.WAN Guanglan， YU Weidong. Fractal characteristic of fibrillar structure of cotton fibers［J］.Journal of Textile Research，2011，32(11):3-6.

［5］歐建文，姚金波.分形理論在羊毛紗線定形中的應用［J］.紡織學報，2011，32(5):33-37.OU Jianwen，YAO Jinbo.Fractal theory use in setting of wool yarn［J］.Journal of Textile Research，2011，32(5):33-37.

［6］張聿，金耀，孫家武，等.基于L系統的織物分形組織設計方法［J］.紡織學報，2007，28(5):50-54.ZHANG Yu，JIN Yao，SUN Jiawu，et al.The studies on designing fabric fractal-weave based on L-system［J］.Journal of Textile Research，2007，28(5):50-54.

［7］賈靜靜，張聿.基于L系統的緞紋分形組織及其織紋效果設計［J］.絲綢，2011，48(5):32-34.JIA Jingjing，ZHANG Yu.A method of designing fractal satin weave and its fabric texture based on L-system［J］.Journal of Silk，2011，48(5):32-34.

［8］雷韓，張聿.基于IFS確定性迭代算法的麥粒分形組織設計法［J］.絲綢，2012，49(8):26-28.LEI Han，ZAHNG Yu.A design method of fractal weave with barley-corn pattern based on IFS determinacy iterative algorithm［J］.Journal of Silk，2012，49(8):32-34.

［9］張聿，金耀，岑科軍.基于IFS的非規則分形組織設計方法［J］.紡織學報，2012，33(12):32-36.ZHANG Yu，JIN Yao，CEN Kejun.Method of designing irregular fractal weave based on IFS［J］.Journal of Textile Research，2012，33(12):32-36.

［10］齊旭東.分形及其計算機生成［M］.北京:科學出版社，1994.QI Xudong.Fractal and Computer Generated［M］.Beijing:Science Press，1944.

［11］FU Yuhua.Analysed and Fractal Single Point Method for Solving Hydraulic Problems in Ocean Engineering［C］.Beijing:International Meeting on Petroleum Engineering，1995.