基于神經網絡方法的Kp預報模型

劉 楊，羅冰顯，劉四清，龔建村

（1中國科學院空間科學與應用研究中心，北京100190；2中國科學院研究生院，北京100049）

1 引言

Kp指數即“行星際3h磁情指數”，通過計算磁緯在48°和63°之間的全球13個地磁臺站K指數的加權平均值得到。它與3h時段內地磁擾動有近似對數的關系，是衡量近地空間全球磁擾強度的重要指標之一。Kp指數每天8個值，從0到9共分28級：0，0+，1-，1，1+，2-，2，… ，9-，9。1949 年 Bartels利用早期的地磁觀測資料最先引入Kp指數概念，現在能獲得1932年之后長達70年無間斷Kp數據，對研究日地空間環境極具價值。與Dst和AE指數不同，Kp并沒有一個明顯的電流體系與之相對應。

統計結果表明，Kp指數與太陽風參數之間有很好的的相關性[1，2]，如太陽風速度、密度和行星際磁場的南向分量等。Kp指數同樣與近地空間的一些現象相關，如亞暴注入的位置、磁尾場線拉伸、等離子體片地向邊界和等離子體層頂的位置等[3，4]。在空間天氣應用中Kp也具有重要的作用，很多磁層和電離層模型需要Kp作為輸入參數，如Tsyganenko地磁場模型，大氣密度模型，環電流輻射帶模型和磁層頂規范預報模型等[5]，OVATION模型需要輸入Kp來確定橢圓極光帶的赤道向邊界[6]；另外可以根據估計Kp的增強對磁層電離層的粒子和電磁環境變化發布預警，能有效保護衛星和地面電力系統免受災害性的破壞。

作為全球地磁活動指數，Kp有自身的缺陷，通常最終公布的Kp會有數周的延遲，且Kp也不適用于研究較小時間尺度的問題。為了使Kp適用于實時應用的需求，一些機構發展了現報和短期預報模型。如 Gehred 等和 Takahashi等的 Kp 現報模型[7，8]，利用計算Kp的方法處理中磁緯地區幾個地磁臺站的實時數據得到Kp的估計值，雖然與最終的Kp不完全一致，但具有很好的實時性。基于人工神經網絡發展的Kp短期預報模型，主要利用上游太陽風數據和現報Kp值作為輸入參數，最早能提前幾個小時預報Kp值，主要模型有：Costello模型、Wing等的APL模型、Boberg等的和Bala等的模型[9-12]。

CME、CIR等到達地球時會引起強烈的地磁擾動，使得空間環境異常惡劣，嚴重影響人類活動和各種技術系統。雖然能實時監測太陽的爆發活動，大致預測擾動傳播到地球的時間，但太陽風與磁層電離層的相互作用是十分復雜的非線性動態過程，很難準確地預測地磁暴（Kp>5）的發生。太陽風作為驅動磁層電離層系統的主要能量來源，能量輸入的多少決定著系統的行為。利用統計方法得到的等效刻畫能量輸入的耦合函數主要有Perreault-Akasofu的ε函數 ε＝vB2l2sin4（θ/2）、Stamper等的太陽風功率函數Pα、Newell等的開磁通生成速率函數dΦMP/dt=v4/32sin8/3（θ/2）和 Borovsky 的向日面重聯率函數 εB等[13]。最近Lu.JY等用數值模擬的方法，首次定量描述了在不同太陽風條件下電磁能和動能的輸入[14]。磁層電離層對太陽風能量輸入的響應主要分為三種：直接驅動過程；加載卸載過程；兩種過程同時存在[13]。統計分析表明磁層對行星際擾動響應的時間約為1h，也存在長達幾小時至數天的響應時間，較長的響應滯后時間意味著輸入能量在磁層有存儲過程[13，15]。Johnson and Wing指出，在太陽活動高年，磁層主要受行星際條件的控制，在太陽活動低年，主要受磁層內部的動力學過程的控制，并且Kp時間序列在太陽活動低年比在高年有更顯著的非線性特性[10，16]。行星際向磁層電離層能量輸入的復雜性，磁層電離層對擾動響應時間的不確定性以及磁層內部的動力學過程，使得預報Kp指數的難度更大。

從預報地磁活動指數（Kp、Dst、AE）的準確度方面來衡量能量耦合函數，開磁通生成速率dΦMP/dt的效果最好[17]。Newell等又考慮了太陽風與磁層頂之間的粘滯作用項n1/2v2對能量輸入的貢獻，綜合開磁通生成率和粘滯作用項線性預報地磁活動指數，得到了更好的結果[18]。

人工神經網絡是模仿人類大腦的神經網絡結構和功能建立的一種信息處理系統，能夠解決高度復雜的非線性問題。目前神經網絡方法廣泛應用于空間環境預報，除了上文中提到的Kp短期預報模型外，也建立了對Dst指數、AE指數、同步軌道相對論電子通量和太陽質子事件的神經網絡預報模型[19-23]。

Kp為3h精度指數，其衡量的是這3h時段內地磁H分量變化的最大幅值，為了更好的尋找行星際擾動源與Kp之間的非線性關系，提高Kp的預報效果，把開磁通生成速率dΦMP/dt和粘滯作用項n1/2v2加入到神經網絡中來。為此，建立了三個模型以不同的方式預報未來3h內的Kp值：①模型1輸入位于L1點的ACE衛星提供的當前太陽風速度和密度，行星際磁場強度，以及開磁通生成率dΦMP/dt和粘滯作用項n1/2v2；②模型2的輸入是在模型1的基礎上加入現報Kp；③模型3輸入9h延遲dΦMP/dt的和n1/2v2，以及當前的太陽風和行星際磁場參數。

2 數據選取與處理

構建從1998年到2010年長達13年的太陽風和Kp數據集，覆蓋了幾乎整個第23太陽活動周以及24活動周的前幾年。位于L1點的ACE衛星提供了地球上游的太陽風速度密度和行星際磁場參數，這些數據來自 NASA/CDAWEB（http：//cdaweb.gsfc.nasa.gov/），開磁通生成率dΦMP/dt和粘滯作用項n1/2v2；可利用太陽風參數計算得到，最終的Kp實測值來自德國的GeoForschungsZentrum（ftp：//ftp.gfz-potsdam.de/pub/home/obs/kp-ap/），現報 Kp 來自 NOAA/SWPC（http：//www.swpc.noaa.gov/）。

本文始終是對3h時段Kp的預報，把Kp固定在每一時段結束的時間點上。將ACE衛星SWEPAM 1min精度和MAG 4min精度的數據進行30min平均，作為模型1和模型2的輸入；模型3的輸入數據的精度為3h，選取的是ACE衛星1h精度的數據，然后進行3h平均。開磁通量輸入率和粘滯作用項也相應地處理成30min和3h精度。Kp實測值幾乎是連續的，但太陽風數據存在缺失，尤其是模型3考慮了時間延遲效應，會使得有效樣本數量大大減少。

3 神經網絡的建立

BP神經網絡是一種使用誤差反向傳播學習算法的前向網絡。采用了包含輸入層、隱層和輸出層的3層BP神經網絡來預報Kp，輸入層與隱層之間采用帶偏差的對數S型激活函數，隱層和輸出層之間采用線性激活函數。將13年的數據分為兩個集合，1999-2001、2003-2005和2007-2010共10年的數據為訓練驗證集，主要用于神經網絡的訓練，尋找最優的網絡權值；1998、2002和2006年3年的數據為測試集，用于測試訓練好的網絡，評估其預報效果。測試集包含了23活動周不同階段的大量數據，以此來檢驗模型的預報能力隨太陽活動周的變化。在大量實驗的基礎上，根據不同模型的輸入樣本量，確定隱層神經元節點數量為12到20之間，訓練算法采用了具有較快收斂速度的Levenberg-Marquardt法。

對測試結果的分析主要用到以下的幾個統計參數：線性相關系數R、均方根誤差RMSE、平均相對誤差ARV，具體定義為：

其中T為目標值，即Kp實測值，O為網絡的輸出值，即Kp預報值，N代表測試樣本的總數。

4 Kp預報模型

4.1 輸入太陽風參數、dΦMP/dt和n1/2v2提前1～3.5h預報Kp：模型1

模型1的輸入參數為太陽風速度v，密度n，行星際磁場總強度B，By分量，Bz分量，開磁通生成率dΦMP/dt和粘滯作用項n1/2v2。神經網絡訓練樣本的構造過程中，把實測的3h時段Kp固定在該時段結束的時刻上，每天8個值對應的時刻分別為世界時3點，6點，……，24點。考慮到ACE衛星觀測到的太陽風傳到地球的時間以及磁層對太陽風的響應時間，假設對實測Kp值產生影響的行星際條件的時間為該時段結束前1h至4h，若t為對應的時刻（t=3UT，6UT，……，24UT），Kpt為網絡輸出的目標值，所選輸入參數的時間為t-4時刻至t-1時刻。把t-4到t-1時刻之間的3個小時平均分為六段，每段為30min，那么每一個Kp值都對應6個輸入條件組合，Kp與輸入參數的非線性關系寫成函數形式為：

其中，i=t-3.5，t-3，t-2.5，t-2，t-1.5，t-1。沒有把這 6個組合全部應用于神經網絡的訓練，而是先對其進行評估，找出可能導致地磁場產生最強擾動的一組值，作為與Kpt對應的輸入條件.這利用了Newell等提出的Kp與開磁通輸入率和粘滯作用項的線性擬合公式[18]：

分別計算6個輸入組合對應的Kplinear值，比較這6個值，選取其中Kplinear最大的一組作為最終的輸入。通過這種方法，得到10年中用于訓練和驗證的樣本數為22163。

神經網絡訓練完成之后，用包含1998年、2002年和2006年的數據進行測試。測試集的輸入同樣為30min精度，每3h時段有6組行星際條件，每一組條件輸入到神經網絡之后，輸出一個對Kpt的預測值，第一次預測在t-3.5時刻，之后每30min有一個輸出值，隨時間向前推移，最后一次預測在t-1時刻。每一次預測之后更新為網絡輸出的最大值，預測曲線始終單調上升，最終的預測值為6個預測值中最大的。測試結果表明，Kp觀測值與預測值之間的線性相關系數為0.88，均方根誤差為0.65，平均相對誤差為 0.23。圖 1給出了 1998、2002和2006年Kp實測值與預測值之間對比的散點圖，擬合曲線為y=0.77x+0.56，圖2給出的是對1998年11月和2006年12月兩次磁暴事件的預測結果。

從應用角度來看，模型1的優點是在t-3.5時刻就完成了第一次預測，即時間提前量為3.5h，表一給出了提前3.5h的對不同等級磁暴的預報效果的統計，如第一行所示，1998年、2002年和2006年共有288個時段Kp值達到5，提前3.5h能夠預報出這一變化的有93次，所占比例為33%；三年中共有10次Kp值達到8，其中有2次提前3.5h能夠預報出。

圖1 模型1預測Kp與實測Kp的對比（1998、2002、2006年）

圖2 模型1對1998年11月7日至10日、2006年12月14日至17日的兩次磁暴的預測結果

表1 模型1提前3.5h預報的結果

模型1的輸入參數均為30min精度，這樣能有效反映行星際條件的瞬時變化，保證不同情況的擾動（尤其是行星際磁場By和Bz）不會因時間的積分效應平均掉，而且大部分行星際擾動從L1點傳到地球的時間都超過30min，每隔30min對Kp進行一次預報，也能夠對即將到來強烈地磁擾動發出警告。

4.2 輸入太陽風參數、現報Kp、dΦMP/dt和n1/2v2提前1～3.5h 預報 Kp：模型 2

現報Kp是對地磁場磁擾狀態的實時估計，與最終的Kp有一定的差別，但兩者的相關性非常高，基本上能實時地反映磁層的狀態。在模型1的基礎上把現報Kp加入到神經網絡輸入中，能有效降低Kp序列的非線性效應，更加準確的預報將來的Kp。NOAA/SWPC現報Kp每3h發布一次，時段與Kp相同，約有幾分鐘的時間延遲。模型2訓練集的構造原則是在模型1選出的訓練樣本中始終加入最新的現報Kp：如果選出的太陽風條件對應的時刻為t-3.5和t-3，則輸入的是t-6時刻的現報Kp；如果選出的太陽風條件對應的時刻為t-2.5到t-1，則輸入t-3時刻的現報Kp。模型2同樣選取Kp實測值作為神經網絡訓練和測試的目標值。對測試集的測試結果為，Kp預測值與實測值的相關系數達到了0.90，均方根誤差為0.62，平均相對誤差為0.20。線性相關系數超過了模型1，并且降低了預測值與實測值的誤差。圖3給出了模型2測試集的Kp實測值與預測值之間的對比，擬合曲線為y=0.79x+0.55，圖4與圖2相同，給出了模型2對兩次磁暴事件的預測。

圖3 模型2預測Kp與實測Kp的對比（1998、2002、2006年）

圖4 模型2對1998年11月7日至10日、2006年12月14日至17日兩次磁暴的預測結果

4.3 輸入太陽風參數、dΦMP/dt和n1/2v2提前3h預報Kp：模型 3

模型3輸入當前的太陽風速度v，密度n，行星際磁場總強度B，By分量，Bz分量，以及9h延遲的dΦMP/dt和n1/2v2提前3h預報Kp。對于延遲時間的考慮，通過試驗測試了從6h到18h的不同組合，發現延遲時間超過9h，網絡的性能沒有明顯改進。若t為當前時刻，為了預測t+3時刻的Kp，把模型的輸入與輸出寫成函數表達式為：

網絡訓練完成之后，利用模型3對測試集的數據進行測試，結果表明Kp預測值與實測值的相關系數為0.85，均方根誤差為0.72，平均相對誤差為0.27。與前兩個模型相比，預報時間提前，所付出的代價是各項統計指標均變差。圖5給出了預測值與實測值的對比，圖6是對1998年11月和2006年12月兩次事件的預測結果。

4.4 Kp模型的預報效果

從2002年的數據中隨機選取了50d做測試，這段時間包含了三次較強的磁暴過程。圖7給出了測試結果，（a）、（b）和（c）表示對應的太陽風條件，（d）、（e）和（f）分別為模型1、模型2和模型3的輸出與實測Kp的對比。三個模型的預測曲線與太陽風條件有很好的對應關系，當行星際源發生劇烈擾動時，預測Kp明顯上升。模型1和2基本上準確的預報出了磁暴（Kp>5）的發生，模型3因為提前時間更長的原因，結果偏低。

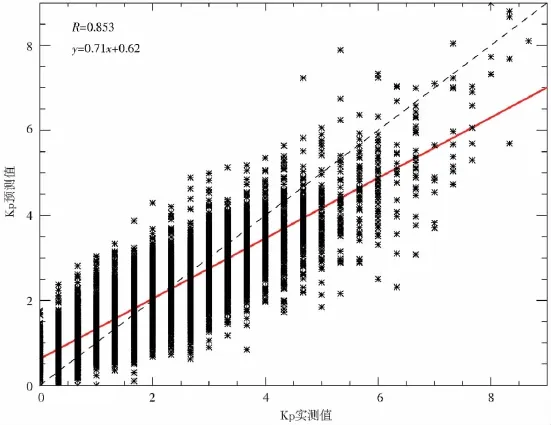
圖5 模型3預測Kp與實測Kp的對比（1998、2002、2006年）

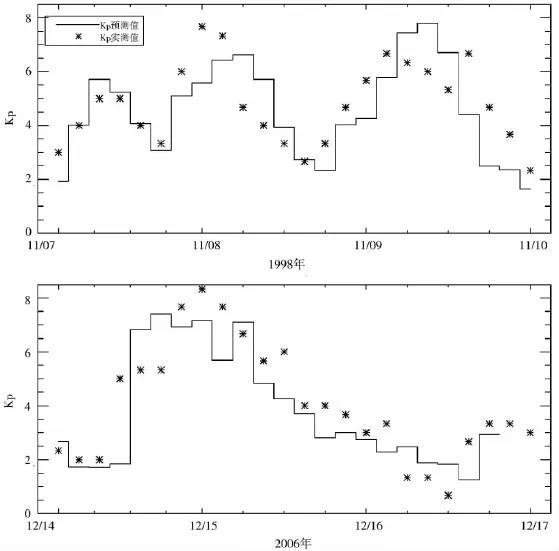
圖6 模型3對1998年11月7日至10日、2006年12月14日至17日的兩次磁暴的預測結果

圖7 從2002年隨機選取的50d的測試結果，（a）-（c）分別為行星際磁場總強度、By及Bz分量，太陽風速度和密度（d）-（e）中黑色線為Kp實測值，紅色線分別表示三個模型的預測值

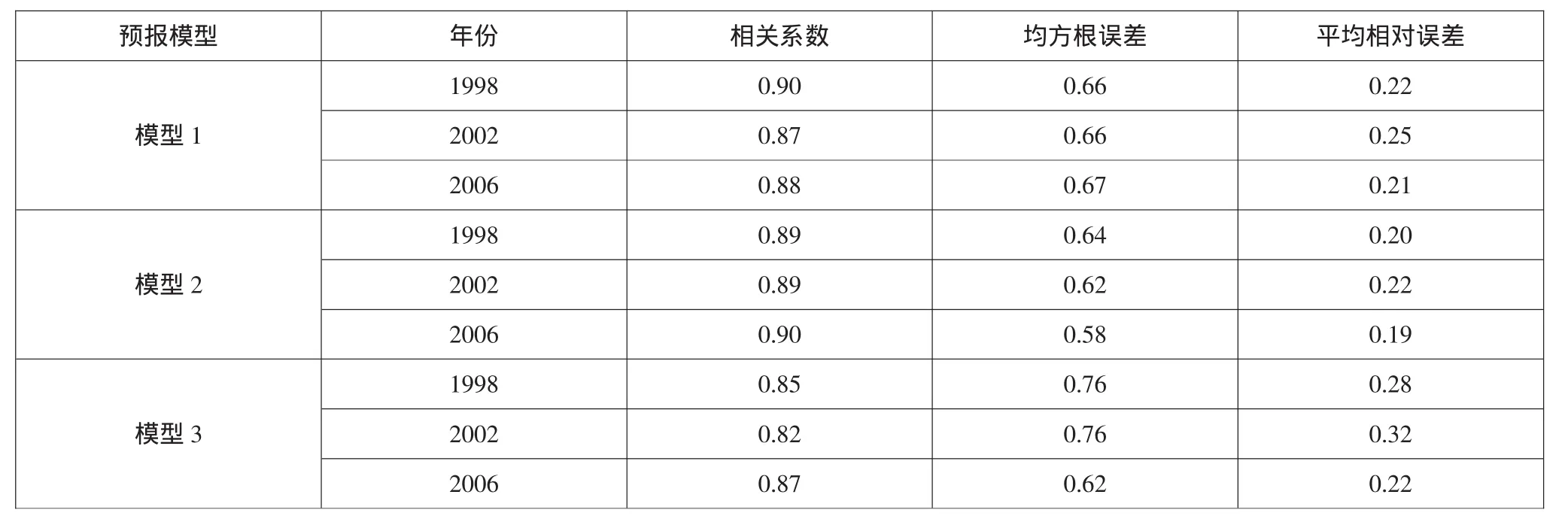
表2 三個模型在不同年份中的統計特性

表2列出了三個模型對不同年份數據的測試結果，從表2中可以看出，同一個模型在太陽活動低年的表現優于高年；不同模型在2006年的各項指標幾乎一致，這與太陽活動低年地磁平靜，Kp指數維持在較低水平有關，2002年的測試結果則顯示模型1和2明顯好于模型3。

5 討論與結論

為了滿足空間環境預報的需要，發展了三個不同的Kp指數短期預報模型，利用開磁通生成率和太陽風磁層粘滯作用項與Kp之間較強的線性相關性，把這兩個參數同ACE衛星直接觀測到的太陽風參數一起加入到神經網絡中來，訓練神經網絡，尋找行星際條件與地磁擾動之間的非線性關系。

模型1和模型3的輸入只與太陽風參數有關，模型2需要輸入反映最新磁層狀態的現報Kp值。模型1和模型2通過對每一Kp時段的六組行星際條件進行評估，找到可能產生最強磁擾的一組條件，巧妙地構造了神經網絡訓練集。測試結果表明，模型1和模型2實際預報的平均時間提前量約為2.5h，對Kp>5事件預報的平均提前時間也是2.5h，兩者有很好的一致性。

通過對隨機選取的磁暴事件進行測試，可以看出模型1在磁暴的起始階段能準確地預測Kp指數的迅速增加，預測的磁暴強度與實測值符合得很好，但由于模型1輸入的太陽風參數的積分時間較短且完全假設磁暴由行星際擾動所驅動，可能會導致磁暴恢復相期間對Kp預報值偏低，持續性較差。總的來說，模型1對響應時間較短、能量釋放迅速的磁暴預測較好，這也是大部分僅以較短時間延遲的行星際參數為輸入預報Kp模型的特點。

模型2加入了現報Kp，提高了對磁暴恢復相以及太陽活動低年由磁層內部活動引發的磁暴的預報能力，從圖3、圖4和圖7（e）中可以看出現報Kp對模型1的改進。模型3增加了開磁通輸入率和粘滯作用項的延遲時間，增大了預報的提前時間量，但圖7（f）顯示了Kp預測曲線與實測結果有一定的滯后時間。

為了更好地評估站點模型，表3列出了主要的基于神經網絡方法的Kp預報模型和具體參數[9-12]。表3中列出的模型根據輸入量的不同主要可分為兩類：第一類是完全輸入上游太陽風參數，第二類同時輸入地磁參量（實時Kp估計值）與太陽風參數。通過比較這兩類模型的相關系數和均方根誤差，可以看到加入Kp估計值能提高Kp的預報精度。根據業務需求和輸入量構造方式的不同，所有模型的時間提前量從1h到4h不等，其中APL模型的提前時間是通過計算太陽風從L1點傳播到磁層頂的時間得到的，本文的模型能從提前3.5h至1h連續的對某一時段內的Kp做出預測。比較本文模型1，APL 3和Bala的Model 3得到，開磁通生成率和粘粘滯作用項的加入提高了預報精度，直接輸入的太陽風參數也起到了重要作用。APL 1由于輸入了15min精度的Kp估計值，取得了更好的效果，本文的模型2受3h Kp估計值的限制，結果稍差，但均方根誤差明顯低于Bala的Model 1和Model 2。總之，受益于ACE衛星提供的幾乎覆蓋第23活動周的數據，以及太陽風磁層能量耦合函數的引入，本文的三個模型都取得了很好的預報效果。◇

表3 本文的模型與現有模型的比較

［1］Crooker N U，Gringauz K I.On the low correlation between longterm averages of solar wind speed and geomagnetic event activity after 1976.J Geophys.Res.1993，98.59

［2］Papitashvili V O，Papitashvili N E，King J H.Solar cycle effects in planetary geomagnetic activity：Analysis of 36-year long OMNI dataset.Geophys.Res.Lett.2000，27，2797-2800

［3］Wing S，Newell P T，Sibeck D G，et al.Large statistical study of the entry of interplanetary

magnetic field Y-component into the magnetosphere.Geophys.Res.Lett.1995，22，2086-2086

［4］Sergeev V A，Malkov L，Mirsula K.Testing the isotropic boundary algorithm method to evaluate the magnetic field configuration in the tail.J Geophy.Res.1993，98，7609-7620

［5］Detman T，Joselyn J A.Real-time Kp predictions from ACE real time solar wind.AIP Conf.Proc.1999，471，729-732

［6］Newell P T，Sotirellis T，Carbary J F，et al.OVATION：Oval Variation， Assessment， Tracking， Intensity， and Online Nowcasting.Ann.Geophys.2002，20，1039-1047

［7］Gehred P A，Cliffswallow W，Schroeder J D.A comparison of USAF Ap and Kp indices and Gottingen indices.Tech.Memo.ERLSEL，NOAA，Silver Spring，Md.1995

［8］Takahashi K，Toth B A，Olson J V.An automated procedure for near-real-time Kp estimates.J Geophy.Res.2001，106：21-017

［9］Costello K A.Moving the Rice MSFM into a real-time forecast mode using the solar wind driven forecast mode.PHD dissertation，Huston，Texas，Rice Univ，1997

［10］Wing S，Johnson J R，Jen J，et al.Kp forecast model.J Geophy.Res.2005，110，A04203，doi：10.1029/2004JA010500

［11］Boberg F，Wintoft P，Lundstedt H.Real time Kp prediction from solar wind data using neural networks.Phys.Chem.Earth.2000，25，275-280

［12］Bala R，Reiff P H，Landivar J E.Real-time prediction of magnetosphere activity using the Boyle Index.Space Weather，2009，7，S04003，doi：10.1029/2008SW000407

［13］徐文耀.太陽風-磁層-電離層耦合過程中的能量支出.空間科學學報，2011，31(1)：1～14

［14］Lu J Y，Jing H，Liu Z Q，Kabin K，and Jiang Y，Energy transfer across the magnetopause for northward and southward interplanetary magnetic fields，J Geophy.Res.，doi：10.1002/jgra.50093

［15］Bargatze L F， BarkerD N， McPherron R L， etal.Magnetospheric impulse response for many levels of geomagnetic activity.J Geophy.Res.，1985.90(A7)：6387-6394

［16］Johnson J R，Wing S.A solar cycle dependence of nonlinearity of magnetospheric activity.J Geophy.Res.2005，110，A04211，doi：10.1029/2004JA010638

［17］Newell P T，Sotirelis T，Liou K，et al.A nearly universal solar wind-magnetosphere coupling function inferred from 10 magnetospheric state variables.J Geophy.Res.2007， 112，A01206，doi：10.1029/200JA012015

［18］Newell P T，Sotirellis T，Liou K，et al.Pairs of solar windmagnetosphere coupling function：Combining a merging term with a viscous term work best.J Geophy.Res.2008，113，A04218，doi：10.1029/2007JA012825

［19］Wu J G，Reiff P H.Geomagnetic storm predictions fron solar wind data with the use of neural networks.J Geophy.Res.1997，102，255

［20］Wu J G，Lundstedt H.Geomagnetic storm predictions from solar wind data with the use of dynamic neural networks.1997，102，14255-14268

［21］Gleisner H，Lundstedt H.Response of the auroral electrojets to the solar wind modeled with neural networks.J Geophy.Res.1997，102，14269-14278

［22］龔建村，薛炳森，劉四清等.神經網絡方法在太陽質子事件短期預報中的應用.空間科學學報，2003，23(6)：443～451

［23］ PerryK L， GinetG P， LingA G， etal.Comparing geosynchronous relativistic electron prediction models.Space Weather，2010，8，S12002，doi：10.1029/2010SW000581