空間站對接碰撞能量計(jì)算的簡化分析

肖余之，時(shí)軍委，胡雪平

（1國防科技大學(xué)航天科學(xué)與工程學(xué)院，長沙410073；2上海市空間飛行器機(jī)構(gòu)重點(diǎn)實(shí)驗(yàn)室，上海201108）

1 引言

隨著我國載人航天技術(shù)的持續(xù)發(fā)展，建立空間站已成為下一步的任務(wù)目標(biāo)。國外的空間站建立較早，主要有俄羅斯/前蘇聯(lián)的“禮炮”號系列空間站、“和平”號（MIR）空間站，美國的“天空實(shí)驗(yàn)室”，歐洲航天局的空間實(shí)驗(yàn)室（Spacelab），以及由美、俄、日、歐洲等16國及地區(qū)組織共同建設(shè)的國際空間站（ISS），這些空間站的建造和運(yùn)營過程中都使用了交會(huì)對接技術(shù)[1]。對接機(jī)構(gòu)可以分為錐桿式和周邊式，錐桿式碰撞能量的計(jì)算相對簡單，由于周邊式幾何構(gòu)型復(fù)雜，其碰撞能量的計(jì)算十分復(fù)雜，傳統(tǒng)方法都是通過數(shù)值積分解決。

未來我國空間站從“I”字構(gòu)型變?yōu)椤癓”字構(gòu)型再變成“T”字構(gòu)型的建造過程中，以及載人飛船和貨運(yùn)飛船來訪的運(yùn)營過程中都需要通過-V-Bar對接完成。對接過程是典型的動(dòng)力學(xué)[2]過程，兩航天器以一定的相對速度接近，直到主、被動(dòng)對接機(jī)構(gòu)的對接環(huán)相互碰撞、捕獲，然后緩沖相對運(yùn)動(dòng)的能量。對接機(jī)構(gòu)的緩沖系統(tǒng)必須在確保捕獲的前提下在有限位移和轉(zhuǎn)角內(nèi)緩沖并消耗掉碰撞產(chǎn)生的能量，使得兩航天器相對運(yùn)動(dòng)停止并對準(zhǔn)，為拉近和剛性連接做好準(zhǔn)備。

對接碰撞的能量除與對接初始條件相關(guān)外，還與對接航天器的質(zhì)量、慣量以及航天器是否存在偏心有關(guān)。在天宮一號與神舟八號對接時(shí)兩個(gè)航天器噸位比較接近，而空間站對接時(shí)目標(biāo)航天器的噸位、慣量以及構(gòu)型都有比較大的變化。比如空間站為“I”字構(gòu)型時(shí)對接，碰撞能量主要集中在對接機(jī)構(gòu)的軸向，其它方向相對較小；空間站為“L”構(gòu)型時(shí)，由于偏心的原因?qū)⑹沟幂S向碰撞引起空間站的旋轉(zhuǎn)，軸向能量向偏轉(zhuǎn)方向有能量轉(zhuǎn)化，使得偏轉(zhuǎn)方向上的能量增加很多；空間站為“T”字構(gòu)型時(shí)，由于其慣量增加很多也會(huì)導(dǎo)致碰撞能量上升。根據(jù)空間站的建造和運(yùn)營過程中的對接需求，對各種對接碰撞產(chǎn)生的能量進(jìn)行計(jì)算，并根據(jù)對接機(jī)構(gòu)的適應(yīng)能力進(jìn)行方案的選擇。

本文就任意兩航天器的碰撞式空間對接，建立了三維等效模型來計(jì)算碰撞產(chǎn)生的能量，并根據(jù)空間站構(gòu)型將三維模型合理簡化成二維模型，并對空間站“I”字、“L”字以及“T”字構(gòu)型時(shí)的對接碰撞能量進(jìn)行了分析。二維模型能夠直觀、方便、快速的計(jì)算空間站對接過程中碰撞產(chǎn)生的能量。

2 三維模型

航天器的對接撞擊發(fā)生在很小的區(qū)域，因此可以把兩個(gè)航天器看成除相互碰撞點(diǎn)外都是剛性體的撞擊過程[3]。如圖1，分析兩個(gè)質(zhì)量、轉(zhuǎn)動(dòng)慣量和質(zhì)心分別為mi和Ii和oi（i=1，2）剛體的撞擊過程。坐標(biāo)系oxyz為地心慣性坐標(biāo)系，o1x1y1z1和o2x2y2z2分別為兩航天器的本體坐標(biāo)系，坐標(biāo)軸為航天器的慣性主軸。

兩航天器的平動(dòng)和轉(zhuǎn)動(dòng)方程為，

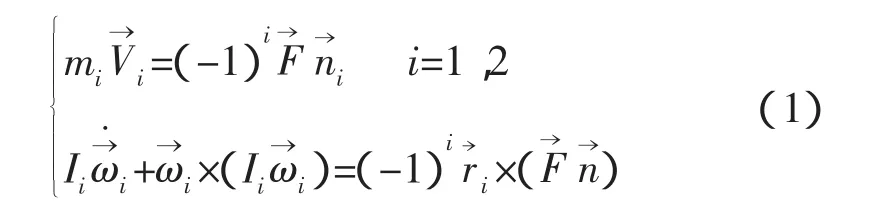
兩個(gè)剛體的運(yùn)動(dòng)方程由碰撞點(diǎn)的聯(lián)系方程關(guān)聯(lián)。聯(lián)系方程為：相互接觸點(diǎn)的速度之和與對接機(jī)構(gòu)在接觸點(diǎn)沿公法線方向的投影和相等[2]，即

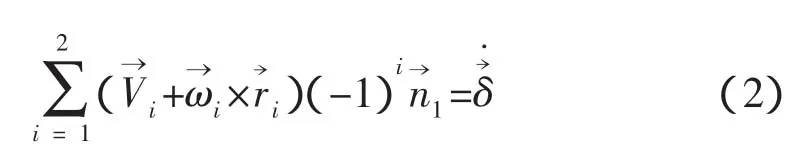
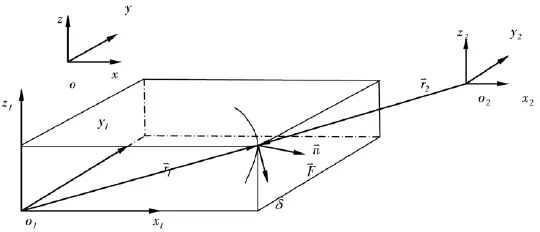
圖1 兩航天器相互碰撞示意圖

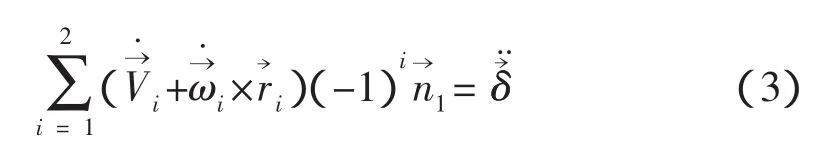
將動(dòng)力學(xué)式（1）代入上式得，

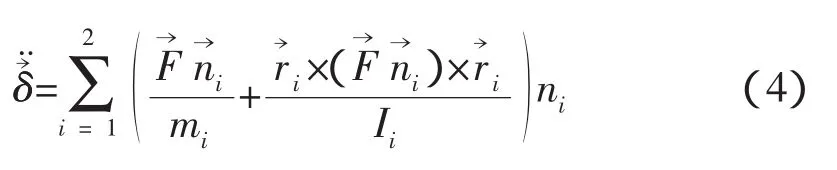
上式即為等效的動(dòng)力學(xué)方程，這樣就把兩對接航天器的相對運(yùn)動(dòng)和碰撞問題簡化為一個(gè)具有等效質(zhì)量、慣量的物體與一個(gè)僅有幾何形狀的固定障礙物的撞擊。對應(yīng)的等效質(zhì)量為mδ，

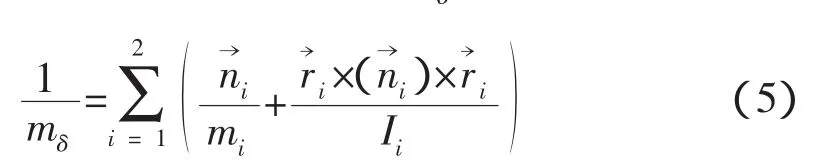
異體同構(gòu)對接機(jī)構(gòu)有22種接觸情況[4]，即使在簡化的情況下分析也是復(fù)雜的，通常需要通過求解式（4）的常微分方程才能給出準(zhǔn)確的碰撞能量。空間站對接時(shí)，航天器的噸位比較大，式（5）的等效質(zhì)量主要取決于航天器的質(zhì)量、慣量和質(zhì)心位置矢量，可以根據(jù)空間站航天器的特點(diǎn)做進(jìn)一步的簡化。

3 平面模型

3.1 等效模型的建立

如圖2所示，坐標(biāo)系oxyz為慣性坐標(biāo)系，o1x1y1z1和o2x2y2z2分別為兩航天器的本體坐標(biāo)系，坐標(biāo)軸為物體的慣性主軸，o3x3y3z3表示主動(dòng)對接機(jī)構(gòu)安裝坐標(biāo)系，其中o3位于主動(dòng)對接機(jī)構(gòu)在航天器的安裝點(diǎn)。航天器i在平面內(nèi)轉(zhuǎn)過的角度為θi；矢量與水平方向的夾角為αi，與航天器i軸線的夾角為βi。根據(jù)幾何關(guān)系有，

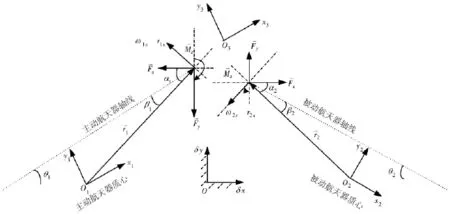
圖2 平面模型圖

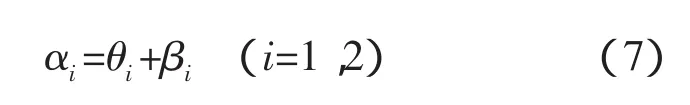
兩航天器的平動(dòng)和轉(zhuǎn)動(dòng)方程（1）式在圖2的平面情況下為，

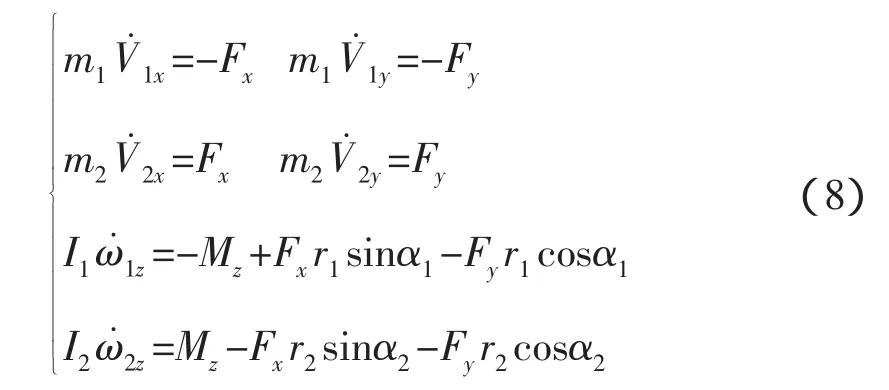
這時(shí)接觸點(diǎn)的聯(lián)系方程式（2）為，

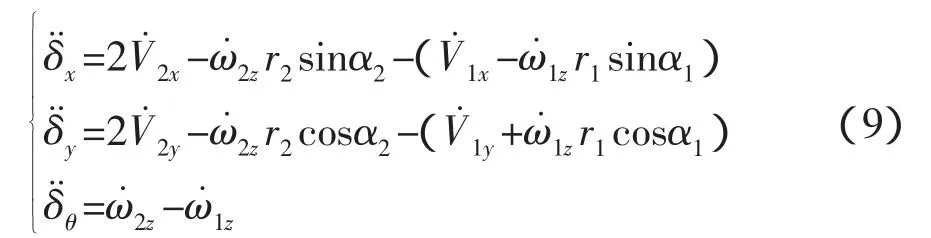
考慮初始條件范圍內(nèi)（θ1，2≤5°），cosθ1≈1 聯(lián)系方程式（9）投影到o3x3y3z3坐標(biāo)系為

將動(dòng)力學(xué)方程式（8）代入上式并整理得，

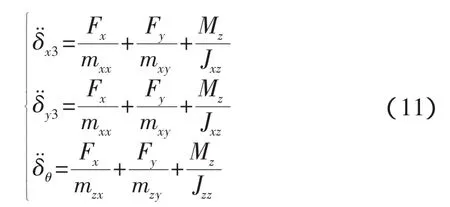
由于對接環(huán)的質(zhì)量遠(yuǎn)遠(yuǎn)小于航天器的質(zhì)量，其慣性對碰撞力的貢獻(xiàn)可以忽略[2]，并利用初始條件范圍內(nèi)cosθ1≈1，則緩沖系統(tǒng)力可以寫成碰撞與速度的函數(shù)，具體如下，

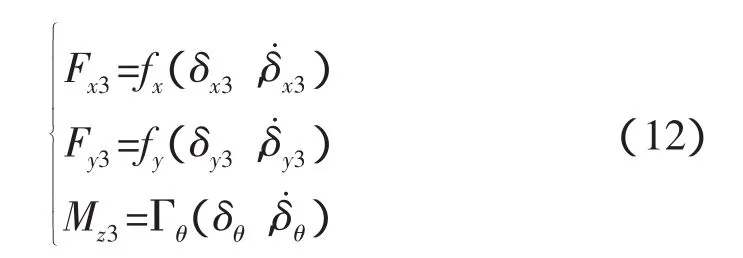
將上式代入式（11），即可得到對接環(huán)在O3系的動(dòng)力學(xué)方程，

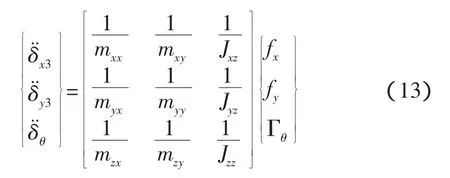
上式中各系數(shù)項(xiàng)即為等效質(zhì)量、等效慣量，具體如下：

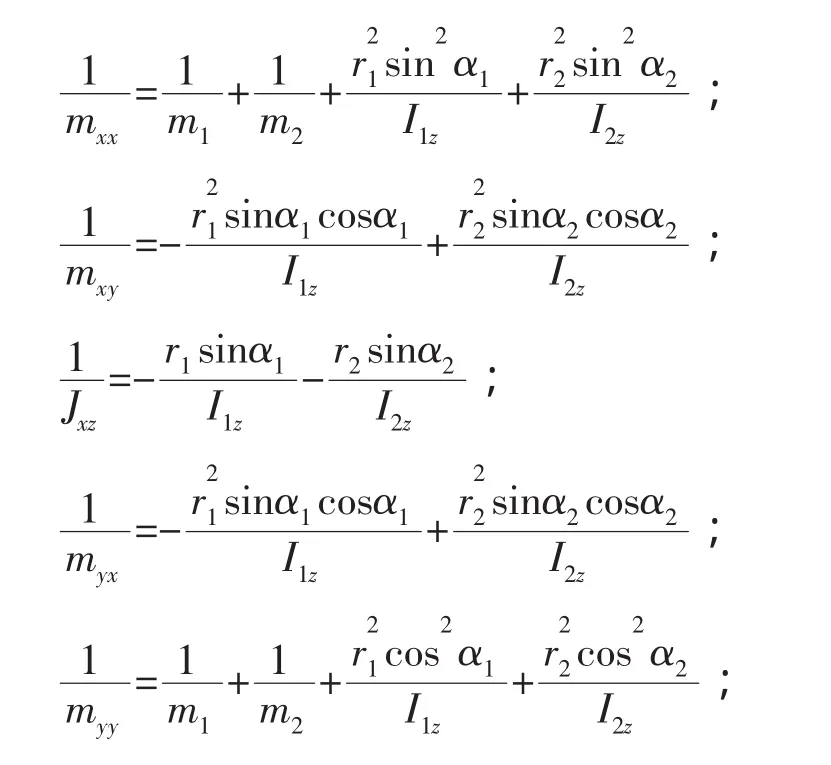
系數(shù)間有如下等式成立，證明（13）式中的等效質(zhì)量陣為對稱矩陣。

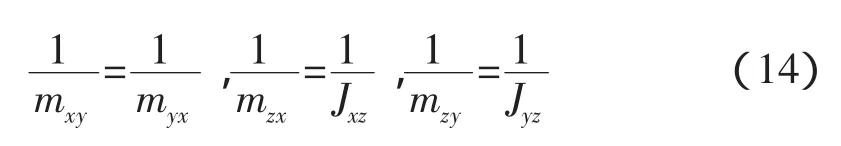
式（13）是一個(gè)基本的等效模型，在這個(gè)模型的基礎(chǔ)上可以得到縱向、橫向以及偏轉(zhuǎn)方向緩沖模型的一些特點(diǎn)。

比如縱向等效質(zhì)量mxx，航天器質(zhì)心在其軸線上（βi=0）時(shí)的正碰（θi=0）情況下這與文獻(xiàn)［5］的結(jié)果一致，具體為

如圖3所示，主動(dòng)航天器為“I”字構(gòu)型飛船（α1=0），空間站為“L”字構(gòu)型的正碰對接時(shí)，縱向等效質(zhì)量為

圖3 空間站L構(gòu)型對接示意圖

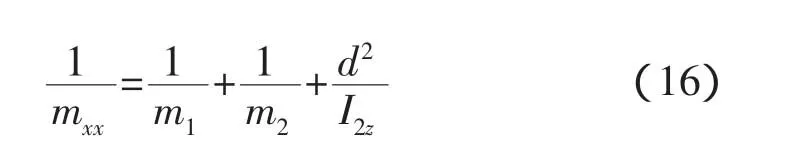
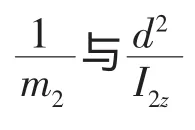
偏轉(zhuǎn)方向的方程可以通過（13）式消去fx和fy得到，

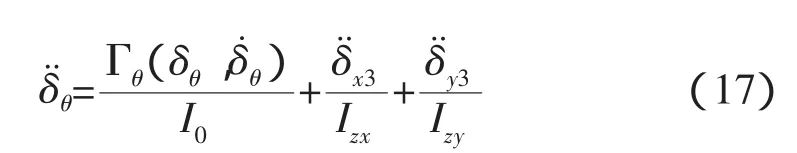
偏轉(zhuǎn)方向的等效慣量I0如下式。

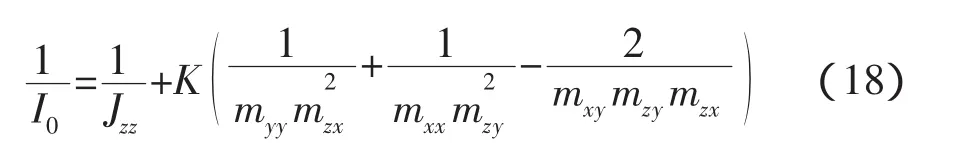
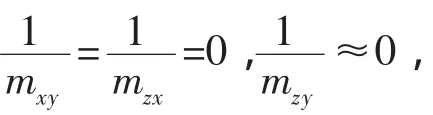
“L”構(gòu)型的對接，式（18）中的各項(xiàng)都不為零，偏轉(zhuǎn)方向的等效慣量與兩個(gè)航天器的質(zhì)量、慣量以及質(zhì)心位置都有耦合，這恰好體現(xiàn)了偏心對接的復(fù)雜性。

3.2 初始條件的模型

按照式（6）求解碰撞能量還需要知道速度和角速度的初始值。對于周邊式對接機(jī)構(gòu)來說，捕獲后的緩沖過程中縱向和滾轉(zhuǎn)方向的運(yùn)動(dòng)衰減時(shí)間約幾秒；橫向運(yùn)動(dòng)的衰減時(shí)間約十幾秒；而偏轉(zhuǎn)方向的衰減時(shí)間長達(dá)幾十秒乃至幾分鐘的量級。捕獲后航天器相對角速度對大噸位或偏心對接來說是很重要的，假設(shè)縱向和橫向分別受到?jīng)_量Nx和Ny作用并忽略力矩引起的沖量，根據(jù)動(dòng)量守恒初始速度和變?yōu)榱愕臈l件為，

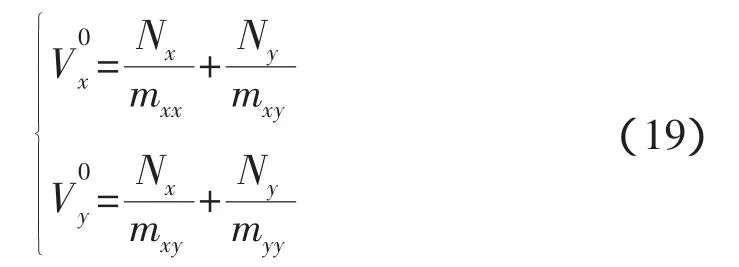
上式經(jīng)整理可以求出沖量Nx和Ny，

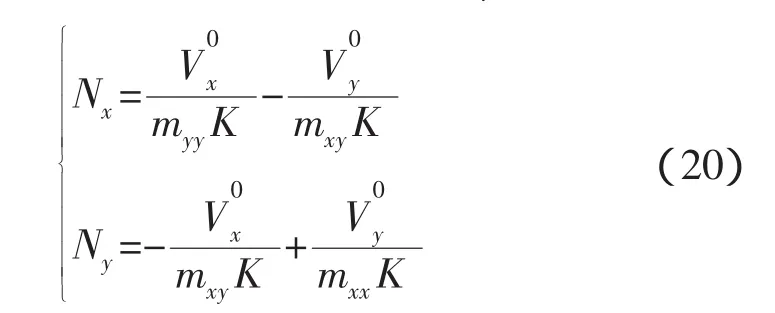
根據(jù)沖量Nx和Ny的作用，就可以計(jì)算捕獲后的相對角速度，

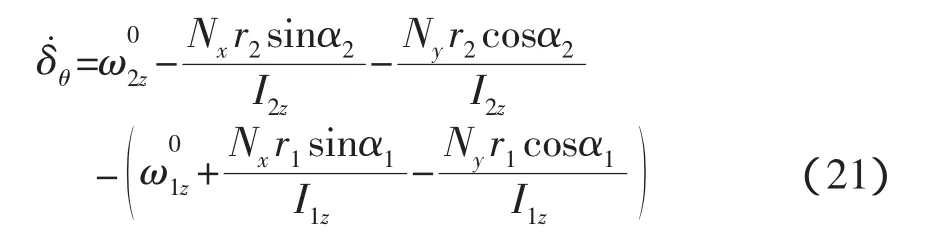
上式經(jīng)整理后得，

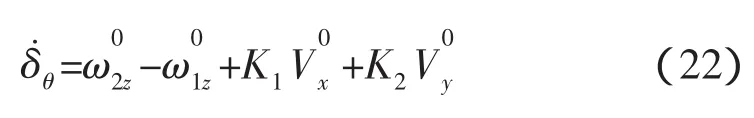
式中系數(shù)分別如下，

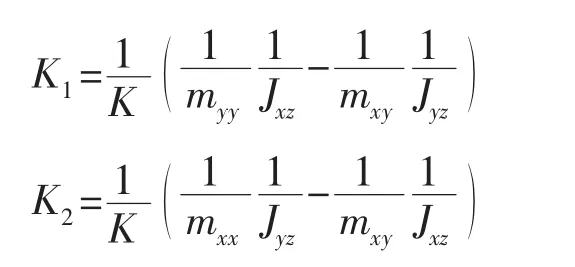
這樣結(jié)合式（18）就可以對偏轉(zhuǎn)能量進(jìn)行分析。

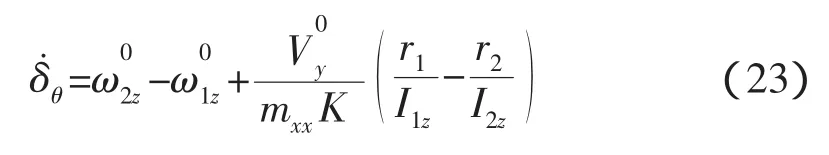
從上式可以看出，同軸對接，縱向沖擊不引起偏轉(zhuǎn)角速度，但側(cè)向撞擊引起的角速度在目標(biāo)航天器的質(zhì)心距離對接面比較遠(yuǎn)時(shí)是不可忽視的，也就是說如果目標(biāo)航天器是細(xì)長的‘I’字構(gòu)型，要特別注意控制橫向速度。

再來討論圖3中“L”構(gòu)型的同軸偏心對接，有β1＝0，且θ1＝0；目標(biāo)初始轉(zhuǎn)角為零θ2＝0，α2=β2。將這些條件代入式（13）的系數(shù)中重新求式（22），不考慮航天器的初始角速度，僅研究軸向和橫向撞擊引起的旋轉(zhuǎn)為，

通過式（24）可以分別對軸向撞擊或橫向撞擊引起的偏轉(zhuǎn)速度進(jìn)行分析。式（24）分為兩項(xiàng)，前一項(xiàng)為軸向撞擊引起的偏轉(zhuǎn)，與偏心量r2y很相關(guān)，與主動(dòng)航天器的慣量無關(guān)；后一項(xiàng)為橫向撞擊引起的偏轉(zhuǎn)，與偏心量r2y無關(guān)。結(jié)合圖3和式（24），軸向撞擊引起的偏轉(zhuǎn)角速度總是為負(fù)，只有在為負(fù)號時(shí)兩者才可以疊加求得最大值，這與對接試驗(yàn)中的現(xiàn)象是一致的。

4 計(jì)算分析

有了縱向和橫向的初始速度和角速度、等效質(zhì)量和慣量就可以進(jìn)行捕獲后的分析。航天器“L”構(gòu)型的質(zhì)量和機(jī)構(gòu)的特性分別按文獻(xiàn)6、7進(jìn)行算例分析，計(jì)算結(jié)果如下。

（1）軸向撞擊引起的角速度為1.0°/s；橫向撞擊引起的角速度為 1.4°/s，兩者之和為 2.4°/s，該值是航天器相對偏航初始角速度的3倍。可見在偏心情況下，無論是軸向撞擊引起的偏轉(zhuǎn)角速度，還是橫向撞擊引起的偏轉(zhuǎn)角速度都是不可忽略的。

（2）如圖4所示，為機(jī)構(gòu)偏轉(zhuǎn)緩沖能量與空間站對接碰撞能量消耗需求關(guān)系。空間站各種構(gòu)型對接碰撞產(chǎn)生的能量在20J～200J之間，遠(yuǎn)超過機(jī)構(gòu)40J的承受極限，當(dāng)空間站的構(gòu)型與質(zhì)量特性已定時(shí)，降低軸向速度和橫向速度是降低碰撞能量有效措施。

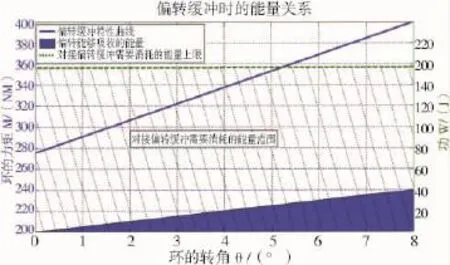
圖4 偏轉(zhuǎn)緩沖時(shí)的能量關(guān)系

5 結(jié)論

本文就任意兩航天器碰撞式對接，建立三維等效模型計(jì)算碰撞能量，根據(jù)空間站構(gòu)型將三維模型合理簡化成二維模型，二維模型無需求解常微分方程，并對空間站“I”字、“L”字構(gòu)型以及“T”字構(gòu)型時(shí)的對接碰撞能量進(jìn)行了分析。簡化模型能夠直觀、方便、快速地計(jì)算對接碰撞產(chǎn)生的能量。◇

［1］林來興.自主空間交會(huì)對接技術(shù)進(jìn)展.載人航天，2005，（4）：13-17.

［2］婁漢文，曲廣吉，劉濟(jì)生.空間對接機(jī)構(gòu).航天工業(yè)出版社1992.

［3］ W.J.Stronge，Impact Mechanics，Cambridge University Press 2000.

［4］王興貴等，周邊式對接機(jī)構(gòu)的航天器首次接觸撞擊點(diǎn)的確定宇航學(xué)報(bào)，1999，1（1）：50-57.

［5］洪嘉振.計(jì)算多體系統(tǒng)動(dòng)力學(xué).高等教育出版社，1999.

［6］張崇峰，肖余之等.航天器對接機(jī)構(gòu)緩沖器的設(shè)計(jì)研究，哈爾濱工業(yè)大學(xué)學(xué)報(bào)，1998，30（5）：112-115.

［7］李廣興，肖余之等.空間站組裝過程姿態(tài)控制方案研究，載人航天.2012，18（1）：22：29.

［8］趙陽，曹喜濱等.空間對接機(jī)構(gòu)緩沖元件吸能分配，振動(dòng)工程學(xué)報(bào)，2000，13（3）：439：442.